数学文化:高考怎么考,考生怎么答
史嘉
2016年9月,教育部考试中心下发《关于2017年普通高考考试大纲修订内容的通知》,公布了2017年普通高考各科考试大纲修订内容,数学学科与前两年悄悄地考查数学文化不同的是,这次高调通知“在能力要求内涵方面……增加了数学文化的要求”.果真,数学文化内容的考查在2017年的课标I、Ⅱ卷中均有体现,今后的高考试卷中也会成为常客.
可见,高考“考查”数学文化将是常态.但是可以命制高考试题的数学文化素材(如数学古籍、数学史料等)浩如烟海,同学们普遍感到备考束手无策.考生们又该如何备考、答题呢?我们先梳理近三年课标卷中的数学文化试题,看看高考是怎么考的,
一、数学文化高考试题
什么是数学文化高考试题,没有明确的权威的概念界定,这里主要列举以数学史料为背景的考题.
从以上统计看,课标卷已经将考查数学文化作为“规定动作”,且均以选择题形式考查中国古代数学取得的成就.
二、对比欣赏数学文化高考试题
我们来一起看看这类试题具体是以怎样的角度和形式考查的,对我们解答此类试题又有怎样的影响.
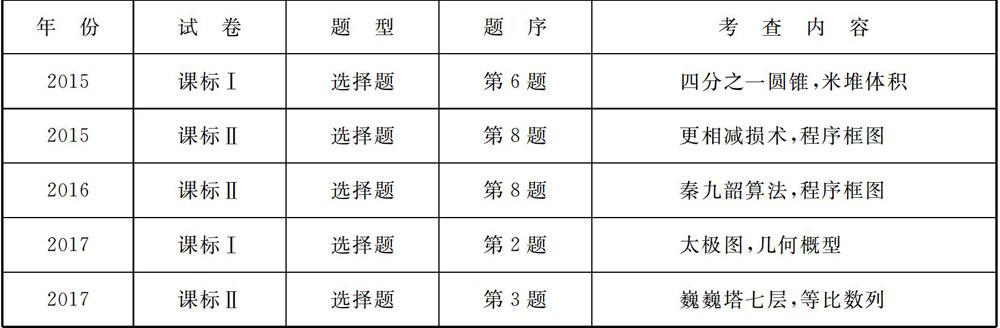
试题1 (2015年课标工卷第6题)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图1,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有()
A. 14斛
B.22斛
C.36斛
D. 66斛
仔细审题,发现该题就是在米堆和古代度量单位的背景下考查计算四分之一圆锥(给出弧长和高)的体积(或者说容积).从思维量和计算量看应该属于简单题.
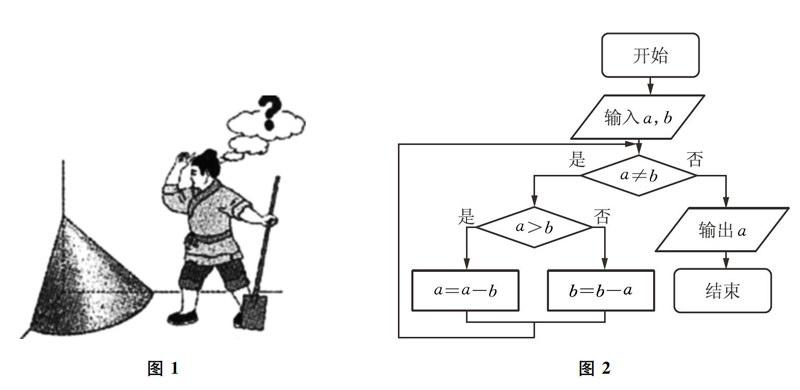
试题2 (2015年课标Ⅱ卷第8题)如图2所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为14,18,则输出的a=()
A.0
B.2
C.4
D. 14
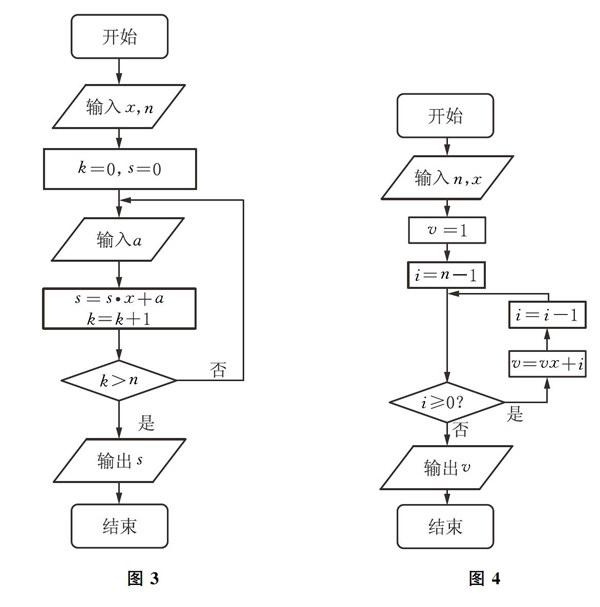
试题3 (2016年课标Ⅱ卷第8题)中国古代有计算多项式值的秦九韶算法,图3是实现该算法的程序框图.执行该程序框图,若输入的x=2.n=2,依次输入的a为2,2,5,则输出的s=()
A.7
B.12
C.1,
D. 34
两道题均取材于中国古代数学著名算法——更相减损术和秦九韶算法,而且都直接改编自教材——人教A版第一章《算法初步》第1.3节《算法案例》.2016年四川卷第6题也是考查秦九韶算法.
试题4 (2016年四川卷第6题)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图4所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为3,2.则输出v的值为( )
A.9
B.18
C.20
D. 35
通过对以上四道数学文化试题的对比分析,我们发现了解有关数学文化背景,可以领略古代算法思想的力量,理解問题及其算法的意义,摆脱机械解题训练造成的无意义学习与思想麻木,
三、关于备考数学文化试题的一点建议
以《九章算术》为代表的中国古代数学具有“寓理于算”的特征,这不同于以《几何原本》为代表的古希腊数学(他们注重逻辑的演绎).我国古代数学成绩辉煌,数学古籍有《周髀算经》《九章算术》等“算经十书”;宋元时期涌现出一批著名的数学家,如贾宪、秦九韶、杨辉、朱世杰等等,他们的数学成就在很多领域都达到了中国古代数学、甚至是当时世界数学的巅峰.
鉴于中国古代数学的特征,数学文化高考试题多集中在考查几何体、数列和算法等知识模块,如把古籍中的几何体(阳马、鳖膈、牟合方盖等)或古代器皿、测量工具(樽、天池盆)与三视图相结合,与数列相结合的古代名题(《九章算术》中此类问题较多,如竹九节等;2017年课标Ⅱ《算法统宗》“巍巍塔七层”等),更多的则是把著名的算法以框图形式考查,既回避古语原文,变晦涩为明了,抽象为直观,完全符合高考试卷的要求.
因此,以数学史、数学名著为背景的数学文化考题大多属于中档试题,要注重阅读理解试题的文字叙述与数学内涵,而不要被其外衣吓倒,可以发现试题考查的都是数学史上重要的或常规的知识、方法和思想.而这些,正是数学文化的要义所在.

