递推数列通项公式的求法

◎雷自学

数列知识是高中数学的必修内容，在高中数学中具有相当重要的地位。等差、等比数列知识及其应用是每年高考及各地模拟题中常出现的题型，尤其递推数列问题，更是学生数列基础知识掌握的程度与灵活应变能力的体现。怎样灵活快速准确的求递推数列的通项公式，笔者在此赘述几点，以飨读者。

一、叠加法

对于形如an+1＝an+f（n）的递推式，当f（n）为常数时，为一般等差数列，当 f（n）不为常数时，可先变形成 an+1-an＝f（n）的形式，然后逐项叠加，即可求得通项公式an．

例1．（2010年新课标全国卷·17题·12分）在数列｛an｝中，a1＝2，an+1＝an+3·22n-1，求通项an．

解：∵an+1＝an+3·22n-1∴an+1-an＝3·22n-1

∴an-an-1＝3·22n-3，an-1-an-2＝3·22n-5，an-2-an-3＝3·22n-7，

…，a3-a2＝3·23，a2-a1＝3·21．

把上面（n-1）个式子等号两边分别相加得：

二、叠乘法

对于形如 an+1＝an·f（n）的递推式，当 f（n）为非零常数时，为等比数列，当f（n）不为常数时，可先变形成的形式，然后再逐项相乘，即可求得通项公式an．

例2．已知数列｛an｝中，a1＝1，an+1＝an·2n，求an．

上面（n-1）个式子等号两边分别相乘得：

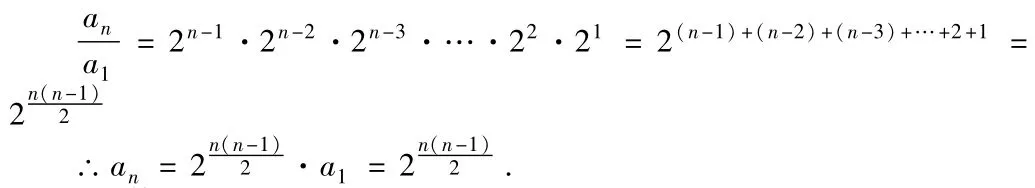
三、构造法

在数列 ｛an｝中，对于形如 an＝k·an-1+b（k、b为常数，k≠0）的递推式，当b≠0，k＝1时为一般等差数列；当b＝0时为一般等比数列；当k≠1且b≠0时，可将其变形成，于是可构造一等比数列．这是以为首项，公比为k的等比数列，则an可求。

例3．已知数列｛an｝中，a1＝1，an+1＝2an+3，求an．

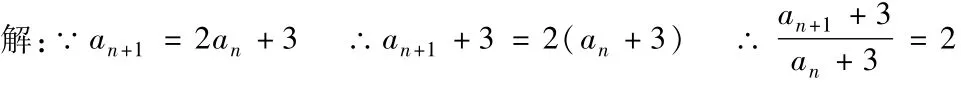
则数列｛an+3｝是以a1+3＝4为首项，公比为2的等比数列

∴an+3＝4·2n-1＝2n+1∴an＝2n+1-3．

四、数学归纳法

对于有些数列，可从已给出的首项入手，利用递推关系式，从特殊到一般，猜想确定通项公式，然后再用数学归纳法加以证明即可。这种解答数列问题的方法，也是历年高考命题的热点所在。

例4．在数列｛an｝中，，求 a2、a3、a4和 an．

（1）当 n＝1，2，3，4时，显然成立。

即当n＝k+1时，结论也成立。

综上，由（1）、（2）得，对一切n∈N*，都成立。

故，原数列｛an｝的通项公式就是

五、待定系数法

对于形如an+1＝Aan+B·Cn（A、B、C为常数）的递推式，可先引入待定系数λ，将递推式化为an+1+λ·Cn+1＝A（an+λ·Cn）的形式，然后再把它与原递推式进行比较，即可确定系数．这样得一数列｛an+λ·Cn｝就是以a1+λC为首项，公比为A的等比数列，则原数列｛an｝的通项公式可定。

例5．在数列｛an｝中，a1＝2，an+1＝4an+2·3n，求an．

解：设原递推式可化为an+1+λ·3n+1＝4（an+λ·3n）

即：an+1＝4an+λ·3n．与原递推式比较可得λ＝2

则数列｛an+2·3n｝是以a1+2×31＝8为首项，公比为4的等比数列。

∴an+2·3n＝8·4n-1＝2·4n

∴an＝2·4n-2·3n＝2·（4n-3n）．

六、换元法

在数列｛an｝中，对于形如（A、B为常数）的递推式，可先变形成，然后设，换元得，bn+1＝B·bn+A．这个形式和前面方法3中的递推式形式相同，因此可用构造法或待定系数法求出其通项bn，最后再换元即可得数列｛an｝的通项公式an．

例6．在数列｛an｝中，a1＝1，，求 an．

则数列｛bn+3｝是以为首项，公比为2的等比数列。

∴bn+3＝4·2n-1＝2n+1∴bn＝2n+1-3，再换元得：an＝．以上所述的各种方法是求递推数列通项公式的最常用方法，所列各种形式的递推式也是最常见的形式，其他好多形式的递推式通过变形大都可以变成上述各种形式中的某一种。当然还有一些不常见形式的递推式，对这些问题的解决笔者在此就不赘述了，留待有兴趣的同仁们作更进一步的探究挖掘，以便大家相互学习，共同提高。