需求受随机因素影响下零售商的最优订货策略
卢月莉,赵恒明,覃荣存
(广西大学行健文理学院, 南宁 530004)
延期支付是一种短期的商业信贷方式,也称为信用支付,已被广泛应用于商业贸易活动中。许多企业为了加速资金周转、及时收回货款、减少坏账损失,在提供信用支付策略的同时,往往采取一些优惠措施。若零售商承诺在更短的时间内付款,则供应商对货款给予一定的现金折扣,这不仅对零售商的购买数量及付款时间具有积极的影响,还可以促进双方建立起长期的合作关系。
文献[1]首先提出了允许延期支付的经济订购批量模型,随后许多文献从多方面对该模型进行了扩展。文献[2]在延期支付和价格折扣策略下,从供应商的角度研究有条件的延期支付策略设置问题。文献[3]基于两级信用支付研究了一个由单供应商和多个零售商组成的易腐品供应链的联合采购博弈问题。文献[4]基于两层次和等级信用支付策略研究了变质性产品的库存模型。文献[5]在考虑零售商风险偏好的情况下,研究了商业信用合同与收益共享契约组合下的供应链协调问题。一些文献在信用支付基础上结合现金折扣策略进行了拓展[6-12]。例如:文献[6]考虑了零售商采购价格与销售价格的差异;文献[7]对一般产品考虑了非瞬时补货的情形;文献[8]对变质产品考虑非瞬时补货的情况; 文献[9] 研究了几类确定性需求的产品的库存问题;文献[10]考虑了变质产品且需求依赖库存的情形;文献[11]研究了易腐产品的供应链一体化库存模型; 文献[12]在两货栈情形下研究了变质产品的最优订货策略。上述文献都是在产品需求为确定性的基础上进行的研究。
传统的库存问题研究通常把产品的需求作为外因,假设需求率为常数。然而,现实中许多产品的需求率并非固定不变,产品的市场需求可能会受到时间[13-16]、价格[17-18]、库存水平[19-20]等因素的影响。因此,研究需求受随机因素影响,供应商给予信用支付和现金折扣政策下的零售商最优订货策略更具有现实意义。本文在文献[9]的基础上,修正有关的研究假设,建立了供应商提供信用支付与现金折扣及考虑产品需求受随机因素影响下的零售商库存决策模型,并给出零售商在上述情况下的最优订购量和最优付款时间的计算方法。
1 假设与符号
本文所研究的供应链系统由一个零售商和一个供应商所构成,零售商在供应商给予的延期支付和现金折扣策略下决定最优的订购策略。为了便于建立模型,本文给出如下假设:
1) 库存系统只考虑单一产品,允许缺货。
2) 累积需求函数D(t)=α(t)+X,其中α(t)是关于时间t的函数且初始时刻α(0)=0;X是概率密度函数和分布函数分别为f(X)和F(X)的随机变量,且其数学期望E[X]=0。
3) 由于需求的不确定性,将采用经典报童问题的方法处理周期末可能会出现的产品剩余或缺货情况,即剩余产品将折价处理,而缺货会引起缺货惩罚。
4) 供应商给予不同的信用支付和现金折扣策略供零售商选择,零售商在信用期内无需支付任何货款,可利用累积的销售收入获得利息收益,而信用期结束时,零售商要立即向供应商支付所有货款,其未售出产品会因占用资金而产生利息支出。
模型所用的符号:Q为一个周期的订购量;T为订购周期;M为供应商给予零售商的延期支付期限;c为单位产品订购成本;p为单位产品销售价格;b为单位产品缺货费;g(g 本文考虑文献[9] 给出的订购策略: (1) 其中:cr是单位产品的最高订购价;Mi和δi一般由供应商根据历史经验制定。当M>M3时,c→∞,即供应商不提供过长的信用期,避免带来不可预见的风险。 基于上述分析与假设,零售商的利润=销售收入+残值+利息收益-订购费-缺货费-利息支付,各项计算如下: ① 订购费=cQ; ② 销售收入=pmin{Q,D(T)}; ③ 残值=g[Q-D(T)]+; ④ 缺货费=b[D(T)-Q]+; ⑤ 利息支付与利息收益和M与T的大小有关,分以下两种情形讨论: 情形1M TP1(Q)=pmin{Q,D(T)}-cQ+ g[Q-D(T)]+-b[D(T)-Q]++ 情形2M≥T 为了得到零售商的期望利润函数,首先根据需求函数D(t)=α(t)+X算出如下数学期望: 因此,当M 当M≥T时,零售商的期望利润为 其中i=1,2,3,M∈{M1,M2,M3}。 库存系统的目标是决策最优的订购量Q*使期望利润函数EP(Q)取得最大值,其中 为了方便讨论,令θ1=p-c+b+pIeM,θ2=p-g+b+pIeM+cIp(T-M),θ3=p-g+b+pIeM。 情形1M 分别求EP1i(Q)的1阶和2阶导数,得: (p-g+b)F(Q-α(T))- 证明由于α(t)是增函数且t≤T,则α(t)≤α(T),而分布函数F(X)也是增函数,则 情形2M≥T 同理,分别求EP2i(Q)的1阶和2阶导数,得: (p-g+b)F(Q-α(T))- (M-T)F(Q-α(T))] 证明由于α(t)是增函数且t≤T,则α(t)≤α(T),而分布函数F(X)也是增函数,则 现在讨论零售商的最优订购策略,即求解模型的算法: 步骤0 输入相应各参数。 下面将通过数值例子和灵敏度分析的方法介绍最优订购策略的求解过程,并分析不同参数变化对最优订购策略的影响。 例1 不同信用支付与现金折扣策略下的最优解。 当供应商分别提供两种不同的信用支付与现金折扣策略,而其他参数不变时,各种情形下的最优解如表1所示,比较得到零售商的最优订购方案分别为{EP11=4 769.78,Q*=142.71,M*=60/360}和{EP12=4 679.70,Q*=141.74,M*=120/360}。结果表明:不同的订购策略对期望利润的影响较为显著。一般来说,当供应商提供的现金折扣较高时,零售商选择较短的信用期所获利润更大。 表1 不同信用支付与现金折扣策略下的最优解 例2 需求的随机因子对订购策略的影响。 假设δ1=15%,δ2=10%,δ3=0%,其他参数与例1相同。当随机变量分布在不同范围时,最佳付款时间点为M*=M2=120/360,最优订购量与最优期望利润如表2所示。 表2 X对Q*和EP(Q*)的影响 从表2可知:当随机变量分布区间变大时,最优订购量变大,而最优期望利润变小。这说明,当产品的需求受到随机因素影响较为显著时,为了避免缺货带来如服务水平降低、缺货损失销售机会等不良影响,零售商需订购更多的产品来满足需求。而需求的不确定性会导致周期末出现产品剩余(折价处理)或缺货(产生缺货惩罚),因此期望利润会变小。由此可见:需求的不确定性对产品库存系统的影响不可忽视。 例3 缺货费和产品残值对订购策略的影响。 为了得到更显著的结果,假设X~U[-100,100],其他参数不变。计算得最佳付款时间点都是M*=M1=60/360年,而最优订购量与最优期望利润分别见表3、4。 表3 b对Q*和EP(Q*)的影响 表4 g对Q*和EP(Q*)的影响 从表3可以看出: 在随机变量的分布范围较大的情况下,当单位缺货费变大时,最优订购量和期望利润都只有微小变化,说明单位缺货费对最优订购量和期望利润的影响不大,零售商应该考虑订购更多的产品来满足需求,避免出现缺货,从而提高服务水平。 由表4可知:当单位商品残值变大时,最优订购量和期望利润都逐渐变大。这是因为当单位商品残值变大时,缺货对期望利润的影响较小,一方面,若需求变大则销售收入变大,从而利息收益变大;另一方面,若供过于求导致周期末产品有剩余,还有残值收入,此时零售商可以考虑订购更多的产品获得更大的利润。 供应商在给予零售商信用支付的同时,为了尽早收回货款,加速资金周转或减少坏账损失,往往会结合现金折扣来吸引零售商尽早支付货款。在现实生活中,产品的市场需求受到各种随机因素的影响,并非是固定不变的,具有一定的不确定性。因此,本文在考虑信用支付与现金折扣的基础上,考虑产品需求受随机因素影响的情形,建立了相应的零售商库存决策模型,使模型更接近实际情况,得到最优订购量和最优付款时间的计算方法,为零售商及时根据实际情况调整自己的订货策略提供了决策依据。2 模型的建立
















3 模型分析与求解
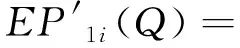





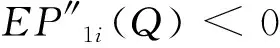
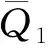
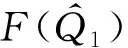
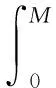
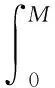

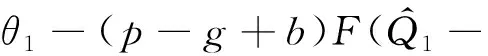


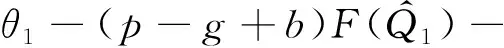
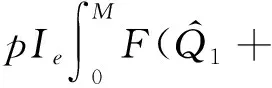















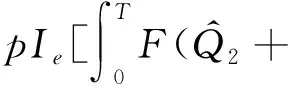
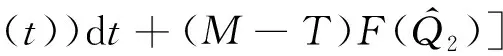
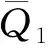

4 数值实例





5 结束语

