基于深度学习的极限工况下车辆的状态估计
张凤娇,汪 ,赵万忠
(1.常州机电职业技术学院, 江苏 常州 213164 ; 2.东南大学 机械工程学院, 南京 211189; 3.南京航空航天大学, 南京 210016)
车辆无人驾驶是目前研究的热点,提高其主动安全技术的关键问题之一是对车辆运动过程中的重要参数获取进行状态估计[1]。扩展卡尔曼滤波[2-3]、无迹卡尔曼滤波[4-5]、神经网络[6-7]、模糊逻辑[8]等算法都是对汽车控制系统中的关键控制变量(包括质心侧偏角、侧向速度、横摆角速度等)进行估计。但这些算法有其局限性,多数都是基于传统车辆动力学模型或者在假定算法参数固定的情况下来进行状态估计,模型的不精确和观测噪声的随机性可能会导致结果精度降低和滤波发散。
为了提高车辆状态估计算法的鲁棒性与估计精度,提出一种基于实验数据驱动建模的汽车状态估计算法。该算法利用前期实验数据基于长短时记忆网络(LSTM)训练生成具有时滞特性的非线性预测模型,输入一个可测参数向量,输出一个待估向量,可测参数向量和待估向量是一一对应关系。可测参数向量元素包括车速、纵横向加速度、前轮转角、路面附着系数,待估向量元素包括横摆角速度、质心侧偏角。
1 基于深度学习的状态估计框架
依据深度学习理论结合车辆关键状态精确估计需要提出一种基于深度学习的状态估计方法,框架如图1所示。
不同控制输入作用于实际的车,实际的车产生可测向量和待估向量的原始数据,利用LSTM搭建适当网络模型定义为初级人工车,此时网络未训练,将原始数据输入初级人工车经过训练产生具有较准确预测能力的高级人工车,此时高级人工车即为考虑时滞特性的非线性预测模型。车载传感器可以实时检测可测参数向量元素的具体值,将其输入到先前生成的高级人工车,自动输出车辆当前状态值,把状态输出给主动安全控制系统,主动安全控制系统给出实际控制输入,实际车接收控制输入又产生原始数据继续上一个循环过程,不断完成迭代更新,优化模型,提高估计精度。该极限工况估计框架使得模型具有在线学习和动态更新的能力。
模型驱动的估计方法一般基于纵向、侧向和横摆3个自由度的车辆模型进行状态估计。车辆动力学模型[9]如图2所示。
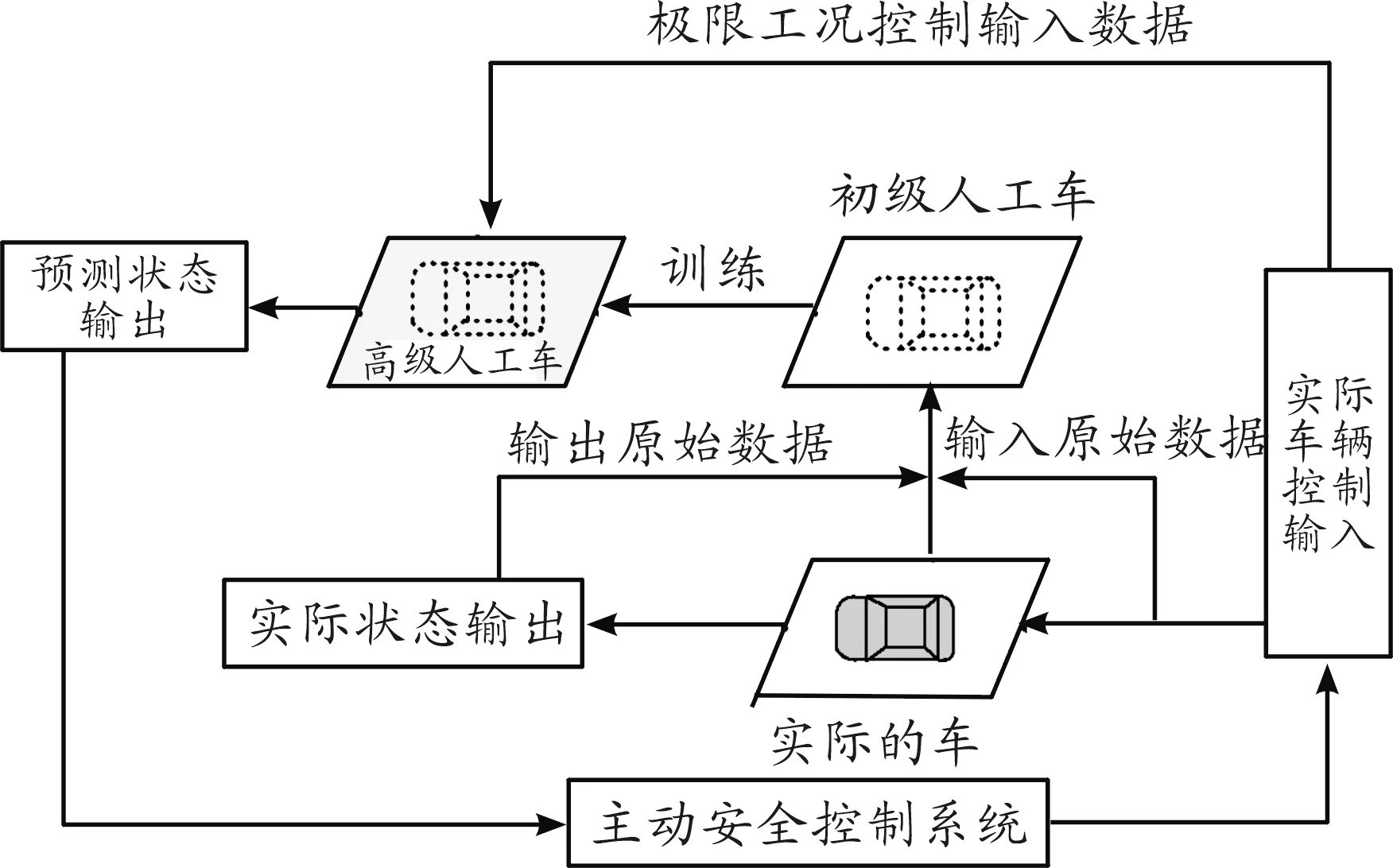
图1 极限工况状态估计框架

图2 3自由度车辆动力学模型
图2中,假设:车辆是对称的,XOY是固定在车辆质心处的坐标系,X轴在汽车的纵向对称轴上,规定X轴向前为正方向;Y轴在水平面内,与X轴垂直,通过车辆质心O点,规定向左为正方向。其中:方向盘转角等于前轮转角与方向盘转角到前轮转角的传动比的乘积。
对3自由度车辆模型建立方程:

(1)

(2)

(3)
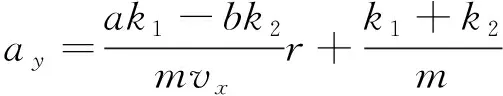
(4)
上述公式中参数含义见表1。
表1 变量命名与参数定义

参数名称变量参数名称变量纵向车速vx前轮侧偏刚度k1前轮转角δ后轮侧偏刚度k2纵向加速度ax路面附着系数μ侧向加速度ay前轴到质心的距离a横摆角速度r后轴到质心的距离b质心侧偏角β绕z轴的转动惯量Iz汽车总质量m
2 基于数据建模的网络设计
2.1 基于LSTM网络的搭建
车辆本身由于各种阻尼元件的存在,除了非线性特性外,车辆系统还是一个具有时滞特性的系统。当对车辆进行转向或者加减速等操纵时,车辆上一段时间内的状态对车辆下一时刻的状态存在一定影响,即在时间维度上,车辆在进行状态估计建模时应该考虑前上一段时间内系统状态量,但由于车辆系统本身的复杂特性这种时序上的影响很难用具体表达式去刻画,为此本文利用长短时记忆网络(LSTM)具有数据记忆的特性,构建多层LSTM网络模型来进行状态预测建模。
基于LSTM的车辆模型如图3所示。图3中输入的5个参数依次是车速、纵向加速度、横向加速度、路面附着系数、前轮转角;输出参数为质心侧偏角、横摆角速度。将实验数据样本输入到LSTM层进行状态预测,通过单层感知器将状态输出。在预测层,上一时刻LSTM预测模块的状态信息会作为输入进入下一时刻的LSTM预测模块,体现状态在时间上的连续性,可以较好地反映车辆系统的时滞特性。

图3 多层LSTM车辆模型
2.2 训练数据的采集
确定了深度神经网络的结构,影响模型输出结果关键就是训练数据的采集,采集的数据应满足如下原则:① 包括车辆线性和非线性状态;② 包括不同速度下车辆状态;③ 包括不同路面附着系数下车辆状态;④ 包括不同方向盘转角下车辆状态;⑤ 包括加速或减速下车辆状态。
传统的基于车辆动力学模型大都做了相应的简化,例如忽略悬架作用等,采用此方法进行状态估计必然会带来不可避免的误差。考虑到真实车辆模型的复杂性和非线性,本文采集实验数据的车辆模型来自成熟车辆动力学软件Carsim,选择的车型为D-Sedan,该模型包括动力总成、悬架、空气动力学、轮胎、ABS、转向系等非常复杂的模块,该模型比用传统方法建立的模型更加精确。为此,本文采集训练数据模型采用Carsim软件里车辆模型。在Carsim中设置仿真工况时间长度为10 s,采集训练数据工况如表2所示。

表2 采集数据不同的工况
在表2中:μ为路面附着系数;θmax为方向盘最大转角值。此处所述工况指由于路面、车速、制动压力、前轮转角4个参数变量变化引起车辆行驶状态发生改变的实验情况。不同路面下车速取3种典型值,方向盘转角变化范围如表2所示。为模拟车辆线性与非线性以及不同转角工况,本文采集数据时方向盘转角变化,如图4示:在1~2.5 s内转角为0;在2.5~7.5 s内转角做周期为2.5 s的正弦变化;在7.5~10 s内转角为0。不同的θmax的最大幅值不同。
给Carsim车辆模型输入图4方向盘转角变化值,仿真10 s结束后,在每种工况下可测参数向量元素和待估参数向量元素曲线上各取401个点记录到相应表格中,设置总的工况为13种,即输入可测向量和相应输出待估参数向量为4 812组数据用于网络训练。

图4 方向盘转角变化曲线
多层LSTM车辆模型基于Tensorflow平台搭建。多层LSTM车辆模型编译时优化器选择“Adamax”,损失函数选择“mse”。在进行训练时,通过改变网络层数、迭代次数、批处理大小等参数不断地进行调参,直到达到理想输出并保存该模型参数值。
3 基于虚拟实验的算法验证
在Carsim与Matlab/Simulink环境下建立联合仿真平台,如图5所示。EKF算法利用s-function函数实现,carsim模型输入是方向盘转角,输出的前轮转角、纵向和横向加速度作为EKF的输入,carsim输出的横摆角速度、质心侧偏角、纵向车速通过“From”和“Goto”模块与EKF输出做相应对比。选择普通前驱D级Sedan车型进行仿真,用于EKF算法的估计。整车的参数如表3所示。多层LSTM估计模型在深度学习框架keras下搭建并训练模型。多层LSTM为5层,每层输出数据分别为7维、16维、12维、10维和9维,最后一层为感知器,激活函数为“linear”。多层LSTM车辆模型的优化方法为Adam[10],损失函数为均方误差(MSE)。
(5)
其中:ot表示观察值;pt表示预测值。
扩展卡尔曼滤波算法(EKF)的过程噪声方差矩阵Q=diag[0.01,0.01,0.01],观测协方差设为定值R=[100];采样时间间隔为0.001 s。为验证EKF与深度网络搭建的人工车估计效果,随机选定高附着和低附着系数路面的2种工况来检验,工况设置如表4所示。

图5 仿真平台
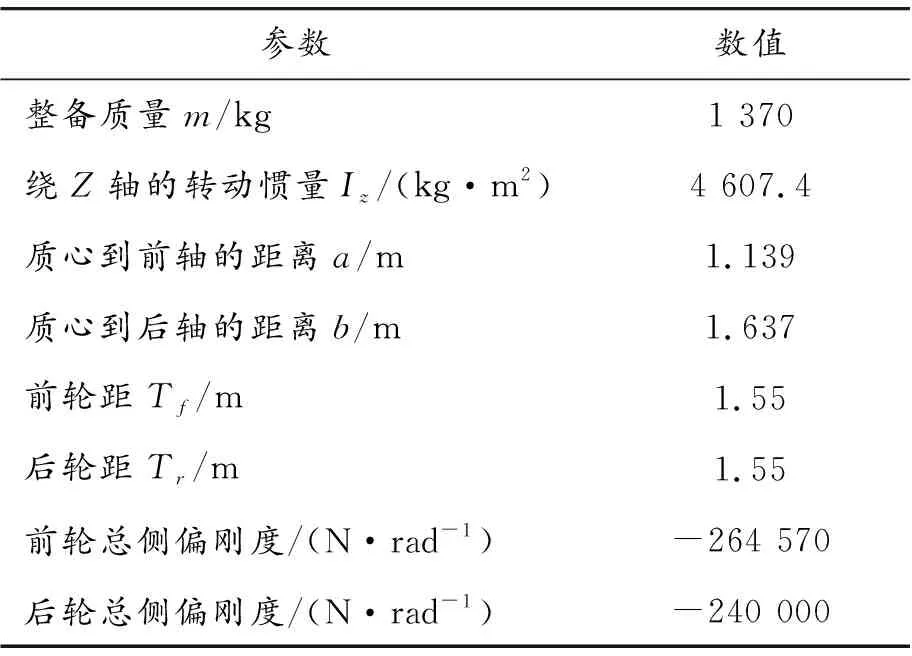
参数数值整备质量m/kg1 370绕Z轴的转动惯量Iz/(kg·m2)4 607.4质心到前轴的距离a/m1.139质心到后轴的距离b/m1.637前轮距Tf/m1.55后轮距Tr/m1.55前轮总侧偏刚度/(N·rad-1)-264 570后轮总侧偏刚度/(N·rad-1)-240 000

表4 验证工况
不同附着系数下EKF算法与多层LSTM模型的横摆角速度和横摆角速度绝对误差曲线如图6~9所示。

图6 高附着路面横摆角速度
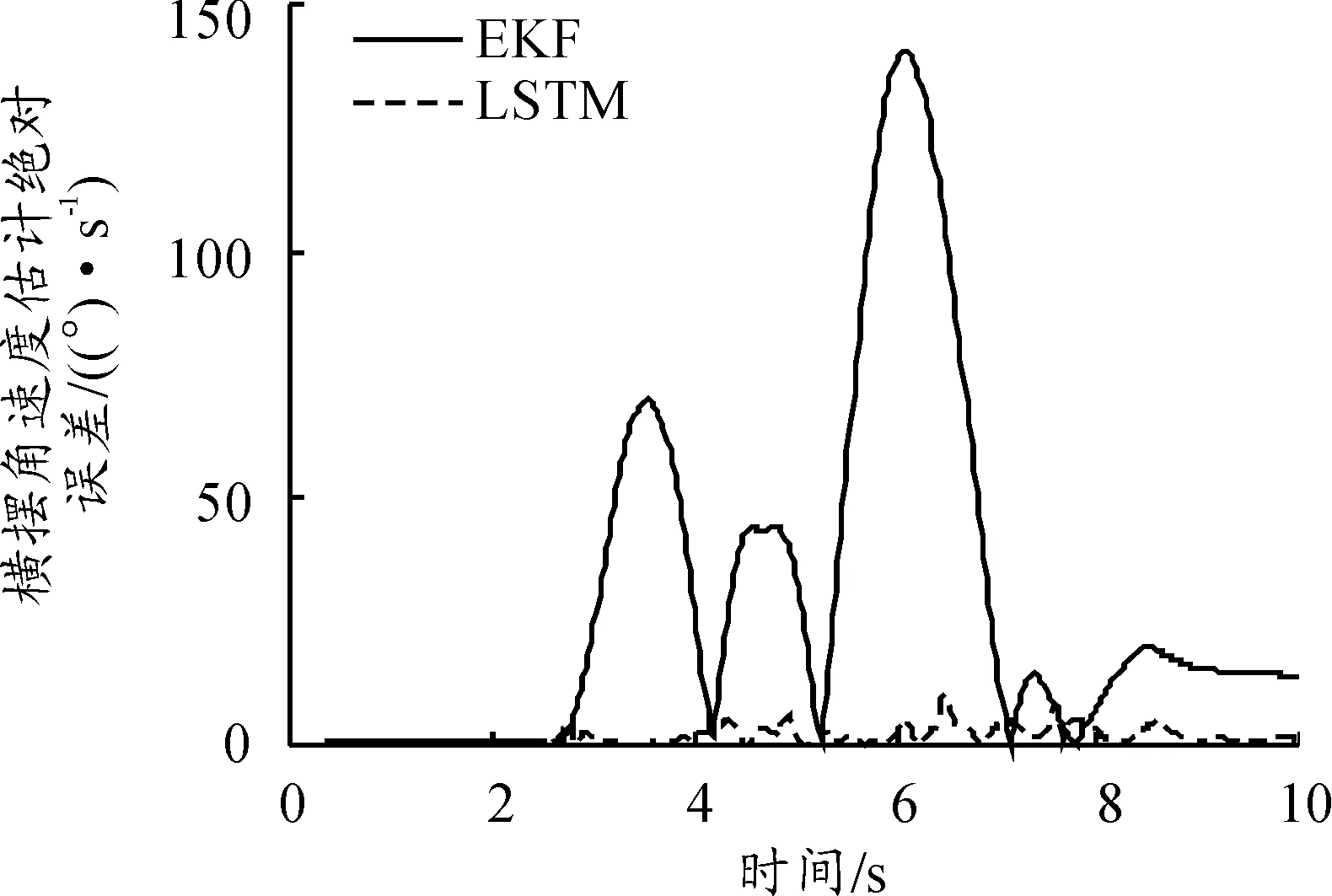
图7 高附着路面横摆角速度绝对误差
在如图6所示的高附着路面工况时, LSTM算法估计值贴近真实值,EKF算法估计值与真实值偏差较大。通过图7绝对误差曲线可知:EKF算法估计瞬态偏差最大,LSTM算法估计瞬态偏差较小。

图8 低附着路面横摆角速度

图9 低附着路面横摆角速度绝对误差
在如图8所示的低附着路面工况时,LSTM算法估计值贴近真实值,EKF算法估计值与真实值偏差较大。通过图9其绝对误差曲线可知:EKF算法估计瞬态偏差最大, LSTM算法估计瞬态偏差较小。通过上述不同路面下横摆角速度估计对比曲线可知,LSTM估计算法精度优于扩展卡尔曼滤波算法。EKF算法估计曲线出现较大偏差,原因在于假定观测噪声和过程噪声不变,前后轮侧偏刚度不变,在不同路面不同转角不同速度下上述参数均发生了变化,且EKF估计算法车辆动力学模型忽略了悬架的作用,在车辆有较大横摆角速度时,载荷转移是不能忽略的重要影响因素,基于上述原因EKF估计必然导致巨大偏差。为了进一步定量地比较2种算法的估计精度,给出了估计值相对于实际值的均方根误差(RSME)和标准误差(SE),如表5和表6所示。在表5和表6中可以看到:在不同附着路面下,EKF的两种性能指标远远劣于LSTM估计算法,LSTM算法性能指标在两种算法中最优,不但距离真实值偏差较小而且误差波动范围也较小。
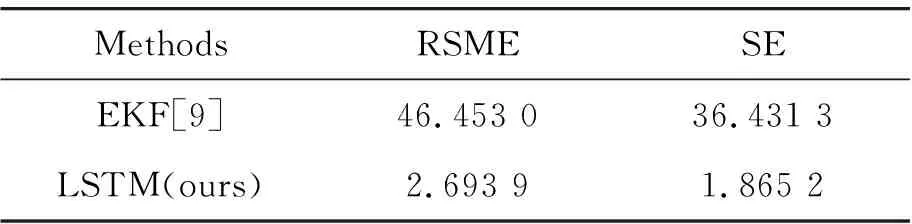
表5 高附着路面横摆角速度估计误差

表6 低附着路面横摆角速度估计误差
不同附着系数下EKF算法与多层LSTM模型质心侧偏角和质心侧偏角速度绝对误差曲线如图10~13所示。

图10 高附着路面质心侧偏角
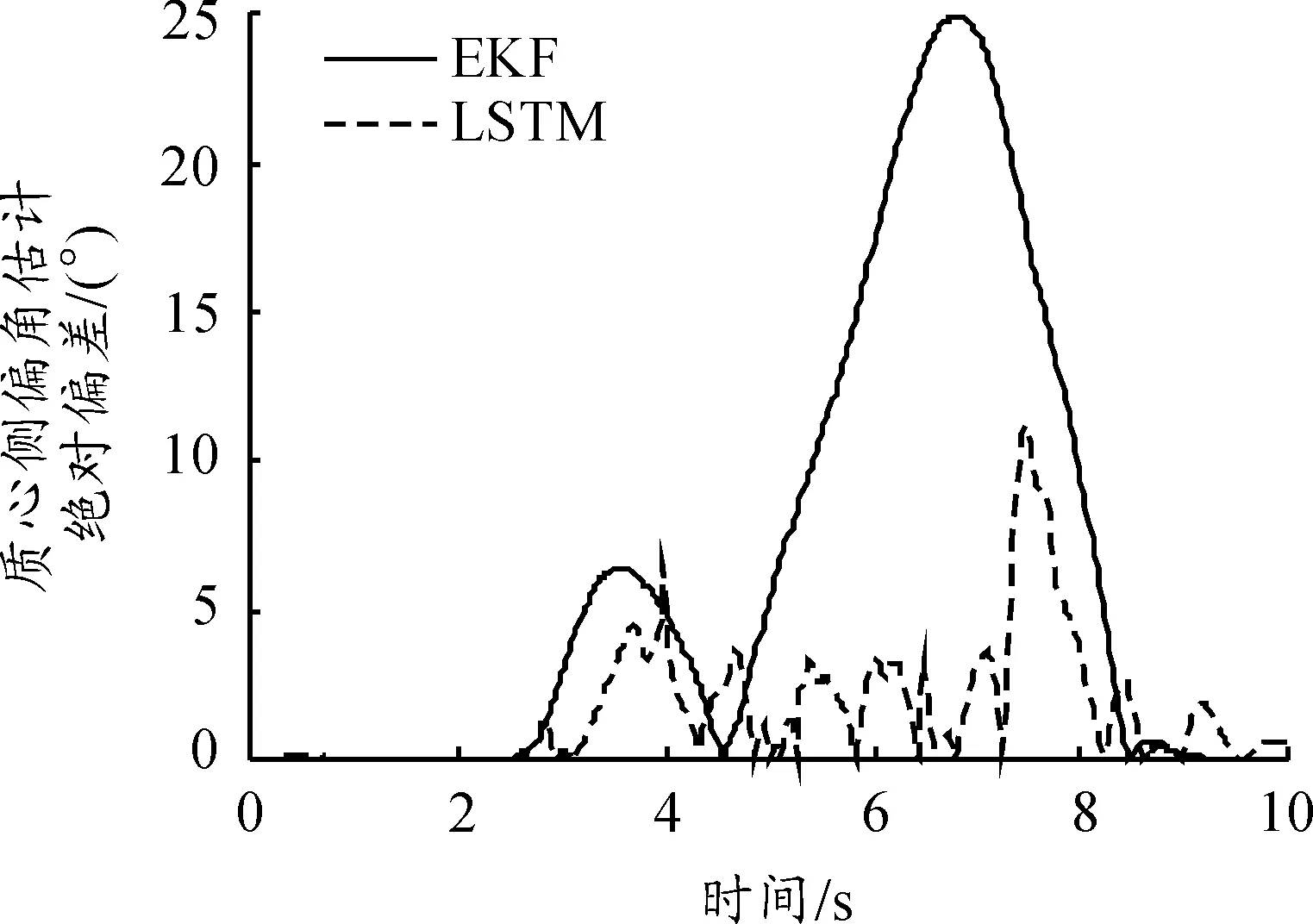
图11 高附着路面质心侧偏角绝对偏差
在如图10所示的高附着路面时,质心侧偏角LSTM算法估计值贴近真实值,EKF算法估计值与真实值偏差较大。通过图11其绝对误差曲线可知:EKF算法估计瞬态偏差最大,LSTM算法估计瞬态偏差较小。

图12 低附着路面质心侧偏角

图13 低附着路面质心侧偏角绝对误差
在如图12所示的低附着路面工况时,LSTM算法估计值贴近真实值,EKF算法估计值与真实值偏差较大。通过图13其绝对误差曲线可知:EKF算法估计瞬态偏差最大, LSTM算法估计瞬态偏差较小。通过上述不同工况下横摆角速度估计对比曲线可知,LSTM估计算法精度优于扩展卡尔曼滤波算法。2种不同路面下质心侧偏角EKF估计值偏差较大原因同横摆角速度偏差原因。同时我们看到,不同附着路面下横摆角速度和质心侧偏角的LSTM曲线估计值都在真实值附近波动,没有出现较大偏离,说明基于数据驱动的建模方法得出的非线性预测模型能很好地表征车辆处于极限工况下的非线性动力学响应而EKF算法不具备此能力。
为了进一步定量地比较2种算法的估计精度,给出了估计值相对于实际值的均方根误差(RSME)和标准误差(SE),如表7和表8所示。在表7和表8中可以看到:在不同附着路面下,EKF的2种性能指标远远劣于LSTM估计算法,LSTM算法性能指标在2种算法中最优。不但距离真实值偏差较小而且误差波动范围也较小。

表7 高附着路面质心侧偏角估计误差
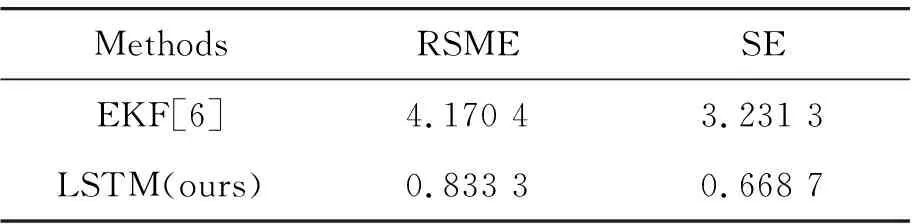
表8 低附着路面质心侧偏角估计误差
综合图5~13和表5~8可知:依据实验数据,利用LSTM网络具有短期记忆特性生成具有时滞特性的非线性模型。改变传统估计算法依赖模型的精度的缺陷,利用数据驱动提高了估计精度。虚拟实验验证表明,LSTM算法估计结果优于单纯的EKF算法,具有较好的精度和鲁棒性。
4 结束语
提出一种基于实验数据驱动建模的汽车极限工况下状态估计算法。依据实验数据,利用LSTM网络具有短期记忆特性生成具有时滞特性的非线性模型。改变传统估计算法依赖模型的精度的缺陷,利用数据驱动提高了估计精度。
虚拟实验验证表明,LSTM算法估计结果优于单纯的EKF算法,具有较好的精度和鲁棒性。
对于基于数据驱动的估计模型尚未考虑坡道和变附着系数路面工况,需要后续进一步完善;对于状态估计的大数据本文实验数据相对较少,需要后续大量计算实验产生大数据,尽可能覆盖整个状态估计的解空间。

