基于多谐波源同次谐波叠加模型的仿真研究

曹 栋，扈罗全，2，俞建峰

(1.苏州大学 轨道交通学院， 江苏 苏州 215021； 2.苏州出入境检验检疫局， 江苏 苏州 215104； 3.江南大学 机械工程学院， 江苏 无锡 214122)

随着电力电子技术的飞速发展，各类电力电子装置在电力系统、工业、交通及家庭中的应用越来越广泛，也使得谐波造成的危害日趋严重[1]。针对谐波源叠加问题国内外研究人员主要采用实测法和解析法对铁路谐波进行分析研究。实测法是通过对牵引网某处的谐波进行测量，运用统计的方法得到该处谐波电流的统计特性，但需要大量的实测数据；解析法是采用概率学理论，求多个随机谐波电流之和的概率密度函数，尚局限于卷积法，即假定随机变量之间相互独立[2]。目前，施行的国家标准GB/T 14549—93[3]和IEC标准IEC TR 61000-3-6：2008[4]基于工程经验和实测数据，给出了谐波叠加的加权因子。

当前学术界对这两种标准仍存在争议，主要是因为加权因子的确定是在一定的分布假设下得到的，而不同谐波源具有不同的分布特性，因此标准模型的计算精度是有限的[5]。大量现场测试表明：谐波源所产生的谐波电流随时间变化呈非平稳的随机过程，且在同一个网络中各谐波源所产生的谐波电流具有相关性。多个谐波源同时作用于电网时，可能存在相互抵消因素，这又恰恰是最难详尽分析的。如果按照国标推荐公式来计算多谐波源网络谐波电流和谐波电压，其计算结果往往偏离实际值，从而造成计算结果偏大[6]。

文献[7]结合功率因数的定义和物理意义，把PCC端和分谐波源端的功率因数作为加权因子，构建新的叠加模型。本文针对国家标准、IEC标准和新的公式，利用仿真软件搭建多谐波源模型，通过误差分析比较3种公式的计算精度。

1 叠加模型

1.1 国家标准与IEC标准

由国家标准GB/T 14549—93[3]，两个谐波源的同次谐波在同一条线路的同一相上迭加，当相位角不确定时，可按式(1)进行如下计算：

(1)

式中，Ih1为谐波源1的第h次谐波电流(A);Ih2为谐波源2的第h次谐波电流(A)；Kh系数按表1取值。

表1 kh系数推荐

由国际电工委员会(IEC)标准IEC TR 61000-3-6：2008[4]给出了对所考虑的一组谐波源(取95%的概率统计值)进行数学运算通用的求和方法，可以表示成：

(2)

α的取值如表2所示。

表2 α取值推荐

以上两种标准均是通过工程经验确定叠加系数。

1.2 基于基波的功率因子叠加模型

1.2.1 功率因数计算方法

在非正弦电路中，参考文献[8]关于功率因数的计算方法，按照如下公式计算：

(3)

其中Uk、Ik分别为第k次谐波电压、谐波电流的有效值。假设输入侧无损耗，相当于电源电压不失真，则式(3)中Uk=0(k≥2)，可将式(3)化简为：

(4)

1.2.2 基于功率因数加权的叠加公式

包含了功率因数的加权谐波分量线性叠加方法可用来描述相关谐波分量的贡献，即相当于将功率因数设置为权重因子[7]。

(5)

式中：F为公共节点的功率因数;fj为分谐波源的功率因数;h为谐波次数；j为第j个谐波源。

此处的功率因数F针对非正弦电路，所以F是综合考虑基波和各次谐波的权重因子，需按照式(4)进行计算。

2 多谐波源模型搭建

2.1 谐波源模块

通过仿真软件中的simulink模块，搭建一个简单的多谐波源系统。在电力电子器件中，整流电路将交流电变为直流电输出，在家用电器中应用较多的为桥式整流电路。本模型的谐波源主要来自单相全控桥式整流电路和阻抗负载，见图1。通过设置整流电路中的触发角以及阻抗负载，使得每个谐波源产生不同程度、不同波形的谐波电流。

本文共建立了3个谐波源，其中2个谐波源的畸变率设置在5%以内；为了突出谐波源叠加对于总谐波畸变率的影响，另一个谐波源设置为25.6%。

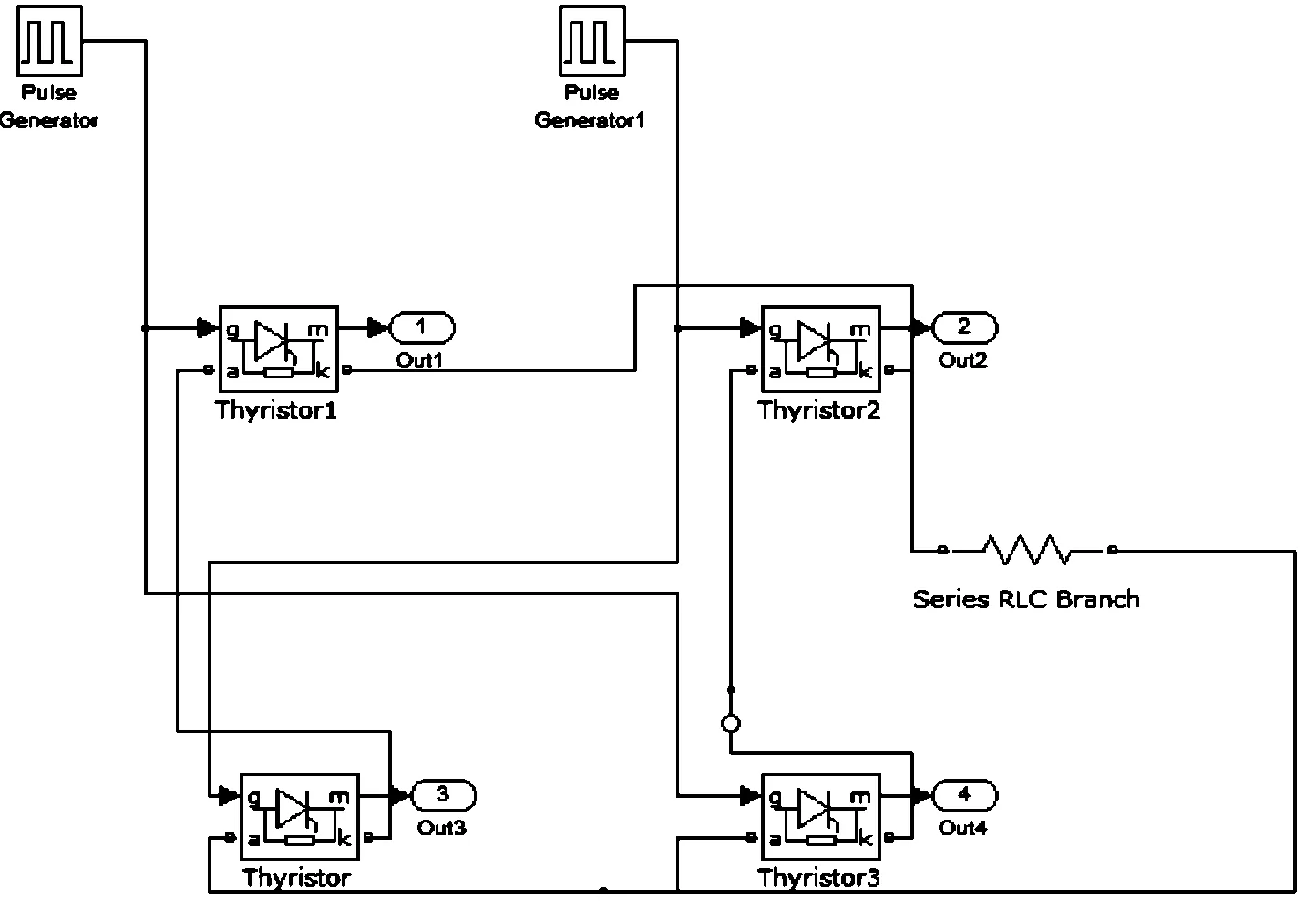
图1 全控桥式整流电路

2.2 功率因数测量

根据式(4)，非正弦电路功率因数与基波相位角θ、总谐波畸变率THD有关。文献[8]提出了在非正弦电路中测量功率因数的方法，这种方法同样适用于三相电路中功率因数的测量[10]。

3 仿真结果

3.1 单谐波源和谐波源叠加仿真数据

由于模型产生偶次谐波电流较小，在一些标准中也不予考虑，故本文忽略不计。多个谐波源叠加的数据见表3。

3.2 叠加计算

数据前文提到的国家标准、IEC标准，以及新型叠加模型3种公式计算结果见表4。

3.3 误差计算

通过公式：

误差=(计算值—测量值)/测量值×100%

(6)

计算误差，求出3种叠加公式得到的各次谐波与仿真电路得到的数据之间的误差，见表5。

由误差分析可得，采用新的叠加模型相较于其他2种公式，对于3、5次谐波的计算误差较小，对于7、9次高次谐波计算误差较大。这是由于高次谐波电流值较小，难以达到计算精度。

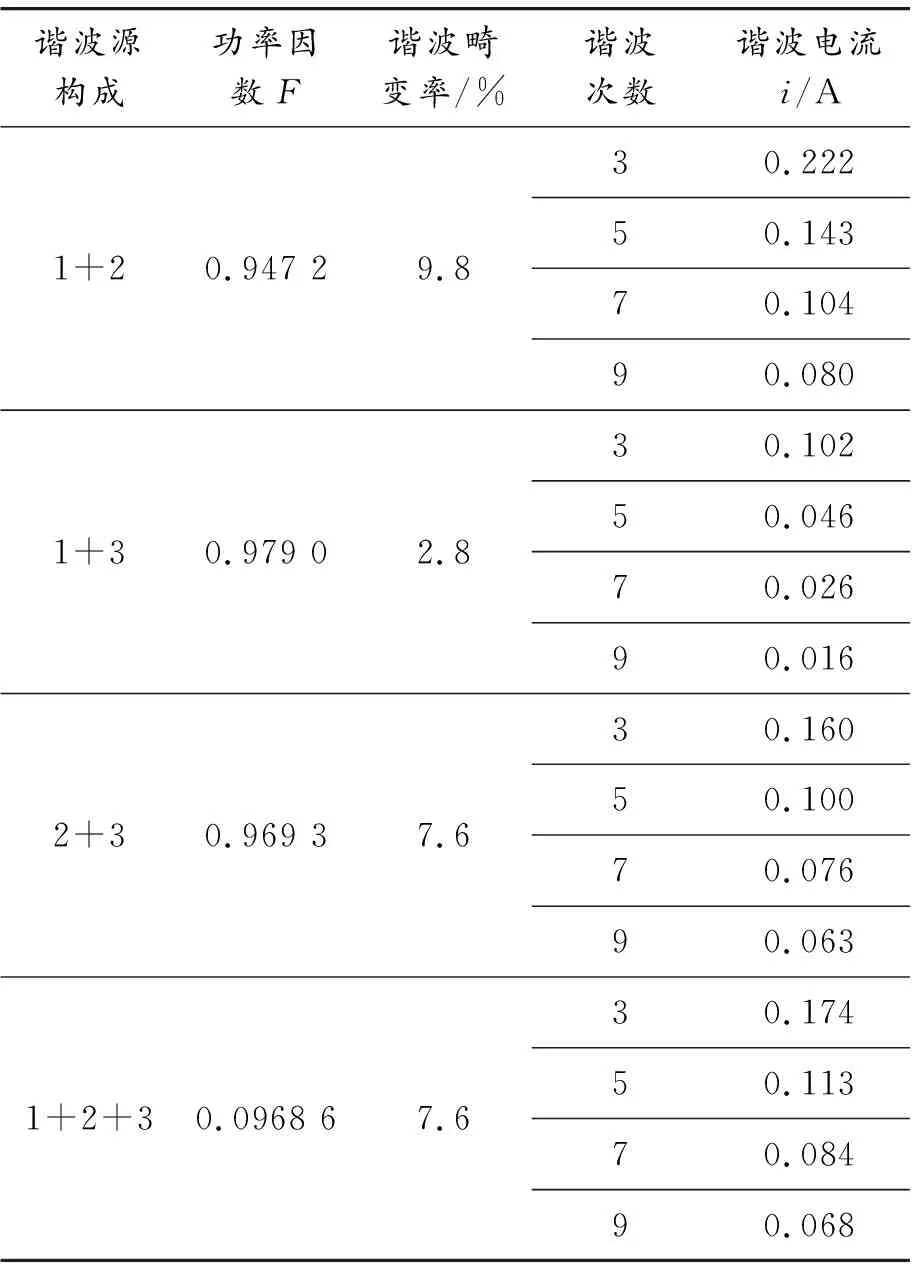
表3 多谐波源矢量和

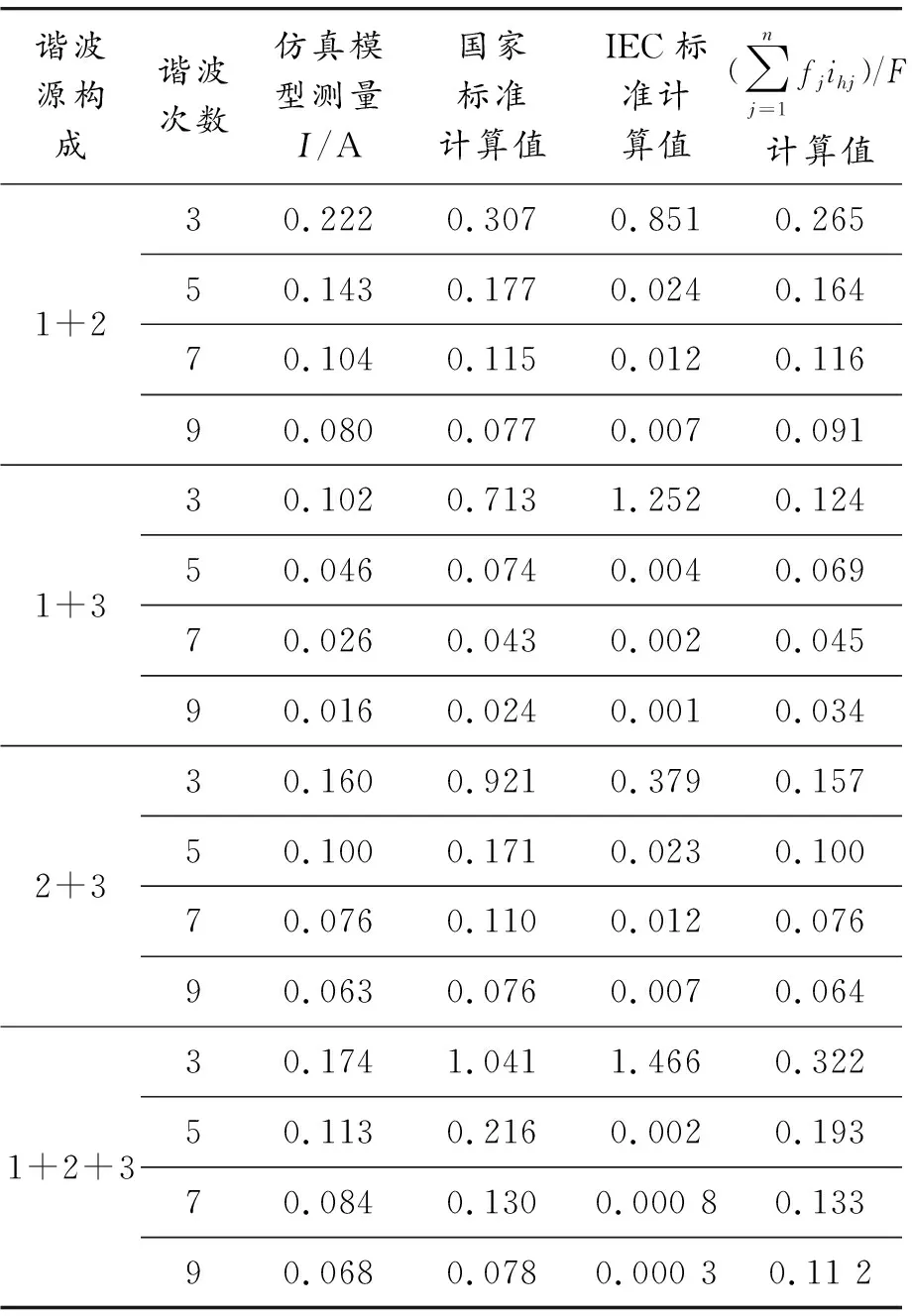
表4 叠加公式计算结果

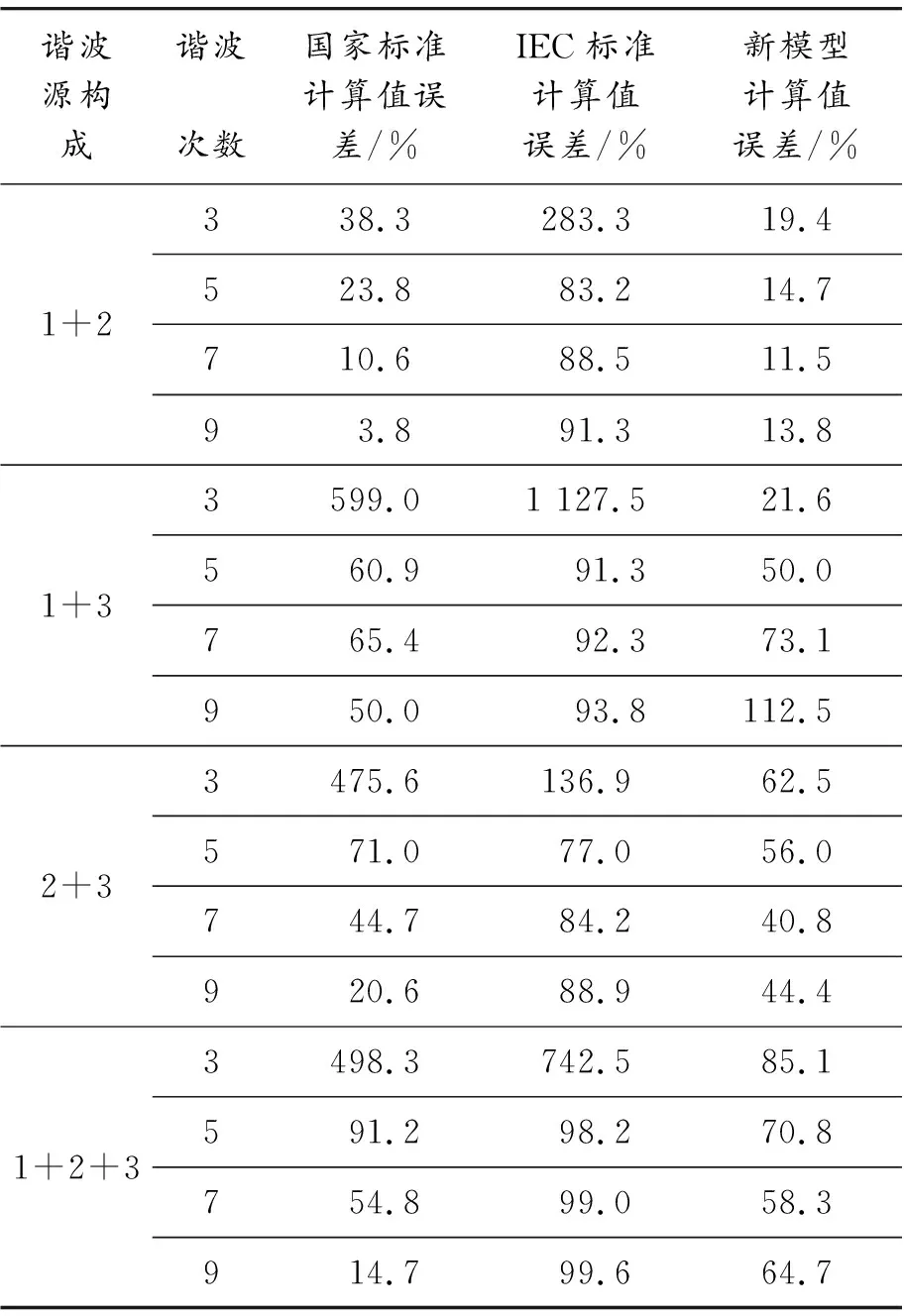
表5 误差分析

4 结束语

功率因数是衡量电气设备效率的一个系数。功率因数低表明电路用于交变磁场转换的无功功率大，相应产生的谐波畸变率增加。由公式(4)可以看出：谐波畸变率对电路实际功率因数影响很大。通常电器设备所标的功率因数是位移功率因数，是在理想正弦电流电压波形下测得的[10]。当电压或电流中有谐波存在时，实际的功率因数小于所标的功率因数。因此，以此公式算出的功率因数综合考虑到谐波的情况，把它作为权重因子是非常适用的。

通过搭建的多谐波源模型，并就3种公式进行误差分析。结果表明：相较两种标准中的计算精度，基于非正弦电路下功率因数计算模型的加权线性叠加方法效果更好。