应用Tsallis算法和关键度度量的决策树构建

李 梁，丛培强，陈亚茹

(重庆理工大学 计算机科学与工程学院， 重庆 400054)

决策树是机器学习的主要方法之一，在一些领域仍在积极研究，如图像插值、语音综合[1-5]。决策树是根树结构，容易理解，并且有较好的计算结果和计算效率，其中每个非叶节点是决策节点，其表示将情况分成两个或多个子树的标准，每个分支代表当前节点1种分类情况，每个叶节点表示整个数据集1种分类情况，自根节点至每个叶节点存在1条路径，代表1种分类途径。决策树分类器是自上而下的构建过程，并进行预剪枝和后剪枝，预剪枝是在完全正确分裂训练集之前，较早地停止树的生成，后剪枝是在完全生成树结构后进行剪枝。决策树分类器通过使用节点中的条件来决定分支，从根节点向下移动到叶节点，从而为任何看不见的情况预测类别。

当前有很多文章对决策树提出了改进，徐鹏等[6]提出C4.5-K，在C4.5中引入了可调节参数K，限制信息增益率的取值范围，取得较好的性能，但是该算法只面向期货数据有较好效果；李孝伟等[7]提出了基于分类规则选取的C4.5改进算法，但对复杂样本分类问题有待进一步研究；宋广陵等[8]提出了A-CART，能产生多个子节点，但是该算法只适用于两分类问题。

决策树的核心问题是树的构建过程，也就是属性的分割问题，在过去几十年出现了一系列文献，提出了一些分割算法，其中最具代表性的如ID3、C4.5、CART等。ID3基于香农熵构建决策树；C4.5基于信息增益率，被认为是归一化的香农熵，弥补了ID3不能处理连续属性的缺陷；而CART算法基于基尼系数。这些算法是独立存在的，都有各自相应的优势。本文提出了一个统一的Tsallis熵框架，这不仅统一了上述3种流行分割标准，而且还可以通过可调参数q值来适应各种数据集。

训练样本集存在样本分类不平衡的情况，也存在小类属数据集的问题，即在训练集中有些类属的样本数量远远小于其他样本数量，见表1。假设构建的决策树只有2个叶节点，A1和A2表示当前叶节点样本数据类别，即A1和A2样本数据各有 2 000个和200个，A2属于小类属；在决策树构建过程中，对叶节点进行类属标识时，采用“少数服从多数”的标准，即在对叶节点进行类属标识时，选出该节点样本数量最多的类，并以该类标识叶节点。对表1而言，叶节点1与叶节点2均被标识为A1，小类属A2被忽略。由于上述两点，使得小类属被忽略，在预测新数据时，无法判别出小类属数据。 为解决该问题，本文提出关键度度量，取代“少数服从多数”的标准。

表1 训练样本实例

1 Tsallis熵框架

1.1 Tsallis熵

为了解决非广延熵问题，Tsallis受多重分形的启示，提出了非广延熵的概念。 Tsallis熵定义如下：

，q∈R

(1)

其中：X取值为{X1，X2,…,Xn}；随机变量p(Xi)是Xi的概率。

1.2 Tsallis熵框架

香农熵、增益比率和基尼指数统一于Tsallis熵框架中，Tsallis熵与三者的具体对应关系如下：

1) 当可调参数q→1时，Tsallis熵等价为香农熵。

(2)

2) 当可调参数q→2时，Tsallis熵等价为基尼指数Gini。

(3)

计算信息增益率CainRatio(GR)时，将计算香农熵的过程替换为计算Tsallis熵的过程，则信息增益率就转变成了Tsallis信息增益率(TGR)。

当可调参数q→1时，TGR等价为基尼指数Gini。

(4)

调节不同的q，Tsallis熵退化为香农熵、信息增益率和基尼指数。因此，可以通过调节q的值来提高构建决策树的性能。

2 关键度度量

决策树叶节点的标识基于“少数服从多数”原则，在某些领域该原则能代表整体数据，但对分类问题，该原则忽略了一些少数但不可忽略的类别，或许这些类别才是更重要的。该问题出现的原因在于：对叶节点进行标识时只考虑到属于叶节点j的样本数据集，而并未考虑到总体样本数据集。在训练样本集中，一些类Ai的样本数量远远小于其他类别样本数量，并在构建决策树过程中该类别数据不断被划分到不同叶节点，最终在各样本子集中，Aj类别的样本数量占据较小比例。因此，使用关键度度量标准替代“少数服从多数”原则，不仅考虑当前叶节点中的各类样本数据比例，也注重各类样本总体数量，能完全解决小类属被忽略的问题。

定义1 类分散度aij表示类Ai在节点j的分散程度，即节点j中Aj类样本数量占总训练样本集中Ai的比例。

(5)

定义2 类决策度βij描述第i类样本在节点j的权威性，即节点j中Ai类样本数量占节点j中样本数据的比例。

(6)

当建立完决策树，对叶节点进行标识时时，综合考虑aij和βij，βij表示当前类i的样本在叶节点j中所占比例。未改进前，决策树构建以βij为基础按照“少数服从多数”的标准标识叶节点；改进后，不仅考虑βij，同时还将考虑aij，解决了小类属无“话语权”的缺陷。当βij>0.8时，以类i标识叶节点j；当βij≤0.8时，使用关键度度量作为标识标准。

定义3 关键度度量dij为类分散度和类决策度的乘积，即

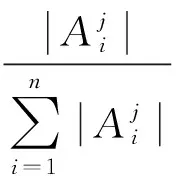
(7)

由式(6)(7)可知：aij和βij取值范围均为[0，1]，因此dij取值范围为[0，1]。当dij越接近1，则类i作为叶节点j的可能性越大；当dij=1时说明类i中所有样本数据均分布在叶节点j，并且节点j中的类属是纯类。提出关键度度量后，为叶节点进行类标识时，选取关键度度量最大的类别，而不是选择样本数据最多的类别。

由上述可知：最终叶节点的标识类选取标准为

select(Ai)=arg max{dij}

(8)

对于表1，其类分散度和类决策度如表2所示。

表2 分散度和决策度

叶节点1：d11=a11β11=0.894 6，d21=a21β21=0.000 3

叶节点2：d12=a12β12=0.051 3，d22=a22β22=0.462 7

改进前，对表1中叶节点的类别标识以“少数服从多数”为标准。叶节点1以A1为标识，叶节点2以A2为标识。在本训练样本数据集中，A2属于小类属，被忽略掉。改进后，以“关键度度量”为标准，叶节点1中β11>0.8，所以叶节点1的类标识为A1；叶节点1中β11<0.8，A2类的关键度度量较大，所以叶节点2的类标识为A2，解决了小类属属性被忽略的缺陷。

3 基于Tsallis熵框架和关键度度量的决策树构建

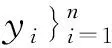
(9)

决策树构建完成后，需要标识每个叶节点的类别，此时摒弃原始“少数服从多数”的原则，采用关键度度量的方式标识每个叶节点属于哪种类别。遍历所有叶节点，根据式(7)计算出每个叶节点中不同类别对应的关键度度量，由式(8)得到当前叶节点标识为关键度度量最大的类别。至此，决策树构建完成。

4 实验

本实验分为两部分：第1部分是在不同数据集上使用Tsallis框架和ID3、C4.5、CART算法形成决策树，以这两种决策树为对测试样本集进行分类，比较分类结果的准确度和树规模，验证本文基于Tsallis框架构建决策树的性能；第2部分为在不同数据集上使用Tsallis框架构建决策树时，引入“关键度度量”准则进行叶节点的标识，并在测试集上验证准确度和决策树规模，并与第1部分基于Tsallis框架构建决策树进行比较。

4.1 基于Tsallis框架构建决策树性能分析

在不同数据集上基于Tsallis框架和ID3、C4.5、CART算法构建决策树并进行测试，比较准确度和决策树规模。实验数据采用UCI中Abalone数据集、Census Income数据集、Connect-4数据集、Image Segmentation 数据集、Mushroom数据集，决策树构建过程同本文第3节，每组数据样本包含的各类样本数量均相同，因此避免了数据集中小类属现象，得到5组测试结果，如表3所示。

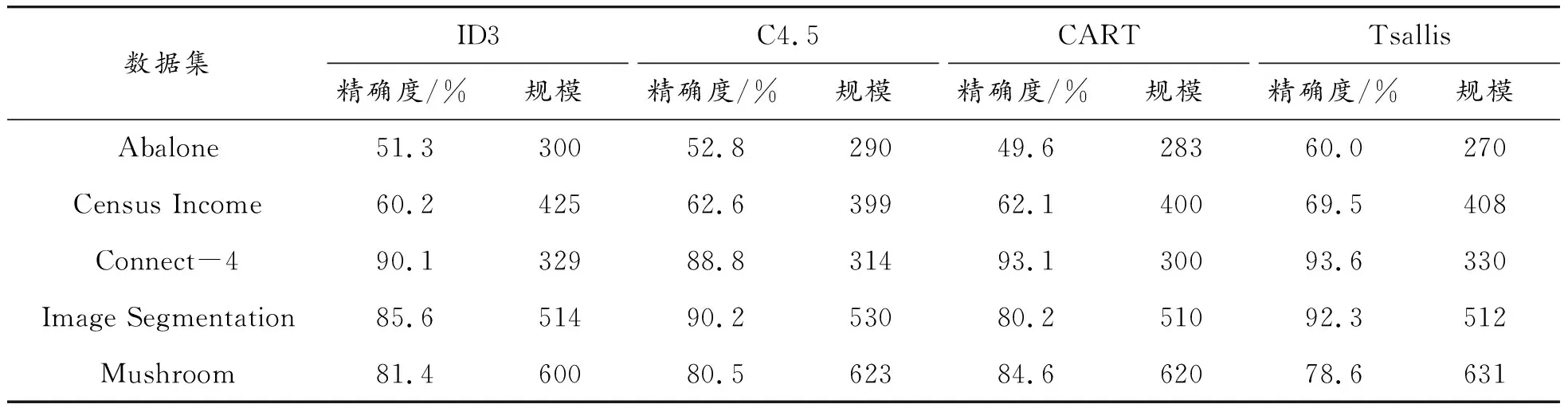
表3 基于Tsallis的决策树

在Abalone数据集、Census Income数据集和Image Segmentation数据集上，采用C4.5分割算法构建决策树准确度相对ID3和CART较好；在决策树规模上，CART在Abalone数据集、Connect-4数据集和Image Segmentation数据集上性能好于ID3和C4.5分割算法。但是，基于Tsallis框架构建的决策树，除Mushroom数据集外，准确度和树规模上均好于其他3种经典算法，尤其是Abalone数据集，性能提高更加明显。

4.2 基于Tsallis框架和关键度度量构建决策树性能分析

在基于Tsallis框架构建决策树的基础上，以本文提出的“关键度度量”为基准标识叶节点，并在测试集上测试。其中，验证部分仍采用10折交叉验证法，但数据集中每类样本数据不再均分到每组样本，而是将数据集随机分为10份，因此训练数据集和测试样本集中便会出现小类属缺陷，目的为验证本文提出的“关键度度量”标准，测试结果如表4所示。

表4 基于Tsallis框架和关键度度量的决策树

对比表3和表4可知：出现小类属属性后的数据集，以Tsallis算法构建决策树，准确性均有所下降，决策树规模一定程度增大。当数据集中出现小类属后，Tsallis仍以“少数服从多数”原则标识叶节点，因此小类属分类被忽略后，在测试阶段该类数据样本被分错类。当“关键度度量”取代“少数服从多数”标准后，在同样的数据集上进行测试，准确度提高了，决策树规模下降了，且相比本文1.2节基于Tsallis框架构建决策树的性能也提高了。

4.3 不同参数q对构建决策树的影响

本实验采用UCI中Abalone数据集，该数据集有4 177个样本实例，8个决策属性，一个类别属性，决策属性中有1个离散属性和7个连续属性。调节q参数，调节范围为[0.1，10.0]，q的变化梯度为0.1，对每个q验证决策树准确度和规模，将分类正确的样本数量占测试集样本数量的比重作为准确度。

实验采用10折交叉验证法，验证构建决策树的准确度和节点规模，整体Abalone数据集分为10组，每组数据集包含每类样本均分的1/10，将其中任意9组样本作为训练集，剩余1组作为测试集，得到10组测试结果，求得10组准确度的平均值作为最终的准确度。不同q值在Abalone数据集上测试结果如图1所示，图1(a)是准确度，图1(b)是决策树规模。图1(a)显示：精确度对于参数q变化是敏感的，最高精确度在q=2.4处取得。图1(b)显示：决策树规模对于参数q变化也是敏感的，最小决策树规模在q=3.9处取得。最终，高精确度和低规模可以在q=1.7的位置取得。该实验表明了参数q对决策树精度和规模存在影响，在实际应用中可以根据精度和规模的侧重点不同，调节q的取值。

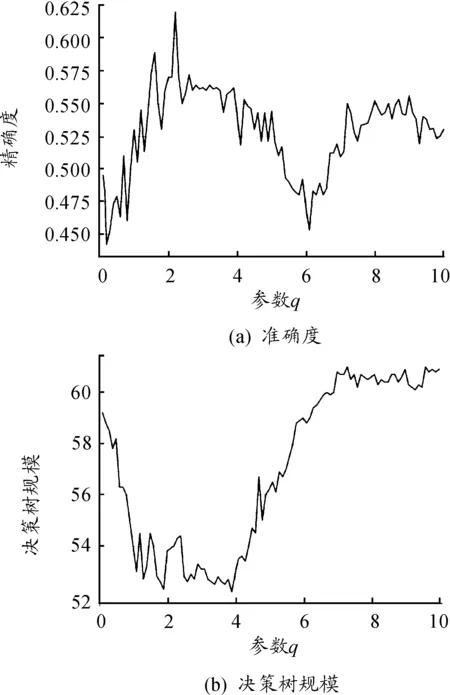
图1 不同q值在Abalone数据集上的测试结果

5 结束语

本文对决策树构建算法进行改进，提出Tsallis算法，将ID3、C4.5和CART统一起来，并通过调节q适应不同数据集，使Tsallis算法达到最优，同时结合“关键度度量”类标识标准，解决了数据集中小类属被忽略的缺陷，以此方法构建的决策树更加完美，不但准确度高，而且决策树规模较小。实验分为两个部分：第1部分比较了Tsallis算法与传统属性分割方法构建决策树准确度和树规模，验证了基于Tsallis算法构建决策树性能的提高；第2部分在Tsallis算法基础上引入了“关键度度量”并与Tsallis算法构建决策树进行比较，准确度和树规模均取得了更好的效果。经过两部分的实验，循序渐进地验证了本文提出的改进措施，下一步研究重点为如何快速求得最佳参数q和进一步降低构建树的时间复杂度。