重载AGV车辆跟踪算法和运动特性研究

吴宁强，李文锐，王艳霞，翟兆阳

(1.西安航空学院 汽车检测工程技术研究中心， 西安 710077； 2.北京无线电计量测试研究所， 北京 100854; 3.西安交通大学， 西安 710048)

自动导引车(automatic guided vehicle, AGV)是一种无人驾驶的导引运输车。AGV系统涉及机械、电子、光学、计算机等多个领域。近些年来，重载AGV车辆逐渐应用于不同的场合，在生产过程中发挥着重要的作用，尤其在汽车生产线上，可大大提高运转效率、精度，减少人力和劳动成本[1-3]。

AGV小车控制系统分为导引、通讯、驱动、供电、安全与辅助5大模块。其中AGV小车导引单元按导引方式大致为磁导引、光学导引以及惯性导引，AGV小车通过导引单元捕捉路面相关提示信号(磁信号、光学信号等)，将这一信号传递给主控单元PLC，PLC处理信号后向驱动单元的伺服电机发送命令使电机做出调整，从而使AGV小车在规定的路径上行驶[4-5]。

本文以双舵轮驱动转向的AGV小车为研究对象,建立的模型如图1所示。它的底盘部分由前、后桥的舵轮机构和从动万向轮组成，每个舵轮兼顾驱动和转向2个功能，舵轮的驱动和转向由4个直流伺服电机控制。转向舵轮支架旁外挂1个无接触起电感应器，为了保持平衡起电器支架旁安装1个万向轮支撑。小车还安装有4个从动万向轮，这些从动轮负责承载车架负载和保持平衡。

图1 建立的双舵轮AGV模型

1 AGV导引与轨迹跟踪

1.1 AGV单舵轮转角运动模型和定位算法

AGV导航需要知道自己相对于环境坐标系下的精确坐标。而对于坐标的寻找离不开定位算法。在舵轮驱动AGV的寻位原理和算法中所有模型均建立在如下几点假设上：

1) AGV车身看成刚体。

2) AGV舵轮与其他行走轮间机械结构不计摩擦阻力，忽略车体的惯性阻力和惯性力矩。图2为运动解析图。

图2 单舵轮AGV运动解析图

在单舵轮AGV运动模型中，给前舵轮1个转向角α，设前舵轮的速度为V， AGV小车会绕O点做转动。设角速度为ω，前后中心点O1、O2到AGV小车转动瞬心O点的距离分别为R1、R2。O1、O2之间距离为h，设AGV前进方向与X轴正向(逆时针为正)的夹角为β。小车逆时针转动时α取正值，反之取负值。设Vx、Vy分别为后轮中心点O2速度的水平分量和竖直分量，初始时刻为0 s，小车初始方向角为β0，则位置坐标x和y如下：

(1)

(2)

β=β0+ω×t

(3)

Vx=V×cos(α)×cos(β)

(4)

Vy=V×cos(α)×sin(β)

(5)

1.2 AGV双舵轮转角运动模型和定位算法

在双舵轮AGV转弯时两轮都产生1个转动角度，如图3所示。

图3 双舵轮AGV运动解析图

设前舵轮转过α1，速度为V1。后舵轮转过α2，速度为V2。小车转动瞬心为O，前舵轮中心为O1，后舵轮中心为O2，O1和O2的距离为h，角速度为ω,现在通过观察ΔO1OO2得

∠O1OO2=α1+α2

(6)

根据正弦定理得：

(7)

AGV小车转弯行驶时间为t，u为积分变量。Xr、Yr为后舵轮轨迹坐标，Xf、Yf为前舵轮轨迹坐标，X0、Y0为前后舵轮连线中点的轨迹坐标，将其设为小车的轨迹参考点。则坐标公式为：

(8)

(9)

(10)

(11)

(12)

(13)

这样AGV结合2种算法和舵轮速度与转角编码器的信号就可以知道AGV任意时刻前轮和后轮的坐标位置信息和方向角信息。现在将前后舵轮中点坐标(X0，Y0)视为AGV轨迹参考点。

1.3 AGV算法部分曲线运动轨迹和转弯动力学稳定性分析

通过建立的AGV运动学模型，代入相关参数，通过Matlab拟合双舵轮AGV在汽车厂的运动路线。图4为建立的双舵轮和单舵轮AGV的理论1/4圆弧轨迹模拟，控制AGV单舵轮转角为20°，速度为1.41 m/s；双舵轮AGV前、后舵轮同步转过20°，舵轮速度为1.41 m/s。单舵轮小车参考点速度为1.32 m/s，角速度为0.205 rad/s；双舵轮小车速度为2.65 m/s，角速度为0.820 rad/s。其转弯半径分别为单舵轮6.87 m，双舵轮3.435 m，双舵轮的转弯半径明显小于单舵轮小车。

由单舵轮和双舵轮的理论轨迹可见：单舵轮转弯半径较大，而且转弯时后轮往往要与地面产生滑动摩擦，增大了零件的磨损和行驶阻力；双舵轮驱动的AGV在路径转弯上轨迹良好，车轮与地面为滚动摩擦，在一些特定场合，双舵轮AGV车辆会采用子午线轮胎，其横摆角速度和稳定性对AGV的运行非常重要。图5为双舵轮AGV的转弯动力学分析。

图4 单、双舵轮1/4圆弧参考点理论轨迹

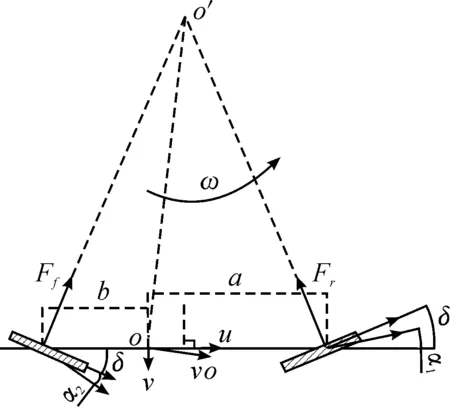
图5 双舵轮AGV转弯动力学分析

为了便于分析，模型简化为线性二自由度的双舵轮车辆模型，并做如下假设：

1) 重载AGV车厢只做相对于地面的平面运动。忽略悬架对AGV小车的影响[6]。

2) 沿X轴方向速度u保持不变，AGV小车侧向加速度在0.4g范围内[7]。

3) 驱动力不大，不考虑对轮子侧偏特性的影响和忽略回正力矩的影响。

图5中：m为车辆质量，m=2 000 kg；a、b分别为质心到前后舵轮中心点的距离，a=1.6 m，b=0.9 m；k1和k2分别为前后轮侧偏刚度，k1= -52 618，k2= -110 185；v0为质心速度，u为质心速度沿小车前、后舵轮中心点连线方向上的分量，其大小为1.5 m/s，v为质心速度垂直于小车前后舵轮中心点连线的分量，前后舵轮转角为δ0，大小为π/6，β=ν/μ，小车绝对加速度沿轴OY的分量为

(14)

前后轮侧偏角：

β-δ

(15)

(16)

进一步得到AGV小车转弯的单自由度强迫振动微分方程：

(17)

其中：ω0为固有圆频率，大小为41.583 9 rad/s；ζ为阻尼比，大小为1.038 7；常数B0=2 078.9。利用Matlab对上述微分方程求解，结果如图6所示。

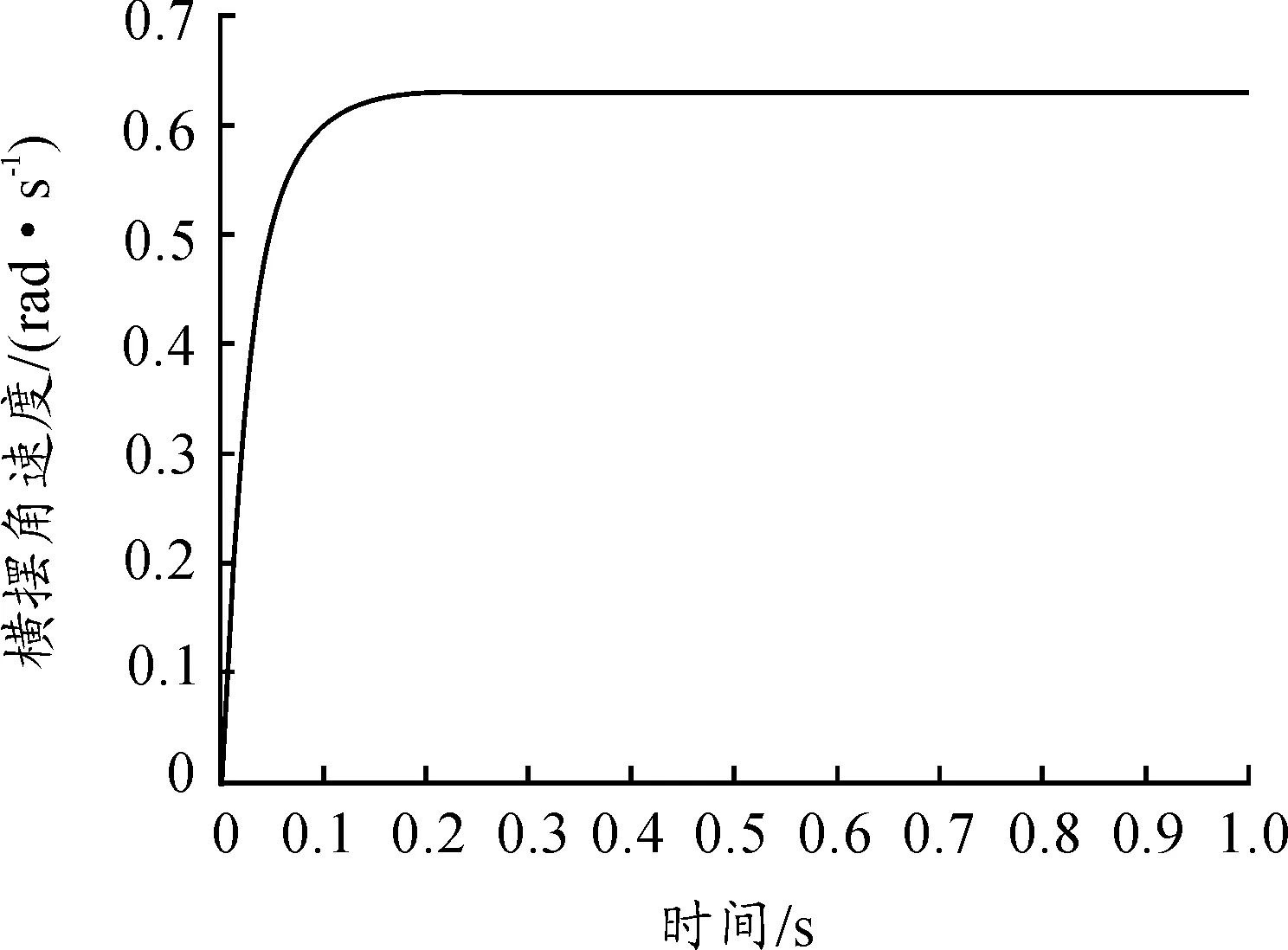
图6 横摆角速度仿真

在角阶跃δ下，横摆角速度是一条单调递增逐渐趋近于稳态角速度的大阻尼曲线[8]，其中稳态角速度和稳定因数为：

×δ0×m0)/c

(18)

(19)

代入参数得稳定因数K=8.266 8×10-4，稳态角速度为0.629 5 rad/s,由于K>0且转向角速度收敛于稳态角速度，所以双舵轮AGV的稳态转向为不足转向特性[9]，是一种稳定情况且角速度响应迅速。衡摆角速度增益

(20)

运用Matlab仿真稳态横摆角速度增益，结果如图7所示。

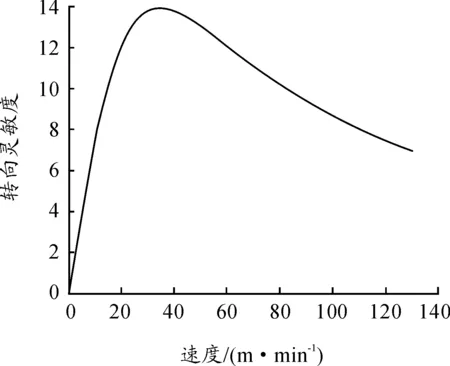
图7 稳定因数仿真

因衡摆角速度需要一定时间才能到达稳态值，而这段时间小车也在运动，所以实际转弯轨迹与理论转向轨迹不同，其中小车角速度稳定时间为0.3 s时，重载AGV车辆角速度才趋近于稳定状态，因而理论与实际车辆轨迹会出现一定误差。图8为利用Matlab对理论与实际误差的模拟情况。红色为理论转向轨迹，黑色为实际轨迹，其中理论转弯与实际转弯的圆心坐标X轴精度为 0.018 7 m，Y轴精度为0.026 8 m。

图8 重载AGV 1/4圆轨迹

2 AGV转弯误差分析及补偿

前面分析了AGV的转弯稳定性，而重载AGV转弯时不光存在角速度失稳的情况，实际上由于电机的响应问题会造成小车转弯的理论轨迹与实际轨迹发生偏差。以下对这一偏差进行分析。实验用双舵轮AGV小车部分参数如下：轮距L=2.5 m,额定转速为2 200 r/min，速度比为1∶100，最大角加速度为46 rad/s2,最大角速度为2.3 rad/s，电机加速时间为0.05 s，舵轮最大转角为±60°，AGV小车设定转角为33°，车速u=90 m/min。

为了分析需要把舵轮电机角速度响应分为3个阶段：匀加速、匀速、匀减速。利用近似离散化数值积分的方法对响应阶段进行分析，以0.025 s为最小时间参数分割。在Matlab环境下进行模拟。图9和10分别为AGV舵轮角度增加函数和角速度变化函数[10]。

图9 AGV舵轮角度增加函数

图10 AGV角速度变化函数

设AGV小车需要转过一个1/4圆弧段路径，这也是应用在汽车厂的常见路径。弯道起点坐标X=1,Y=1，在Matlab中对AGV参考点理论曲线和实际路线进行仿真(包括补偿后路径仿真)，结果如图11所示。

图中理论圆心坐标为(1，2.928 9)，实际圆心坐标为(1.209 5,2.931 1)，补偿后圆心坐标为(1.009 5，2.931 1)，补偿量为0.20 m，补偿前X轴误差为0.209 5 m，补偿前Y轴坐标误差为0.002 2 m，补偿后X轴误差为0.009 5 m，补偿后Y轴坐标误差为0.002 2 m。可以看出：通过控制AGV小车以X轴补偿量经过提前转弯，可以较大幅度地减小弯道处的轨迹误差。

图11 双舵轮AGV曲线路径

3 结论

1) 建立单、双舵轮的运动模型，通过Matlab计算单、双舵轮1/4圆弧参考点理论轨迹,双舵轮转向是一种较稳定的工况。

2) 通过对双舵轮AGV路径跟踪技术的研究分析，从动力学角度验证了其转向灵敏性和角速度对小车的影响，又从电机响应角度分析了AGV小车的轨迹误差存在的原因。

3) 通过控制AGV小车以X轴补偿量经过提前转弯，可以较大幅度地减小弯道处的轨迹误差。