弹性力学平面应力问题的加权残值法分析

宋国辉

（安徽建筑大学 土木工程学院，合肥 230601）

1 引 言

加权残值法又称为加权余量法，是一种近似方法，它在求解力学问题的时候，可以从微分方程式直接解出近似解。

它在流体力学、热传导以及化学工程等方面应用较为广泛［1］。

2 加权残值法的基本内容

对于工程科学类的问题，最终的求解都可以把它看成在给定的初始条件下求解微分方程式（组）。如有某问题的控制微分方程及边界条件为:

其中ζ为待定函数，D、H为微分算子，d、h为已知函数，m为边界条件数。

要求上述的控制方程，可以直接假定待定函数ζ的一个近似解，即试函数Γ:

式中Ck为待定系数，Nk为已知的试函数，n为试函数的数目。

通常情况下，将试函数代入上述控制方程和边界条件，试函数Γ一般不会符合要求，那么便产生了内部和边界残值，分别为Ra、Rb，

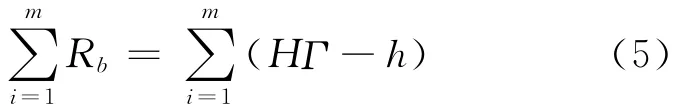
可以采用内部权函数Wa和边界权函数Wb来消除残值，则对应的方程为:

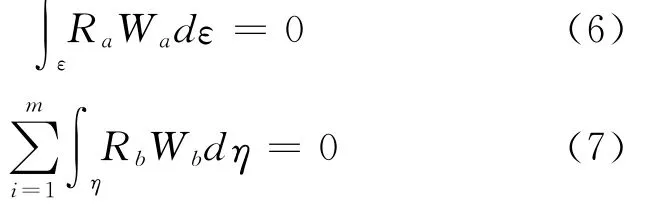
通过计算，解得待定系数Ck（k＝1，2…n）。将Ck代入试函数方程，得问题的近似解。

根据权函数的不同，加权残值法计算可以分为以下几种:

① 最小二乘法

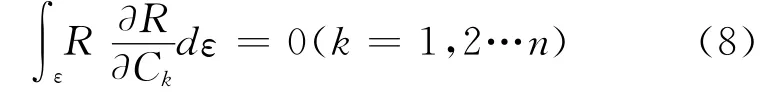
可以求得待定系数Ck。

② 配置法

配置法包括配点法，配线法，配面法及配域法等，这里只介绍配点法。

权函数为笛拉克δ函数:

二维问题:

通过解（10）得Ck。

③ 伽辽金法

按加权残值法的观点去理解伽辽金法，伽辽金法实际上就是将试函数项当做权函数的加权残值法［2］。

④ 子域法

将物体的ε域分为n个子域εk（k＝1，2，3…n），权函数满足Wk＝1（在εk内），Wk＝0（不在εk内）。则残值方程组为:

即可求得Ck。

⑤ 矩量法

二维问题:

求解方程（12）可求得待定系数。

3 平面应力问题

求解平面应力问题时，应满足应力函数φ（x，y）表示的相容方程:

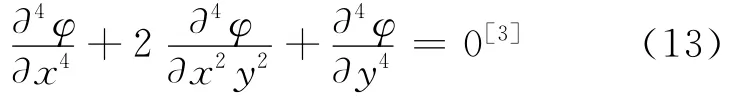
上式可以简化为

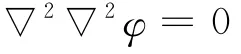
应力边界条件:

其中X，Y为给定的面力分量，l，m为外法线的方向余弦。

在弹性力学中，应力分量和应力函数φ（x，y）之间满足的条件为:

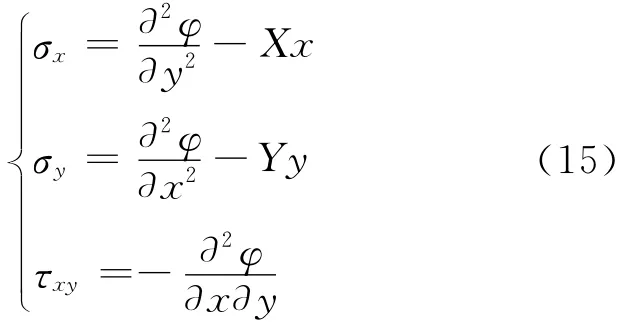
其中Xx，Yy，Xx，Yy代表的是体力分量。那么，求解平面应力问题就变成了求解满足（13）和（14）的应力函数φ（x，y）。

4 算 例

4．1 以三角形悬臂梁为例，说明该方法的应用。

如图1所示，为一个只受重力作用的三角形悬臂梁，梁的密度为ρ，求其应力分量。

图1 三角形悬臂梁

对于该题我们用加权残值法中的配点法求解，则:

（1）应力边界条件:

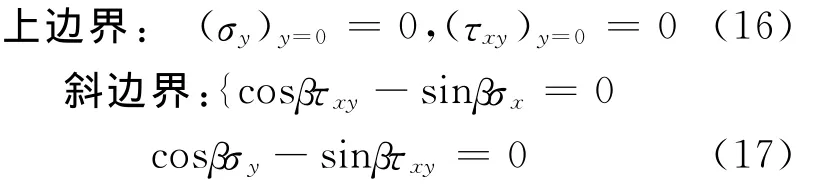
（2）试函数

三角形悬臂梁的应力分量由重力组成，则取试函数为:

（3）配点法求解

显然（18）满足相容方程（13），则取上边界任一点（x，y＝0）及斜边界上一点（1，tanβ）进行配点。将试函数代入（15）可得:

将式（19）代入上边界（16）得残值方程为:

以上边界任意一点（x，y＝0）代入上式，解得a＝0，b＝0将式（19）代入斜边界（17）得残值方程为:

将a＝0，b＝0及斜边界上任意一点（1，tanβ）代入上式残值方程解得

将上 面 解 得 的a，b，c，d代 入 （19）得，

下面我们再以一端固定的细长杆为例，来说明该方法的应用。

如图2所示，一端固定的细长杆，在长边界受均匀分布力q，试求解应力分量。

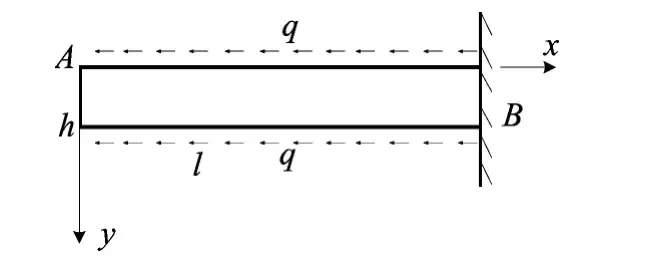
图2 一端固定细长杆

对于该问题可以用加权残值法中的最小二乘法求解。

（1）应力边界条件:

上边界:

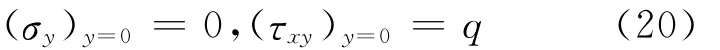
下边界:

左边界:

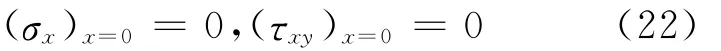
（2）试函数

应力分量由多项式解答，则取试函数为:

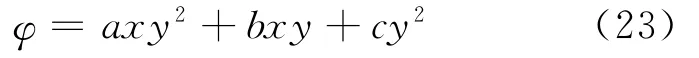
（3）最小二乘法求解

显然（23）满足相容方程，将（23）代入（15）得

将式（24）代入上边界得残值方程为:

将式（24）代入下边界得残值方程为:

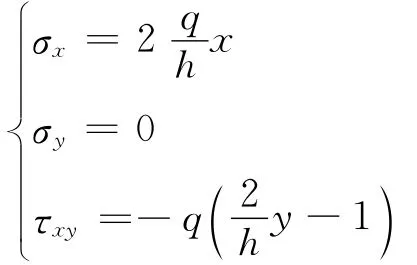
那么解答结果与弹性力学也是相同的。

5 结 论

本工作利用加权残值法中的基本理论知识，用配点法分析了三角形悬臂梁，用最小二乘法分析了一端固定的细长杆，通过分析得出的数值解，并与弹性力学的解析解比较，两者结果是一致的。因此，可以看出该方法在实际使用中的简单，易操作性。

1 徐文焕，陈虬．加权余量法在结构分析中的应用［M］．北京:中国铁道出版社，1985:1－2．

2 徐次达，陈学潮，郑瑞芬．新计算力学加权残值法－原理、方法及应用［M］．上海:同济大学出版社，1997:2－5．

3 徐芝纶．弹性力学简明教程第三版［M］．北京:高等教育出版社，1990:30－40．