关注倍角模型，破解中考压轴题*——等腰三角形中的两个倍角关系模型在解题中的应用

☉宁夏中卫市沙坡头区宣和镇张洪学校 张 宁

一、模型呈现

如图1，在△ABC中，AB=AC，BD⊥AC，垂足为D，∠BAE是顶角∠BAC的外角，则：

（1）∠BAC=2∠DBC，即等腰三角形一腰上的高与底边的夹角等于顶角的一半；

（2）∠BAE=2∠ABC=2∠ACB，即等腰三角形顶角的外角等于一个底角的两倍.

证明：（1）如图2，过点A作AF⊥BC，垂足为F，则∠FAC+∠ACB=90°.

由等腰三角形“三线合一”的性质，可知AF平分∠BAC，即∠FAC=∠BAC.

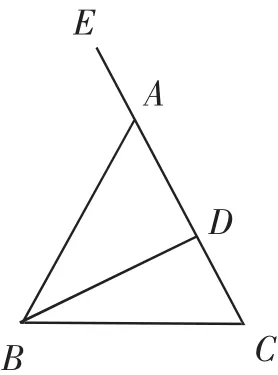
图1

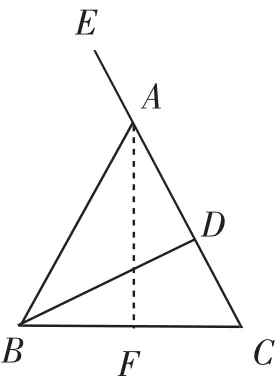
图2

由BD⊥AC，可知∠BDC=90°，所以∠DBC+∠ACB=90°.

由“同角的余角相等”，可知∠FAC=∠DBC，所以∠DBC=∠BAC，即∠BAC=2∠DBC.

说明：图1给出的等腰△ABC是锐角三角形，当等腰△ABC是钝角三角形时，结论依然成立；当等腰△ABC是直角三角形时，结论显然成立.

（2）利用等腰三角形及三角形外角的性质容易证明，此处从略.

这是等腰三角形中两个重要的倍角关系，利用这两个倍角关系可破解中考压轴题.

二、模型应用

例1（2018年江苏省扬州市）如图3，四边形OABC是矩形，点A的坐标为（3，0），点C的坐标为（0，6），点P从点O出发，沿OA以每秒1个单位长度的速度向点A运动，同时点Q从点A出发，沿AB以每秒2个单位长度的速度向点B运动，当点P与点A重合时运动停止.设运动的时间为t秒.

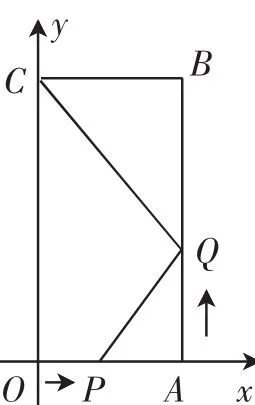
图3

（1）当t=2时，线段PQ的中点坐标为_______.

（2）当△CBQ与△PAQ相似时，求t的值.

（3）当t=1时，抛物线y=x2+bx+c经过P、Q两点，与y轴交于点M，抛物线的顶点为K，如图4所示.问：该抛物线上是否存在点D，使∠MQD=∠MKQ？若存在，求出所有满足条件的D点的坐标；若不存在，请说明理由.

解析：（1）当t=2时，OP=2，AP=1，AQ=4，所以P（2，0）、Q（3，4）.

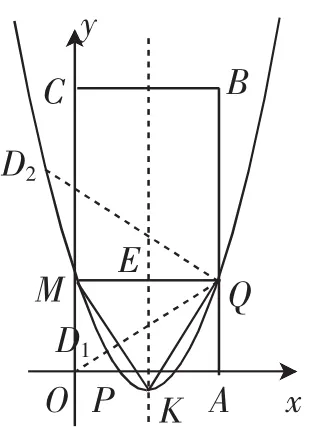
图4

（2）由已知条件易知PA=3-t，AQ=2t，BQ=6-2t.

△CBQ与△PAQ相似有两种情况，利用相似三角形的性质列方程易求得答案.请有兴趣的读者自行探究，限于篇幅，此处从略.

（3）当t=1时，易求得P（1，0）、Q（3，2）.将其代入y=x2+bx+c，得所以抛物线的解析式为y=x2-3x+2，从而可得点M的坐标为（0，2）.又因为Q（3，2），即点M与点Q的纵坐标相等，所以MQ∥OA.因为）是抛物线y=x2-3x+2的顶点，由二次函数的对称性易知△KMQ是等腰三角形，KM=KQ，∠MKQ是等腰△KMQ的顶角.根据等腰三角形中的倍角关系“等腰三角形一腰上的高与底边的夹角等于顶角的一半”，可知过点Q作KM的垂线，交抛物线于点D1，则∠MQD1=∠MKQ，如图4所示.

如图4，作抛物线y=x2-3x+2的对称轴，交MQ于点E.

由等腰三角形的性质，易知∠EKQ=∠MQD1，故tan∠MQD=tan∠EKQ=.又因为MQ=3，OM=2，所以易1知直线QD1经过原点O.利用待定系数法易求得直线QD1的表达式为y=x.

如图4，作直线QD1关于直线MQ的对称直线，得到直线QD，点D在抛物线上.易求得直线QD的解析式为y=-x+4.222

点评：本题是函数、方程、三角形的综合性问题，主要考查一次函数的性质、二次函数的性质、相似三角形的判定和性质、一元二次方程的解法、待定系数法等知识点，这些知识点是《义务教育数学课程标准（2011年版）》规定的最基础、最核心的内容.本题涉及的知识点比较多，承载着较强的中考选拔性功能.本题综合性较强，求解过程比较复杂，对学生而言具有很强的挑战性.解决问题（2）的关键是用t表示出有关线段的长度，再利用相似三角形的性质即可找到相关线段之间的关系，通过列方程即可解决问题.对于问题（3），这是一个倍角或半角关系的存在性问题，解决本题的难点是将倍角关系转化为等角关系，确定点D所在的直线，然后利用相似三角形或三角函数、一次函数、一元二次方程等知识求解.等腰三角形中的倍角关系模型在本题求解过程中发挥了重要作用，为本题的解决指引了具体的操作方向，这也是几何模型在解决问题过程中发挥作用的基本方式.确定点D1的坐标后，根据对称性在图4中易作出点D2，利用相同的方法可求出点D2的坐标.从求解过程可以看出，立足基本图形，深刻理解基本图形的性质，对分析问题和解决问题具有非常重要的引领作用.

例2（2018年河南省）如图5，抛物线y=ax2+6x+c交x轴于A、B两点，交y轴于点C.直线y=x-5经过点B、C.

（1）求抛物线的解析式.

（2）过点A的直线交直线BC于点M.

①当AM⊥BC时，过抛物线上一动点P（不与点B、C重合），作直线AM的平行线交直线BC于点Q，若以点A、M、P、Q为顶点的四边形是平行四边形，求点P的横坐标；

②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M的坐标.

解析：（1）由一次函数的性质易知点B的坐标为（5，0），点C的坐标为（0，-5）.将其代入y=ax2+6x+c，得解得所以抛物线的解析式为y=-x2+6x-5.

②如图6，∠ACB是定角，点M在直线BC上.由已知，直线AM与直线BC的夹角等于∠ACB的2倍，则∠AMB=2∠ACB或∠AMC=2∠ACB.由等腰三角形顶角的外角与底角的关系，易知构造等腰三角形，使∠ACB是等腰三角形的底角，∠AMB或∠AMC是这个等腰三角形顶角的外角.根据图形特征，显然△AMC是等腰三角形，∠AMB是这个等腰三角形顶角的外角.

如图6，作线段AC的垂直平分线，交AC于点D，交直线y=x-5于点M1，连接AM1，则△ACM1是等腰三角形.由此可知，∠AM1B=2∠ACB.以点A为等腰三角形的顶角的顶点，以AM1为等腰三角形的腰构造另一等腰三角形，落在直线BC上的顶点为M2，∠AM2C=2∠ACB.从而可知，满足条件的点M有两个.

如图6，过点M1作x轴的垂线，垂足为F，过点C作直线FM1的垂线，垂足为E，过点M2作x轴的垂线，垂足为G.

易知A（1，0）、C（0，-5）.令M1（m1，m1-5）、M2（m2，m2-5），则AF=m1-1，FM1=5-m1，CE=m1，EM1=m1，GM2=5-m2，AG=m2-1.

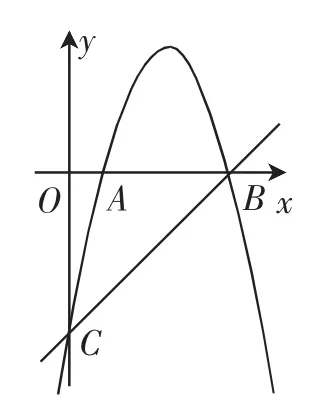
图5

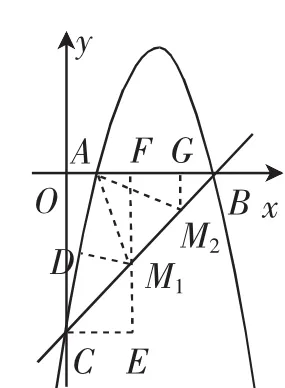
图6

由AM1=CM1及勾股定理，可知AF2+FM12=CE2+EM12.

所以（m1-1）2+（5-m1）2=m12+m12，解得m1=，故

由AM1=AM2及勾股定理，可知AF2+FM12=AG2+GM22，

综上所述，当直线AM与直线BC的夹角等于∠ACB的2倍时，点M的坐标为

点评：本题主要考查一次函数的性质、二次函数的性质、平行四边形的判定和性质、一元一次方程、一元二次方程、勾股定理、等腰三角形的性质与判定等知识点.本题涉及的内容比较多，综合性较强，求解过程比较复杂，对学生而言具有很强的挑战性.在问题（2）中，问题①是平行四边形的存在性问题，这是中考数学压轴题中最常见的一类问题，解决这类问题通常需要借助平行四边形的判定与性质，列方程求解；或借助中点坐标公式，直接利用“平行四边形对角顶点的横（纵）坐标之和相等”这一结论求解；问题②是倍角关系的存在性问题，根据图形的基本特征，解决本题的难点是将问题中的倍角关系转化为等腰三角形顶角的外角与底角之间的关系，然后借助勾股定理列方程求解.等腰三角形顶角的外角与底角之间的倍角关系模型在本题求解过程中发挥了引领作用.确定点M1的坐标后，借助对称性或辅助圆在图6中易作出点M2，利用相同的方法可求出点M2的坐标.

说明：由于初中学生未曾接触平面直角坐标系内两点之间的距离公式，所以问题②借助勾股定理列方程求解.当然，对于教师而言，本题还可以先求出直线DM1的解析式，然后联立方程求解.

三、解题反思

1.关注基本图形和几何模型

图形与几何是初中数学中非常重要的内容，在近几年各地中考试题中，将几何图形与函数图像融合的压轴题屡见不鲜，这类试题所涉及的知识点较多，综合性强，对学生而言极具挑战性.笔者认为，所有与几何图形有关问题的解决，几乎都要回归到基本图形的性质，只有熟练掌握基本图形的性质，深刻理解基本图形的性质在解题中发挥作用的方式，才能得心应手地运用基本图形解决相关数学问题，才能不断提高学生的几何推理能力.因此，在图形与几何教学中，教师要不断引导学生建立数学模型思想.其一，不仅要让学生熟练掌握平行线、角平分线、中线、高线、垂直平分线、等腰三角形、直角三角形、平行四边形、矩形、菱形、正方形、等腰梯形、圆等基本几何图形的性质，而且要理解这些基本几何图形的性质在解决问题中的作用与应用方式；其二，全等三角形与相似三角形也是非常重要的几何模型，不仅要理解它们的性质与判定，而且要学会运用它们解决实际问题；其三，要让学生熟练掌握平移、轴对称、中心对称、旋转等基本图形变换的性质及其在解题中的作用.

2.发挥几何模型的解题引领作用

如果学生熟练掌握基本几何图形的性质，内化为自身的几何素养，在解决相关数学问题时，就能准确找到与之对应的几何模型，然后采取行之有效的解题方法与策略，从而为考试节省不少时间.笔者认为，解决问题的过程中，虽然不宜直接利用几何模型的相关结论，但几何模型能够为解题指引正确的方向，合理地使用几何模型能使原本复杂的问题变得简单易解，使学生少走弯路，从而提高学生分析问题和解决问题的能力.

四、结束语

《义务教育数学课程标准（2011年版）》指出，在数学课程中，应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想.王尚志教授曾指出，学生在数学学习中应培养“数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析”这六大核心素养.推理能力是数学思维能力的重要组成部分，几何推理是培养学生推理能力的重要载体.因此，几何推理能力对学生而言至关重要.波利亚曾说过：“掌握数学就意味着善于解题.”解题是数学学习活动的基本形式，也是学生参与数学学习活动的主要内容.因此，数学学习离不开解题.波利亚在其著作《数学的发现——对解题的理解、研究和讲授》中认为：“解题是一种本领，就像游泳、滑雪、弹钢琴一样，你只能够靠模仿和实践才能学到它”“中学数学教学的首要任务就在于加强解题训练”.笔者认为，在数学学习中，教师要引导学生善于归纳总结基本几何模型，形成模型思想，这是培养初中生几何推理能力的有效途径之一.