乘法公式单元教学起始课教学研究

☉江苏省邗江中学（集团）北区校维扬中学 谈 兵

现行初中数学教材关于整式乘法中的乘法公式教学都是逐个进行，先学习平方差公式（a+b）（a-b）=a2-b2、完全平方公式（a±b）2=a2±2ab+b2，再在教材的习题训练中渗透（x+a）（x+b）=x2+（a+b）x+ab这个公式.最近我们在研习著名特级教师李庾南老师关于单元教学相关教学思想时，对李老师倡导基于数学知识内在联系进行“学材再建构”的主张产生共鸣.在最近一次教研活动中，笔者开设了一节乘法公式单元教学起始课，取得了较好的教学效果.本文梳理该课的教学流程，并给出教学立意的阐释，供研讨.

一、乘法公式单元教学起始课教学流程

说明：本课是在学生已学习整式乘法之后进行的新授课教学，学生对多项式乘以多项式也已训练到位.

教学活动（一） 从“（x+a）（x+b）”出发

例1计算下列各题：

（1）（x+1）（x+2）；

（2）（x-2）（x-3）；

（3）（x+3）（x-5）；

（4）（x-10）（x+9）.

教学预设：学生很快能算出4个小题的答案：x2+3x+2，x2-5x+6，x2-2x-15，x2-x-90.

解后问题1：这4个结果都是二次三项式，同学们观察一下，各项系数与原来两个一次二项式之间有怎样的对应关系？你们能用字母表示吗？

教学预设：学生答出（x+a）（x+b）=x2+（a+b）x+ab后，安排他们证明这个性质.也就是将（x+a）（x+b）展开得4项后，再合并成x2+（a+b）x+ab.证明之后小结为“乘法公式1”，板书在黑板主板区.

解后问题2：小组内再用几个例子验证一下上面的发现！

【跟进练习1】

（1）（x+42）（x-2）=__________；

（2）若（x+3）（x+b）=x2+4x+c，则b=______，c=______；

（3）若（x+5）（x-m）展开后不含有关于x的一次项，则m=______；

（4）若（x-4）（x+b）=x2-8x+c，则b=______，c=______.

设计意图：前两题主要是训练刚刚小结的“乘法公式1”，后两题变式训练“乘法公式1”，并对应着后面即将要学习的平方差公式、完全平方公式.

教学活动（二） “（x+a）（x+b）”中常数a、b互为相反数

例2已知（x+a）（x+b），其中a、b为非零实数，根据下列条件计算：

（1）当a=1，b=-1时，（x+a）（x+b）=__________.

（2）当a=-2，b=2时，（x+a）（x+b）=__________.

（3）当a=m，b=-m时（m为非零实数），（x+a）（x+b）=__________.

（4）小婧发现：当a+b=0时，计算（x+a）（x+b）的结果只有两项.你觉得小婧的发现是否正确？请说明理由.

教学预设：前面3题的结果依次为x2-1、x2-4、x2-m2.小婧的发现是正确的.可以使用“乘法公式1”说明.

（x+a）（x+b）=x2+（a+b）x+ab，而a+b=0，则（x+a）（x+b）=x2+0·x+a（-a）.

即（x+a）（x-a）=x2-a2.

证明之后，学生小结出“乘法公式2”，即平方差公式：（a+b）（a-b）=a2-b2.教师板书在黑板主板区.

【跟进练习2】计算：

（1）（3x+2）（3x-2）；

（2）（-m+2n）（-m-2n）；

（3）（x+2）（x-2）-（x-1）（x+5）；

（4）98×102.

设计意图：对于（1）和（2），直接套用平方差公式即可；第（3）题需要分别使用平方差公式、乘法公式1简化运算；第（4）题需要改写变形后使用平方差公式简化计算.

教学活动（三） “（x+a）（x+b）”中常数a、b相等

例3已知（x+a）（x+b），根据下列条件计算：

（1）当a=b=1时，（x+a）（x+b）=__________；

（2）当a=b=-2时，（x+a）（x+b）=__________；

（3）当a=b=9时，（x+a）（x+b）=__________；

（4）通过以上计算，你能发现一个“乘法公式”吗？

教学预设：前面3题的结果依次为x2+2x+1、x2-4x+4、x2+18x+81.在此基础上，引导学生自主归纳出“乘法公式3”，即完全平方公式：（a±b）2=a2±2ab+b2，教师板书在黑板主板区.

【跟进练习3】计算与思考：

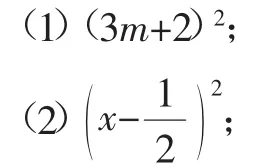
（3）1022；

（4）思考：（x+y）2与（-x-y）2是否相等？（x-y）2与（y-x）2是否相等？

设计意图：前3题可直接运用完全平方公式计算，第（4）题两种结果都相等，评讲时要注意引导学生与七年级学习有理数乘方时积累的互为相反数的两个数的平方相等这一性质x2=（-x）2对应起来.

教学活动（四） 完善乘法公式之间的框架体系

小结、梳理本课所学几个乘法公式之间的关系，完善它们之间的联系．“结构式”板书如下所示.

【跟进练习4】计算：

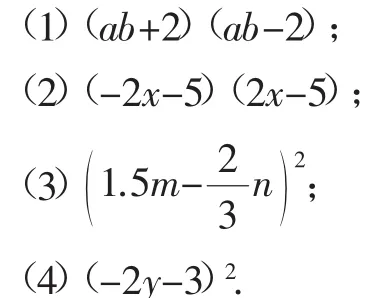
设计意图：第（1）和（2）题主要训练平方差公式，其中第（2）题在学生做出结果之后要注意通过追问暴露不同学生的解法，比较出最优方法，即将原式改写为（-5-2x）（-5+2x），再套用平方差公式计算；第（3）题引导学生将小数先化为分数，然后看清算式特点，选准完全平方公式进行计算；第（4）题也注意引导学生利用性质（x+y）2=（-x-y）2，将（-2y-3）2转化为（2y+3）2，在套用完全平方公式展开时避免多次处理负号.

二、教学立意的进一步阐释

1.从数学现实出发，基于条件变式引出新知

本课我们选择从简单的整式乘法出发，先通过一组计算题小结出“乘法公式1”，在跟进训练之后，将“乘法公式1”中的常数a、b赋予不同的强化条件“a+b=0”“a=b”，分别对应着后续即将探究的平方差公式、完全平方公式.这种新课引入方式没有创设所谓的生活情境，而是从数学现实出发，基于条件变式引入新课，也是当前值得重视的一种数学引入方式.需要指出的是，返璞归真，并不是简单的回归，而是基于对数学知识的深刻理解，践行《义务教育数学课程标准（2011年版）》所提出的要兼顾生活现实与数学现实引入新知的要求.当然，就本课新授内容而言，也是符合著名数学教育家张奠宙教授所提出的“超经验的数学”，即不需要引入所谓生活现实，而直接根据整式乘法运算的逻辑发展引出新知.

2.精心选编例、习题，围绕教学主题变式设问

有人曾把数学简言为两个字：算与证.本课属于“算”的内容，但也不能呆算、重复算，这就需要我们在选编各个教学环节的例、习题时，注意围绕各个教学环节的训练主题变式设问，而不是重复一些相同的算式类型.比如训练平方差公式的“跟进练习2”时，所选的4个题都对应着直接使用平方差公式，而不需“转多次弯”；再看课堂小结时所选编的“跟进练习4”中第（3）题和第（4）题，就进行了适当的改编，提高了要求，需要整体处理和改写变形.特别是，各个栏目下的训练题一定要围绕教学主题选编变式，注意聚焦训练目标，提高习题内容效度.

3.预设结构式板书，促进深刻理解乘法公式

最近两年《中学数学（初中版）》有不少课例文章都附出课时板书设计，有些“结构式”板书能加深我们对课例教学内容的深刻理解，对学生也是一种很好的示范.这也启发我们预设本课不同乘法公式之间关系的“结构式”板式.作为乘法公式单元教学起始课的教学，让学生通过结构式板书，知晓本单元所学内容的全貌，然后在后续习题课时，就可将习题训练的不同内容纳入到相应的知识体系之中，想来，这也是促进学生深刻理解乘法公式的一种教学努力.