A double inequality for the modulus of the Grötzsch ring in Rn

,

(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)

0 Notation and Main Results

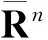
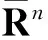
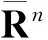
wheremis then-dimensional Lebesgue measure. By [1, Theorem 8.28, (8.31), (8.34) and (8.35)], the conformal capacity capRG,n(s) of the Grötzsch ringRG,n(s) can be expressed by

γn(s)≡capRG,n(s)≡M(Δ(Bn,[se1,∞])),

while the (conformal) modulus ofRG,n(1/r) is defined by

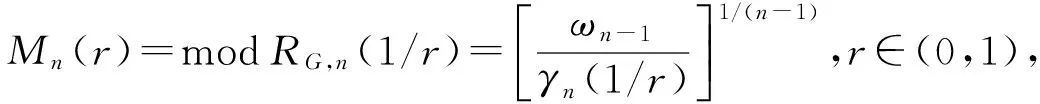
whereωn-1is the surface area of the unit sphereSn-1=∂Bn. Clearly,μ(r)≡M2(r) is exactly the so-called Grötzsch ring function, which has the following expression

(1)

where

The Grötzsch ring constantλnis defined by

which is indispensable in the study ofMn(r) andγn(s). It is well known thatλ2=4. Unfortunately, so far we have only known some estimates forλnwhenn≥3, among which is the following double inequality

2e0.76(n-1)<λn≤2en+(1/n)-(3/2),n≥3

(2)

(see [1, Theorem 12.21(1)] and [3]).

Now we introduce the gamma and beta functions, and some constants depending only onn, which are needed in the study of the properties ofMn(r) andγn(s). As usual, for complex numbersxandywith Rex>0 and Rey>0, the gamma and beta functions are defined by

respectively. (Cf. [4] and [5].) It is well known that, forn≥3, the volume Ωnof Bnand the (n-1)-dimensional surface areaωn-1ofSn-1can be expressed by

respectively. (Cf. [1, 2.23] and [6].) Let

In particular,

Some properties of Ωn,ωn-1,Jn,cnandAnwere given in [1, pp.38-44&163] and in [6].

In the sequel, we let arth denote the inverse function of the hyperbolic tangent tanh, that is,

During the past decades, many properties have been obtained forμ(r) (cf. [1]-[2] and [7]). The known properties ofMn(r), however, are much less than those ofμ(r), because of lack of effective tools for the study ofMn(r) whenn≥3. For example, we have no explicit expression as or similar to (1) forMn(r) whenn≥3. For the known properties ofMn(r) and its related functions, the reader is referred to [1], [3] and [7-13]. Some of these known results forMn(r) are related to the constantsλn,Ωn,ωn-1,Jn,cnandAn. For example, the following inequalities hold

(3)

(4)

(5)

forr∈(0,1) andn≥3 (see [1, Theorems 11.20(1), 11.21(2)&(4), and 11.21(5) ]).

h2(r)+h2(r′)=μ(r)μ(r′)≡π2/4

by [1, (5.2)]. It is well known that for eachn≥2, allr∈(0,1) and for allK>0,

φK,n(r)2+φ1/K,n(r′)2=1⟺Mn(r)Mn(r′)=const,

(6)

Later, [1, 11.36(2)] says that for eachn≥2 and allr∈(0,1),

(7)

However, the proof of the second inequality in (7) given in [1, p.244] contains an error. This proof in [1, p.244] is as follows: [1, Corollary 11.23(1) and (4) ] yield

and the upper bound in (7) follows, since [1, Theorem 1.25 ] implies that the function

合作学习应该建立在学生自主学习基础上，为进一步提升学生合作学习效率，作为中学教师要合理引导学生自主预学，使学生对本课学习内容形成初步认识。

is increasing from (0,1) onto (1,2 logλn). It is easy to see that by this “proof ”, one can only obtain the following inequality

so that the upper bound forhn(r)+hn(r′), which we can obtain by this method, is as follows

consisting with that in (6). So far, the known best upper bound forhn(r)+hn(r′) is given by (6).

In addition to indicating the error in the proof of (7) given in [1, p.244] as above-mentioned, the main purpose of this paper is to improve the upper bound given in (6) by proving the following result.

Theorem1Lethn(r)=r′2Mn(r)Mn(r′)n-1. Then for eachn≥2 and allr∈(0,1),

(8)

where

1 Proof of Theorem 1

The proof of Theorem 1 stated in Section 0 requires the following lemma.

1.1 A Technical Lemma

Lemma1a) Forr∈(0,1), letg(r)=r2/arthrandf(r)=g′(r)/r. Thenfis strictly decreasing from (0,1) onto (-∞,∞).

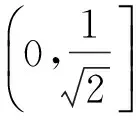
(9)

Proof:a) Differentiation gives

so that

(10)

Clearly,f(0+)=∞ andf(1-)=-∞. By differentiation,

(11)

b) It is easy to verify that

Then the remaining conclusions are clear.

1.2 Proof of Theorem 1

The first inequality in (8) was proved in [8, Theorem 5.1(3)].

LetH(r)=hn(r)+hn(r′), andFbe as in Lemma 1 b). By (5), we see that

(12)

On the other hand, the following inequality holds

Mn(r)

(13)

for eachn≥2 and all 0

is strictly decreasing from (0,1) onto (0,1) by [1, Theorem 11.21(4)]. It follows from (12) and (13) that

This, together with Lemma 1 b), yields

(14)

By (2), the following double inequality holds

(15)

where

This yields the second inequality in (8) as desired.

[1] Anderson G D, Vamanamurthy M K, Vuorinen M. Conformal Invariants, Inequalities, and Quasiconformal Maps[M]. New York: John Wiley and Sons,1997.

[2] Ahlfors L V. Lectures on Quasiconformal Mappings[M]. 2nd ed. American Mathematical Society,2005.

[3] Anderson G D, Frame J S. Numerical estimates for a Grötzsch ring constant[J]. Constr Approx,1988,4:223-242.

[4] Abramowitz M, Stegun I A(Eds.). Handbook of Mathematical Functions With Formulas, Graphs and Mathematical Tables[M]. New York: Dover,1965.

[5] Qiu S L, Vuorinen M. Handbook of Complex Analysis: Special Function in Geometric Function Theory: Volume 2[M]. Elsevier B V,2005:621-659.

[6] Qiu S L, Vuorinen M. Some properties of the gamma and psi functions with applications[J]. Math Comput,2005,74(250):723-742.

[7] Qiu S L. Grötzsch ring and Ramanujan’s modular equations[J]. Acta Mathematica Sinica,2000,43(2):283-290.

[8] Anderson G D, Qiu S L, Vamanamurthy M K. Grötzsch ring and quasiconformal distortion functions[J]. Hokkaido Math J,1995,24(3):551-566.

[9] Anderson G D, Vamanamurthy M K, Vuorinen M. Conformal invariants, quasiconformal maps, and special functions[M]//Quasiconformal Space Mappings. Berlin-Heidelberg: Springer-Verlag,1992:1-19.

[10] Anderson G D, Vamanamurthy M K, Vuorinen M. Inequalities for quasiconformal mappings in space[J]. Pacific J Math,1993,160:1-18.

[11] Ikoma K. An estimate for the modulus of the Grötzsch ring inn-space[J]. Bull Yamagata Univ Natur Sci,1967,6:395-400.

[12] Qiu S L, Vamanamurthy M K. Elliptic integrals and the modulus of Grötzsch ring[J]. PanAmer Math J,1995,5(2):41-60.

[13] Vuorinen M. On the boundary behavior of locallyK-quasiconformal mappings in space[J]. Ann Acad Sci Fenn Ser A I,1980,5:79-95.