低温条件下单层纺织材料孔隙率决定反问题
,,,2
(1.浙江理工大学 理学院,杭州 310018;2.上海财经大学 数学学院,上海 200433)
0 引 言
随着科技不断发展,人们对服装的要求不断提升,它不仅可以起到美观的效果,还具有防水、保暖、透湿等功能。近年来,如何优化服装性能,使其在恶劣环境下为人类提供保护、维持人体热湿舒适性,是国内外学者研究的热点问题之一。采用数值方法来优化服装性能,可帮助服装面料设计者和生产商缩短研发周期、节省研发成本。
国内外许多学者研究了服装热湿传递问题。最初的研究很少涉及相变,如:Ogniewicz等[1]在只考虑热传导和对流的情况下,最先分析了当液相水处于一个摆动状态时,热湿传递过程中的冷凝;Shapiro等[2]对多孔面料中移动状态水的冷凝进行分析,发现可将其归结为一个快速稳定状态进行考虑;Murata[3]在考虑重力和对流所传递的热量的情况下,对温度达到100 ℃时纺织材料热湿传递中冷凝速率的变化进行了理论和实验研究;Bouddour等[4]考虑到纺织材料的吸湿性,利用周期性结构均匀化渐近的方法,分析了湿润状态下纺织材料热湿传递过程中水的蒸发和冷凝的现象;Fan等[5-7]结合热力学等物理规律,对织物内传导、辐射以及相变等进行相关探讨研究,建立了动态的织物热湿传递模型,并将数值结果与实验结果进行对比,发现两者结果比较吻合,从而说明初始时刻水的含量以及水的相变对整个热湿传递过程热量的传递影响很大。
热湿传递的正问题是根据织物热湿传递微分方程及其边界条件,来求出织物内部温度和水汽浓度的分布,而反问题是基于热湿传递数学模型和一定的设计目的,来反演织物的物理或几何性质。关于反问题的研究结果相对较少,主要研究有:Du等[8-9]在低温条件下,提出了一个包含热传导和辐射的纺织材料的热湿传递模型,根据织物的保暖性,即热量损失最少,来决定织物的最优孔隙率;Korycki[10]采用一个较简单的三层织物热湿耦合模型,根据服装的保暖性能来最优决定三层织物的厚度;Xu等[11-14]采用一个动态的热湿传递模型,根据服装热湿舒适性,即人体皮肤与服装内侧间的微气候区的舒适温度和湿度区间,来提出织物热湿传递参数决定反问题,该热湿舒适性区间只适合静止状态,当人体处于运动状态时,该舒适性指标不再适用,因此按此指标构造的反问题具有一定的局限性。本文以Fan等[6]提出的热湿传递模型为基础,以保暖透湿性最佳为目的,利用服装的透湿指数来构造反问题,从而决定纺织材料的最优孔隙率,并说明孔隙率取值对保暖透湿性的影响。
本文首先根据文献[6]改进了低温条件下纺织材料动态热湿传递数学模型,采用有限差分对该模型进行数值求解,并证明了数值解的存在唯一性;然后根据低温条件下服装的保暖透湿性,提出了决定纺织材料最优孔隙率的反问题;最后采用遗传算法进行数值计算,并与函数图形最优解进行对比,以验证遗传算法结果的可靠性。
1 正问题
本节给出由人体皮肤-织物-环境所组成的系统的一个动态热湿传递模型,然后采用有限差分法对其进行数值求解,并给出解的存在唯一性定理。
1.1 动态热湿传递模型
首先给出人体皮肤-织物-环境系统的一个动态热湿传递模型,如图1所示。该模型中,织物由内外层以及中间层织物构成。内层织物挨近人体皮肤,外层织物靠近外界环境。在整个系统中,内层织物和外层织物边界之间存在较大的温度差,因此在中间织物和内外层织物内均存在热量传递,如热传导、辐射等。由于内外层之间存在水汽的浓度差,因此能量也会伴随着水汽的扩散而变化。
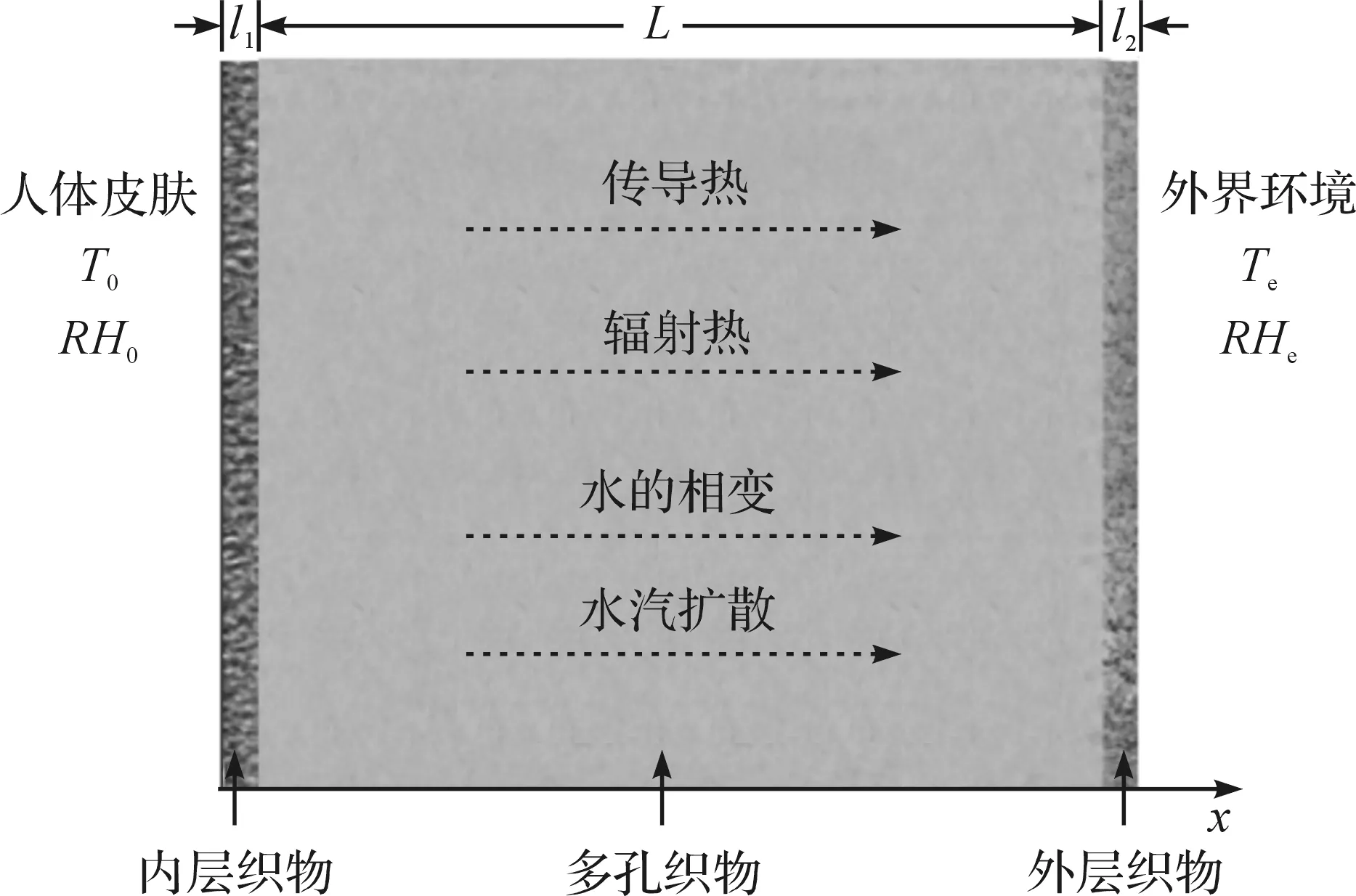
L表示中间织物厚度;l1表示内层织物厚度;l2表示外层织物厚度;T0表示人体皮肤温度;Te表示环境温度;RH0表示人体皮肤相对湿度;RHe表示环境相对湿度图1 人体皮肤-服装-环境系统
该模型基于如下假设:
a) 多孔织物内部纤维是同向性;
b) 忽略由水含量变化所引起的织物体积的变化;
c) 热湿传递模型中,不考虑外界的风速以及整个系统的对流热;
d) 相对中间织物纤维,两边织物层的厚度很小,可忽略不计。
由能量守恒定律、质量守恒定律,可得出如下织物内关于温度、水汽浓度以及辐射热耦合的偏微分方程组[13]:
(1)
式中:T(x,t)为织物内的温度;Ca(x,t)为织物孔隙间的水汽浓度;FL(x,t)和FR(x,t)分别为往左和往右所传递的热辐射;Γ(x,t)为水的相变速率;Cv(x,t)为织物体积热容量;k(x,t)为织物的等效热传导;λ(x,t)为织物相变的潜伏热系数;β为吸收常数;σ为波尔兹曼常数;ε为织物孔隙率;ζ为织物的曲折系数;Da为空气中水汽扩散系数;
ΩT:={(x,t)∈R2:x∈(0,L),t∈(0,Tt)};
Tt为总时间。
初始条件为:
(2)
关于辐射的边界条件为:
(3)
式中:ξ1、ξ2分别为织物的向左、向右辐射系数。
关于温度的边界条件为:
(4)
关于水汽浓度的边界条件为:
(5)
式中:T0、Te分别为人体皮肤、环境的温度;R0、R1分别为内层织物、外层织物的热阻;Ht为外层织物外表面与环境的对流热传递系数;Ca0、Cae分别为人体皮肤、外界环境的水汽浓度;w0、w1分别为内层织物、外层织物的湿阻;Hc外层织物外表面与环境的水汽传递对流系数。
文献[13]中,有关温度和水汽浓度的边界条件均为第一类边界条件,忽略了皮肤和织物内层间的微气候区。本文采用文献[6]中的第三类边界条件,既考虑了微气候区对织物中热湿传递的影响,又不受微气候区厚度的影响。
方程(1)中,热传导k(x,t)计算如下:
k(x,t)=εka+(1-ε)(kf+kw),
式中:ka为织物内空气的热传导,kf为织物纤维的热传导,kw为织物内水的热传导。
相变项Γ(x,t)满足如下偏微分方程:
(6)
其中:
(7)
为饱和水蒸汽浓度。式(8)中饱和水蒸汽压强Vap(T)是根据实验数据拟合而得,其计算公式[15]为:
(8)
织物内部和空隙之间的总含水量为:
(9)
式中:ρ为织物的密度。
此外,织物空隙间的相对湿度RH(x,t),可表示为:

(10)
结合初边值条件(2)—(5),通过求解热湿传递模型(1),得到织物内部温度和水汽浓度随时间、厚度变化的过程,称为正问题求解。
1.2 正问题的有限差分格式及解的唯一性
下面采用有限差分求解正问题。结合初边界条件,首先解耦方程(1),可得:
(11)
其中:
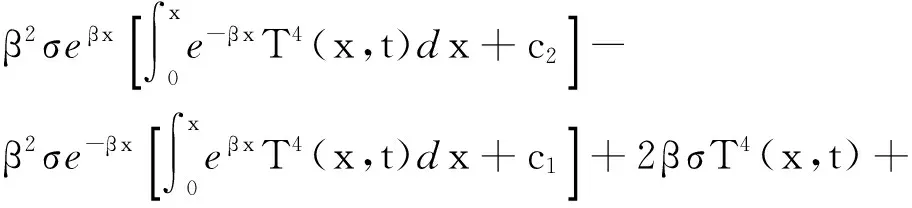
λ(x,t)Γ(x,t),



(12)
(13)
(14)
其中:

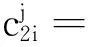
1≤i≤N-1,1≤j≤M-1.
最后,可得温度、水汽浓度的初边界条件的离散格式:
(15)
(16)
利用有限差分格式(12)—(16),可求得正问题的数值解,从而得到织物内部温度和水汽浓度的分布。
定理偏微分方程(1)的差分格式解存在且唯一。
证明:结合初边值条件(15)和(16),偏微分方程(1)的差分格式在j+1时刻关于温度的线性方程组为:
(17)
在j+1时刻关于水汽浓度的线性方程组为:
(18)
可利用数学归纳法证明线性方程组(17)解的存在唯一性。
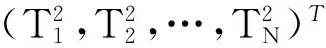
同理可证线性方程组(18)解的存在唯一性。
证毕。
1.3 正问题的数值模拟
下面给出一个正问题的数值例子。假定人体皮肤温度为35 ℃,相对湿度为96%;环境温度为-20 ℃,相对湿度为90%。织物的初始温度T0(x)=20 ℃。数值模拟参数值见表1和表2[7]。

表1 聚丙烯的参数值

表2 数值模拟参数值
结合表1、表2所给定的参数值,根据离散格式(12)—(16),可分别计算织物内部的温度和水汽浓度随时间、厚度的分布情况,如图2所示。由图2可看出,织物内的温度和水汽浓度从里到外随厚度的增加不断下降均沿厚度方向不断下降,这与实际情况相符。
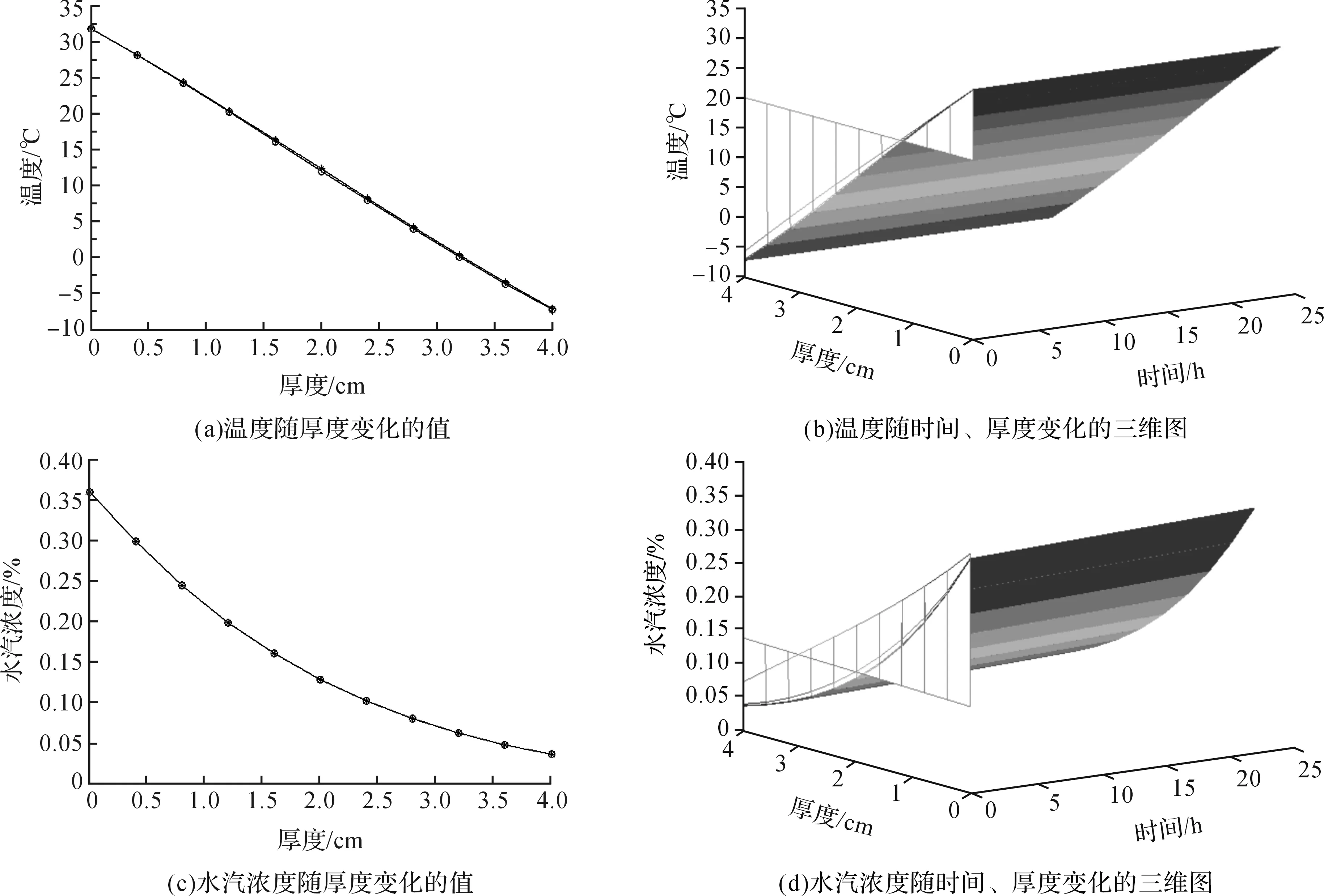
图2 织物内温度、水汽浓度分布
2 纺织材料孔隙率最优决定反问题
2.1 反问题的提法及对应的目标函数
服装的热湿传递性能主要依赖于一些物理或几何等参数,如纺织材料的厚度、孔隙率、曲折系数以及纤维的亲水性等。孔隙率是影响服装内水和能量传递的重要参数,相同材料不同孔隙率的服装可能具有完全不同的热湿性能。考虑到孔隙率的重要性,本文以织物的保暖透湿性为目的,来确定织物最优孔隙率。
Xu等[11-14]是根据服装热湿舒适性区间,即人体皮肤与服装内侧间的微气候区的舒适温度和湿度区间,来构造反问题。该热湿舒适性指标只适用于静止状态,具有一定的局限性。本文根据保暖透湿性最佳来构造反问题,用透湿指数这一指标来衡量织物保暖透湿性,其与热阻和湿阻的比值成正比[16]:
(19)
式中:Pi为织物透湿指数,S为湿度常数(0.015 K/Pa),Rt代表热阻,Rw代表湿阻,且有[17]:
(20)
式中:PS0、PSe分别为皮肤、环境处的饱和压强,Pe为环境处任意压强,RHe为环境任意相对湿度,Qdry、Qwet分别为干燥、湿润条件下的总热通量,MTol为总质通量。
低温条件下,当热阻不断变大时,织物散失的热量将逐渐减少,从而起到保暖的效果;当湿阻不断变小时,织物的通透性能逐渐增强,从而达到透湿的目的。因此,当热阻变大、湿阻变小时,透湿指数将随之增大,织物保暖透湿性也就越佳。本文根据透湿指数的最大值来最优决定孔隙率,从而保证织物的最佳保暖透湿性。
假设给定人体皮肤和外界环境的温度,及其相对湿度。织物的纤维孔半径、曲折系数等材料结构和导热系数等类型参数均已知。结合低温条件下纺织材料热湿传递模型,根据最大透湿指数来最优决定孔隙率,从而保证织物的最佳保暖透湿性。
根据上述提法,可构造反问题目标函数求解最优孔隙率ε*,使Pi(ε)达到最大值,即
(21)
根据热湿传递的规律及傅里叶定律,可得靠近人体皮肤织物的热流、质流密度,对其求积分可得总热通量、总质通量分别为:
(22)
将式(20)、(22)代入式(19)中,可得
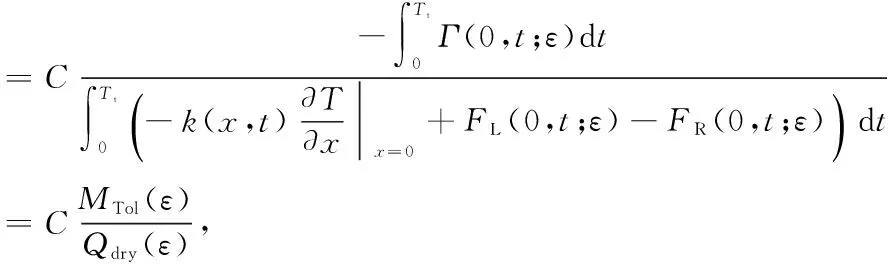

2.2 反问题的数值模拟
下面给出两个反问题数值实例。假定人体皮肤温度为35 ℃,相对湿度为96%;环境温度为-20 ℃,相对湿度为90%。织物的初始温度T0(x)=20 ℃。聚丙烯和纤维胶的参数值见表3。

表3 材质参数值
本文运用遗传优化算法求解最优孔隙率。遗传算法最初由美国Michigan大学J. Holland教授在1975年提出,是一种用来模拟达尔文生物进化论的自然选择和遗传机理的生物进化过程的随机性算法。该方法不依赖于初始值的选择,且在一定条件下,可收敛到优化问题的最优解。
遗传算法计算步骤如下:
a) 随机创建初始种群;
b) 确定每个个体的约束条件和目标函数;
c) 给所有可行解分配适应值,根据适应值来选择父辈;
d) 由父辈产生子辈(交叉和变异);
e) 子辈代替当前种群,类似形成下一辈;
f) 重插子辈,重复b)—f),找到最优个体种群;
g) 满足停止准则,停止算法。
遗传算法的参数定义如下:种群大小或个体数目Nind=50,个体长度Lind=10,变量个数Nvar=1,每个变量用25位的二进制表示,变量的取值范围为[0.5,1.0],最大遗传次数MAXGEN=100,遗传代沟为GGAP=0.9。
为了与遗传算法结果相比较,首先根据目标函数,绘出孔隙率在[0,1.0]区间所对应的透湿指数。选取聚丙烯、纤维胶进行数值模拟,所得结果如图3所示。
由图3可知,无论是选取聚丙烯还是纤维胶,随着孔隙率的不断增大,透湿指数均是先增加后减小。说明在低温条件下,当孔隙率不断增大时,干空气不断增多,阻热值不断增强,织物就越保暖,但当热阻值增大到一定程度时,织物的透气性就会下降。因此,孔隙率为0.784时保暖、透气性最佳。为了得到更高精度的孔隙率,也为了研究多层结构孔隙率决定反问题,本文进一步利用遗传算法进行优化求解,并和图形结果进行比较。
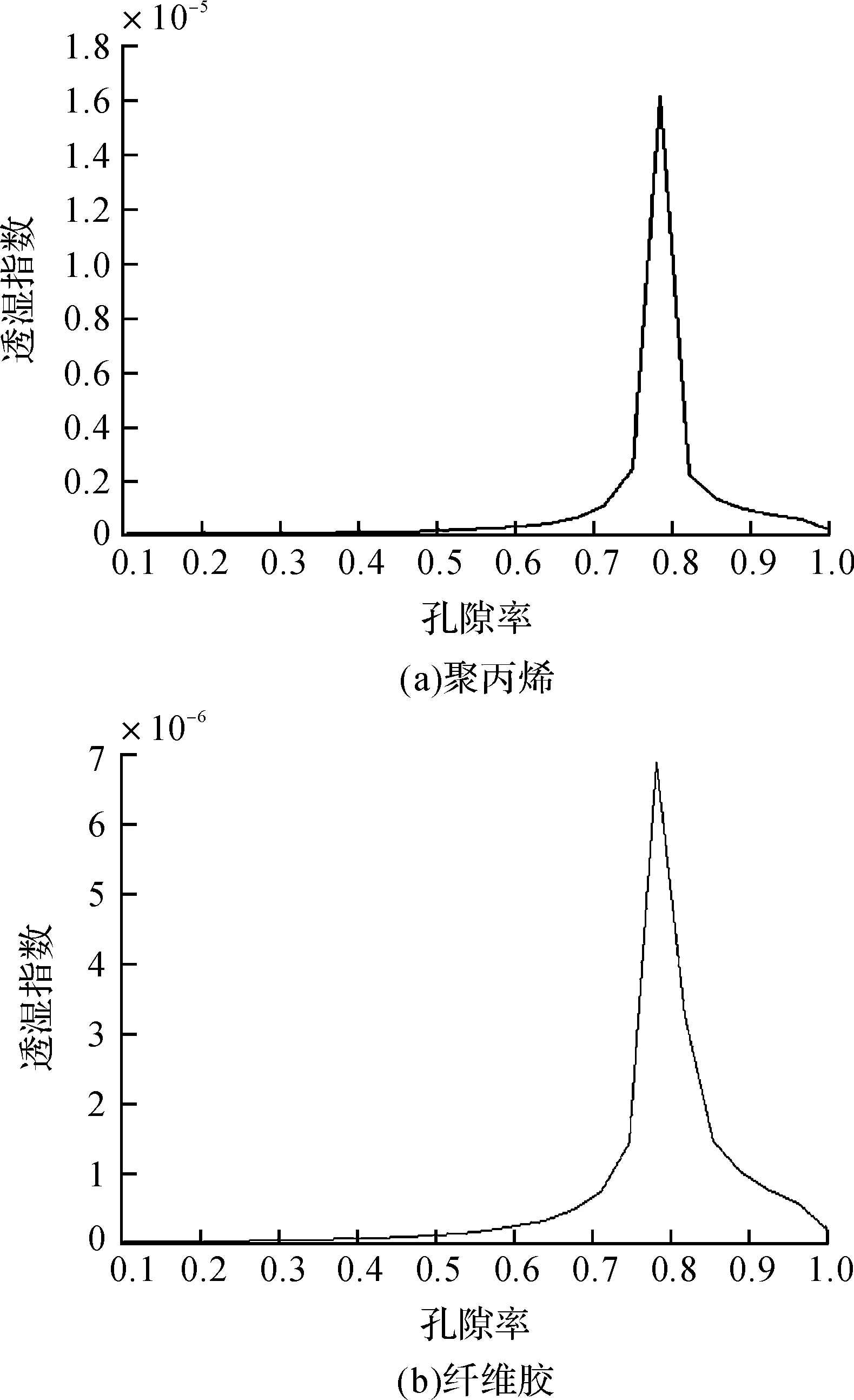
图3 不同材质透湿指数随孔隙率变化的关系

材质图形结果遗传算法误差聚丙烯0.7840.78320.008纤维胶0.7840.79880.015
从表4可看出,两材质孔隙率误差分别为0.008、0.015,数值计算结果与图形结果比较吻合,说明遗传算法的有效性,可将其运用到双层及多层织物结构中。同时也说明,透湿指数这一指标选取的合理性与广泛适用性。
3 结 论
本文给出了一个第三类边界条件的动态热湿传递模型,及其数值解的存在唯一性证明。本文基于该数学模型,以最佳保暖透湿性为目的,根据透湿指数提出了单层织物最优决定孔隙率的反问题,为保暖服的孔隙率取值问题提供了一定的理论依据。热湿舒适性指标是一个静态指标,而透湿指数无论是对静态还是动态情况都适用,因此本文中提出的反问题比采用热湿舒适性指标构造反问题更具适用性。本文只给出单层织物孔隙率决定反问题,可将其推广至双层或多层织物孔隙率组决定反问题,以及热传导、曲折系数等其他参数决定反问题。
[1] Ogniewicz Y, Tien C L. Analysis of condensation in porous insulation[J]. Heat Mass Transfer,1981,24(3):421-429.
[2] Shapiro A P, Motakef S. Unsteady heat and mass transfer with phase change in porous slab: analytical solution and experimental results[J]. Heat Mass Transfer,1990,33(1):163-173.
[3] Murata K. Heat and mass transfer with condensation in a fibrous insulation slab bounded on one side by a cold surface[J]. Heat Mass Transfer,1995,38(17):3253-3262.
[4] Bouddour A, Auriault J L, et al. Heat and mass transfer in wet porous media in presence of evaporation-condensation[J]. Heat Mass Transfer,1998,41(15):2263-2277.
[5] Fan J T, Cheng X Y. Heat and moisture transfer with sorption and phase change through clothing assemblies, part I: experimental investigation[J]. Textile Research Journal,2005,75(2):99-105.
[6] Fan J T, Luo Z X, Li Y. Heat and moisture transfer with sorption and condensation in porous clothing assemblies and numerical simulation[J]. Heat Mass Transfer,2000,43(16):2989-3000.
[7] Fan J T, Wen X H. Modeling heat and moisture transfer through fibrous insulation with phase change and mobile condensates[J]. Heat Mass Transfer,2002,45(19):4045-4055.
[8] Du N, Fan J T, Wu H J. Optimum porosity of fibrous porous materials for thermal insulation[J]. Fibers and Polymers,2008,9(1):27-33.
[9] Du N, Fan J T, et al. Optimum porosity distribution of fibrous insulation[J]. Heat and Mass Transfer,2009,52(19-20):4350-4357.
[10] Korycki R. Method of thickness optimization of textile structures during coupled heat and mass transport[J]. Fibres and Textiles in Eastern Europe,2009,17(1):33-38.
[11] 徐定华,葛美宝,陈瑞林.基于服装舒适性的纺织材料设计反问题[J].应用数学与计算数学学报,2012,26(3):332-341.
[12] Xu D H, Ge M B. Thickness determination in textile material design: dynamic modeling and numerical algorithms[J]. Inverse Problem,2012,28(3):35011-35032.
[13] Xu D H, Chen Y B, et al. Type design for textile materials under low temperature: Modeling, numerical algorithm and simulation[J]. Heat Mass Transfer,2013,60(1):582-590.
[14] Xu Y H, Xu D H, Zhang L P, et al. A new inverse problem for the determination of textile fabrics thickness[J]. Inverse Problems in Science and Engineering,2015,23(4):635-650.
[15] Ye C, Huang H, Fan J T, et al. Numerical study of heat and moisture transfer in textile materials by a finite volume method[J]. Communications in Computational Physics,2008,4(4):929-948.
[16] Havenith G, Heus R, Lotens W. Clothing ventilation, vapor resistance and permeability index: changes due to posture, movement and wind[J]. Ergonomics,1990,33(8):989-1005.
[17] Ding D, Tang T, Song G W, et al. Characterizing the performance of a single-layer fabric system through a heat and mass transfer model: Part I: Heat and mass transfer model[J]. Textile Research Journal,2011,81(9):398-411.

