Monotonicity and convexity properties of the Gamma and Psi functions
,
(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)
0 Introduction

respectively (cf. [1-4]).
During the past decades, many authors have obtained various properties for the functions Γ(x),ψ(x)and its derivatives. (Cf.[3],[5]-[18] and bibliographies there.) For example, in [5, Theorem 1.1 and Lemma 2.1], some inequalities were obtained for the functionf(x)≡xψ(x+1)-log Γ(x+1), and it was proved thatg(x)≡x2[ψ′(x+1)+xψ″(x+1)] is strictly increasing from [0,∞) onto [0,1/2), while the functionx→g(x)/xis not monotone on (0,∞). In [6-7] and [18], several monotonicity properties and inequalities were obtained for the gamma function Γ(x). In [18], it was proved that the functionF(x)≡(x+1)-1[Γ(x+1)]1/x(G(x)≡(x+1)-1/2[Γ(x+1)]1/x) is strictly decreasing (increasing, respectively) on [1,∞). In [7], it was shown that the functionF(G) is strictly decreasing and log-convex(increasing and log-concave, respectively) on (0,∞) by using complicated methods, and some other properties of Γ(x) were derived. Such kind of studies usually rely on analytic properties of Γ(x),ψ(x),ψ(n)(x), and those of certain combinations defined in terms of these functions.
The main purpose of this paper is to improve the above-mentioned known conclusions for the functionsf,g,FandG, and some other main results proved in [7], by applying recent results for Γ(x),ψ(x) andψ(n)(x).
1 Preliminaries
In the sequel, we shall frequently apply the following formulas [1, 6.1.40, 6.4.2 & 6.4.11]:
(1)
ψ(n)(1)=(-1)n+1n!ζ(n+1)
(2)
(3)
whereB2kfork∈Nare the Bernoulli numbers (see [1, 23.1]).
First, we record the following theorem proved in [19, Theorems 1.1-1.2] and needed in the proofs of our results stated in Section 2.
TheoremA. a) For eachn∈N, the functionGn(x)≡(-1)n+1[nψ(n)(x+1)+xψ(n+1)(x+1)] is completely monotonic on [0,∞), withGn(0)=n!nζ(n+1) andGn(∞)=0.
b) Letf1(x)=xGn+1(x)/Gn(x) for eachn∈Nand forx∈[0,∞). Then for eachn∈Nand for allx∈[0,∞),
(4)
c) Forx∈(0,∞), letf2(x)≡x-2(x+1)f(x), wheref(x)=xψ(x+1)-log Γ(x+1). Thenf2is strictly increasing from (0,∞) onto (π2/12,1). In particular,
(5)
for allx∈[0,∞), with equality in each instance if and only ifx=0.

α≤c0<δ
(6)
(7)
and
(8)
forx∈(0,∞). Each of the equalities in (8) holds if and only ifx=0.
Next, we prove the following theorem, which improves [5,Theorem 1.1 & Lemma 2.1].
Theorem1. LetGnandfbe as in Theorem A. For real numbersaandb, define the functionsg1,aandg2,bon (0,∞) by
g1,a(x)=x-af(x) andg2,b(x)=xbG1(x),
respectively. Then we have the following conclusions:
a) The functiong1,ais strictly increasing(decreasing) on (0,∞) if and only ifa≤1(a≥2, respectively), withg1,1((0,∞))=(0,1) andg1,2((0,∞))=(0,π2/12). In particular, forx∈[0,∞),
(9)
with equality in each instance if and only ifx=0.
b) The functiong2,bis strictly increasing (decreasing) on (0,∞) if and only ifb≥2(b≤0, respectively), withg2,2([0,∞))=[0,1/2) andg2,0([0,∞))=(0,π2/6].
Proof: a) Letg1(x)=x2ψ′(x+1)/f(x) forx∈(0,∞). Sincef′(x)=xψ′(x+1)>0,fis strictly increasing on (0,∞) andf(x)>f(0)=0 forx∈(0,∞). By differentiation,
(10)
By [5, Theorem 1.1(4)], we have
(11)
Hence it follows from (10) that
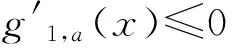
and

This yields the assertion on the monotonicity ofg1,a.
The first inequality and the second upper bound in (9) follow from (5), and the first upper bound in (9) follows from the monotonicity property ofg1,2. The equality case in (9) is clear.
LetG1andf1, withn=1, be as in Theorem A. Then by differentiation,
(12)
which yields the assertion on the monotonicity ofg2,bby Theorem A(2).
2 Some Properties of the Gamma Function
In [7, Theorem 1] ([7, Theorem 2]), it was proved that the function
F(x)≡(x+1)-1[Γ(x+1)]1/x(G(x)≡(x+1)-1/2[Γ(x+1)]1/x)
is strictly decreasing and strictly log-convex(increasing and log-concave, respectively) on (0,∞). Our following theorem improves these known conclusions.
Theorem2. Letc0andαbe as in Theorem A, and for eachc∈R, define the functionFon (0,∞) byF(x)=(x+1)-c[Γ(x+1)]1/x. Then we have the following conclusions:
a)Fis strictly decreasing on (0,∞) if and only ifc≥1, withF((0,∞))=(e-1,e-γ) ifc=1, andF((0,∞))=(0,e-γ) ifc>1. Moreover,Fis log-convex on (0,∞) if and only ifc≥1.
b)Fis strictly increasing on (0,∞) if and only ifc≤π2/12. Ifc≤π2/12, thenF((0,∞))=(e-γ,∞).
c)Fis log-concave on (0,∞) if and only ifc≤c0. In particular,Fis log-concave on (0,∞) ifc≤α.
Proof: Letg1,2,f2andf3be as in Theorem 1, Theorem A(c) and Theorem A(d), respectively. Then by differentiation, we obtain
(13)
(14)
(15)
a) By (14) and Theorem A(3), forx∈(0,∞),
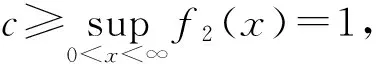
which shows thatFis strictly decreasing on (0,∞) if and only ifc≥1.
It follows from (7) and (13) that

It is well know thatψ(1)=-γ(see [1, 6.3.2]). Ifc=1, then by l’Hpital’s rule and (1),

Similarly, ifc>1, thenF(0+)=e-γand
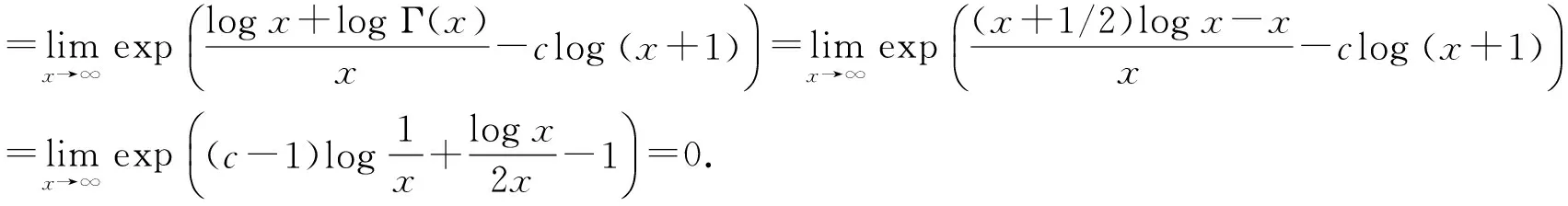
b) It follows from (14) and Theorem A(3) that for allx∈(0,∞),

that is,Fis strictly increasing on (0,∞) if and only ifc≤π2/12.
Clearly, ifc≤π2/12, thenF(0+)=e-γ. SinceF(∞)=e-1whenc=1,
c) It follows from (13), (15) and Theorem A(d) that on (0,∞),

The remaining conclusion is clear.
The following corollary improves [7, Corollaries 1-2].
Corollary3. Forx,y∈(0,∞) withy≥x,
(16)
with equality in each instance if and only ify=x. Moreover, forx∈(0,∞),
h2(x)x<Γ(x+1)<[e-γ(x+1)]x
(17)
whereh2(x)=max{e-1(x+1), e-γ(x+1)π2/12}.
Proof: It follows from Theorem 2(a)-(b) that
with equality in each instance if and only ify=x. This yields the double inequality (16) and its equality case.
The double inequality (17) follows from Theorem 2(a)-(b).
Remark. Leth2be as in Corollary 3, andh3(x)=eγ-1(x+1)1-π2/12forx∈(0,∞). Then it is clear thath3is strictly increasing from (0,∞) onto (eγ-1,∞), and
e-1(x+1)/[e-γ(x+1)π2/12]=h3(x).
Hence there exists a unique numberx1∈(0,∞) such that the function
In [7, Theorems 4-5], it was proved that the functionG(x)≡Γ(x+1)1/xis strictly increasing on (0,∞), andH(x)≡xηΓ(x+1)1/xis strictly increasing (decreasing) on (0,∞) ifη≥0(η≤-1, respectively). The following theorem strengthens these results.
Theorem4. a) The functionG(x)≡Γ(x+1)1/xis strictly increasing and log-concave from (0,∞) onto (e-γ,∞).
b) For eachη∈R, define the functionHon (0,∞) byH(x)≡xηΓ(x+1)1/x. ThenHis strictly increasing(decreasing) on (0,∞) if and only ifη≥0(η≤-1, respectively), withH((0,∞))=(e-γ,∞) ifη=0, andH((0,∞))=(1/e,∞) ifη=-1.
Proof: a) By logarithmic differentiation,G′(x)/G(x)=g1,2(x), whereg1,2is as in Theorem 1. This yields the monotonicity and log-concavity properties ofGby Theorem 1(a).
Clearly,G(0+)=e-γ. Applying (1), we can obtain the limiting valueG(∞)=∞.
b) Letg1,1be as in Theorem 1. Then by logarithmic differentiation,xH′(x)/H(x)=η+g1,1(x), and hence the assertion on the monotonicity ofHfollows from Theorem 1(a).
It is clear thatH(x)=G(x) ifη=0. HenceH((0,∞))=(e-γ,∞) ifη=0.
Ifη=-1, thenH(x)=G(x)/x, so thatH(0+)=∞. By (1.1),H(∞)=e-1.
[1] Abramowitz M, Stegun I A. Handbook of Mathematical Functions With Formulas, Graphs and Mathematical Tables[M]. New York: Dover,1965.
[2] Andrews G, Askey R, Roy R. Special Functions, Encyclopedia of Mathematics and Its Applications[M]. Cambridge: Cambridge Univ Press,1999.
[3] Anderson G D, Vamanamurthy M K, Vuorinen M. Conformal Invariants, Inequalities, and Quasiconformal Mappings[M]. New York: John Wiley & Sons,1997.
[4] Qiu S L, Vuorinen M. Handbook of Complex Analysis: Special Function in Geometric Function Theory, Volume 2[M]. Elsevier B V,2005:621-659.
[5] Qiu S L, Zhao X. Some properties of the psi function and evaluations ofγ[J]. Appl Math J Chinese Univ Ser B,2016,31(1):103-111.
[6] Qi F. Bounds for the ratio of two gamma functions[J/OL]. J Ineq Appl, 2010: 1-84. http://doi:10.1155/2010/493058.
[7] Qi F, Chen C P. Monotonicity and convexity results for functions involving the gamma function[J]. Periodica Mathematica Hungarica,2003,65(1):27-36.
[8] Alzer H. On Ramanujan’s double inequality for the gamma function[J]. Bull London Math Soc,2003,35(5):601-607.
[9] Alzer H. Gamma function inequalities[J]. Numer Algor,2008,49(1):53-84.
[10] Aderson G D, Qiu S L. A monotoneity property of the Gamma function[J]. Proc Amer Math Soc,1997,125(11):3355-3362.
[11] Batir N. On some properties of the gamma function[J]. Expo Math,2008,26(2):187-196.
[12] Batir N. Inequalities for the gamma function[J]. Arch der Mathematik,2008,91(6):554-563.
[13] Elbert A, Laforgia A. On some properties of the gamma function[J]. Proc Amer Math Soc,2000,128(9):2667-2673.
[14] Mortici C. Further improvements of some double inequalities for bounding the gamma function[J]. Math Comput Modelling,2013,57(5/6):1360-1363.
[15] Mortici C. Sharp bounds for gamma function in terms ofxx-1[J]. Appl Math Comput,2014,249:278-285.
[16] Qi F. Refinements of lower bounds for polygamma functions[J]. Proc Amer Math Soc,2013,141(3):1007-1015.
[17] Qiu S L, Vuorinen M. Some properties of the gamma and psi functions with applications[J]. Math Comput,2005,74(250):723-742.
[18] Chen C P, Qi F. Monotonicity results for the gamma function[J/OL]. J Ineq Pure Appl Math,2003,4(2). http://http://www.emis.de/journals/JIPAM/images/065_02_JIPAM/065_02.pdf.
[19] Qiu S L, Ma X Y, Huang T R. Monotonicity and convexity Theorems for the nth-derivatives of the psi function with applications[J]. (Manuscript submitted.)

