一道中考压轴题的来龙去脉

☉江苏省南通市通州区平潮实验初中 丛远林

一、题目来源

题目：（2018年江苏·南通卷第28题第（3）问）【定义】如图1，A、B为直线l同侧的两点，过点A作点A关于直线l的对称点A′，连接A′B交直线l于点P，连接AP，则称点P为点A、B关于直线l的“等角点”.

图1

图2

题目中的新定义来源于人教版八年级上册“13.4课题学习 最短路径问题”问题1的解答，由于∠APM=∠BPH，给出了“等角点”的新定义.

将等边三角形外接圆中一个简单结论放到新定义背景下.作等边三角形ABC的外接圆O′（如图3），点P在弧ACB上（不与点A、B重合）.当点P不与点C重合时，作直线CP，发现始终有∠APC=∠BPD，所以在等角点新定义背景下，图3中任何一条直线CP，点P就成了点A、B关于直线CP的等角点，也就是说任何一条直线CP，都成为定义中的直线l.当点P与点C重合时，过点C作圆的切线，点C是点A、B关于这条切线的等角点，这条切线是定义中的直线l.图3中定义中的直线l都过点C，图3中直线l的临界线是直线CA、CB.

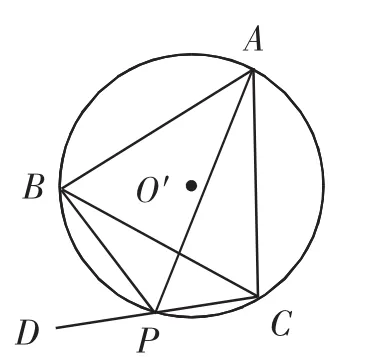
图3

将图3放入平面直角坐标系中，与一次函数结合，如图4，直线y=ax+b都过点C，直线y=ax+b的临界线是直线CA、CB.又a≠0，所以平行于x轴的直线CS不合题意，所以临界线是直线CA、CB、CS.求出这三条直线解析式中的b，就知道了b的取值范围.

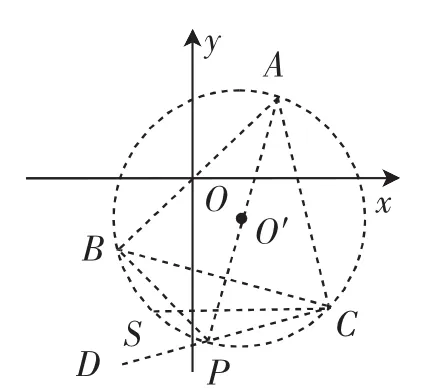
图4

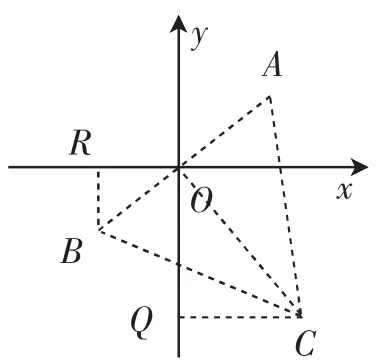
图5

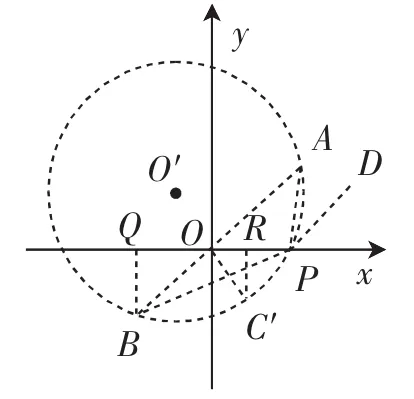
图6

二、题目再创造

1.类比

（1）当∠APB=120°时，其他条件不变，求b的取值范围.

分析：如图6，作过点A、B的圆O′，O′在直线AB的左上方，使∠AO′B=120°，则点P在弧AB上（不与点A、B重合）.点C′为弧AB的中点，当点P不与点C′重合时，作直线C′P，则始终有∠APD=∠BPC′，点P都是点A、B关于直线C′P的等角点.当点P与点C′重合时，过点C′作圆的切线，点C′是点A、B关于这条切线的等角点，定义中的直线l都过点C′.直线y=ax+b的临界线是直线C′A、C′B，求出这两条直线解析式中的b，就知道了b的取值范围.

在Rt△AOC′中，∠AOC′=90°，∠AC′O=60°，OA=.构造Rt△C′RO Rt△OQB，求出求出直线C′A中，直线C′B中，所

∠APB换成钝角，结论形式发生了变化.

（2）当点P位于直线AB的左上方，∠APB=45°时，其他条件不变，求b的取值范围.

分析：如图7，作过点A、B的圆O′，O′在直线AB的左上方，使∠AO′B=90°，则点P在弧ACB上（不与点A、B重合）.点C为弧ACB的中点，直线y=ax+b的临界线是直线CA、CB、CR，求出这三条直线的解析式中的b，就知道了b的取值范围.

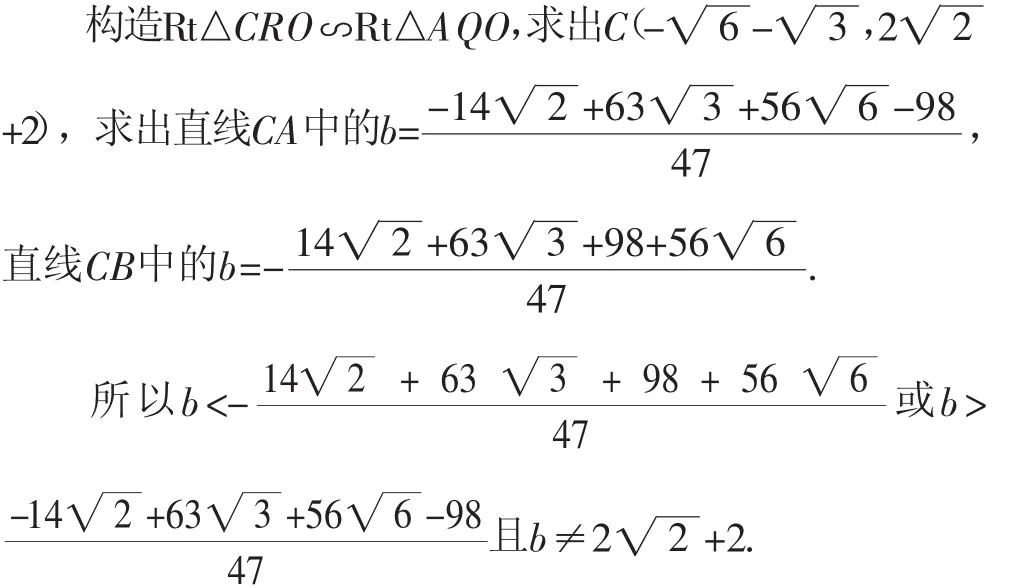
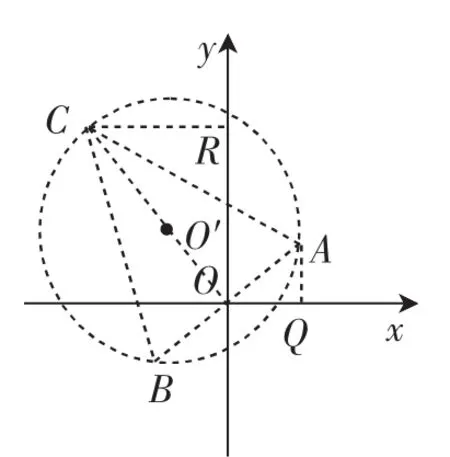
图7

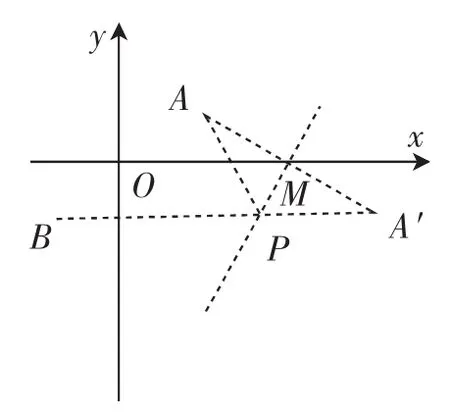
图8

2.互换题设和结论

分析：作点A关于直线y=x-5的对称点A′（如图8）.由于AA′⊥PM，可求出直线AA′的解析式中的，从而求出直线AA′的解析式.联立方程，求出点M（5，0），所以A（′8，-），求出直线A′B的解析式y=-，求出点P（4，-），用两点之间距离公式求出AM、AP的长，

解Rt△AMP，求出∠APM=60°，所以∠APB=60°.

分析：α为定值，90°＜α＜180°，如图6，直线y=ax+b的临界线是直线C′A、C′B. 又所以直线C′A中的，直线C′B中的从而求出直线C′A、C′B的解析式.联立方程，求出点.解Rt△AOC′，求出∠AC′O=60°，从而α=120°.

3.拓展

等边三角形外接圆中结论可拓展为一般情形.如图9，点C是弦AB所对弧的中点，点P在弧ACB上（不与点A、B重合）.当点P不与点C重合时，作直线CP，发现始终有∠APC=∠BPD.当点P与点C重合时，过点C作圆的切线MN，有∠ACM=∠BCN.

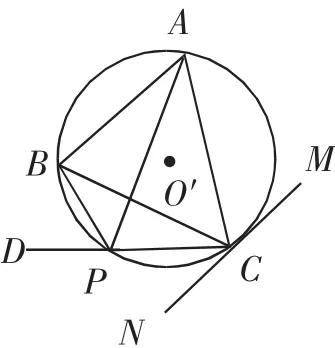
图9

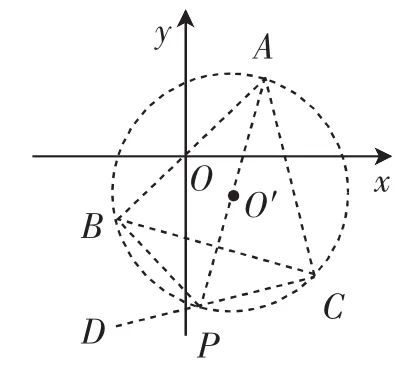
图10

分析：当点P在直线AB的右下方时.

如图10，作过点A、B的圆O′，使∠AO′B=2α，点C为弦AB所对优弧的中点，则点P在弧ACB上（不与点A、B重合）.当点P不与点C重合时，作直线CP，则始终有∠APC=∠BPD，点P是点A、B关于直线CP的等角点.当点P与点C重合时，过点C作圆的切线，点C是点A、B关于这条切线的等角点，定义中的直线l都过点C.直线y=ax+b的临界线是直线CA、CB、CS（如图11），求出这三条直线的解析式中的b，就知道了b的取值范围.

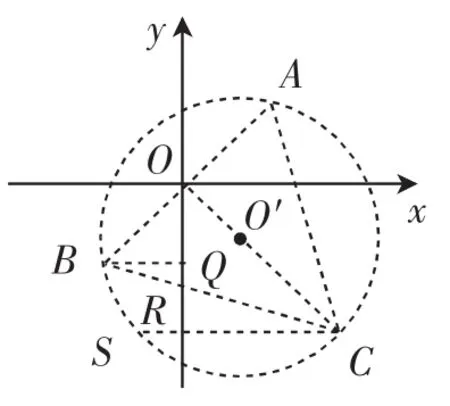
图11

图12

当点P在直线AB的左上方时.

分析：当点P在直线AB的右下方时.

如图13，作过点A、B的圆O′，使∠AO′B=360°-2α，点C为弦AB所对劣弧的中点，则点P在弧ACB上（不与点A、B重合）.直线y=ax+b的临界线是直线CA、CB，求出这两条直线解析式中的b，就知道了b的取值范围.

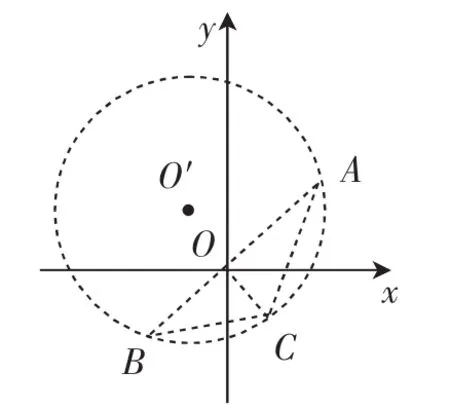
图13

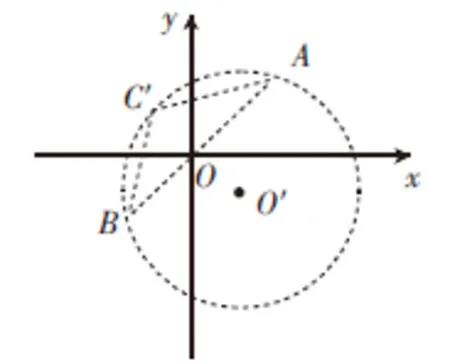
图14

当点P在直线AB的左上方时.