一道中考压轴题的多种解法与教学思考

☉山东省水发实验学校 刘增元

综合运用函数、图形变换、求最值等知识的动点问题成为近几年中考压轴题的热点题型，备受一线教师的关注.下面以菏泽市2018年中考压轴题（第24题）为例，提供多种解法，并跟进教学思考，分享给大家.

一、试题呈现与解析

如图1，在平面直角坐标系中，抛物线y=ax2＋bx-5交y轴于点A，交x轴于点B（-5，0）和点C（1，0），过点A作AD∥x轴交抛物线于点D.

（1）求此抛物线的表达式；

（2）点E是抛物线上一点，且点E关于x轴的对称点在直线AD上，求△EAD的面积；

（3）若点P是直线AB下方的抛物线上一动点，当点P运动到某一位置时，△ABP的面积最大，求出此时点P的坐标和△ABP的最大面积.

图1

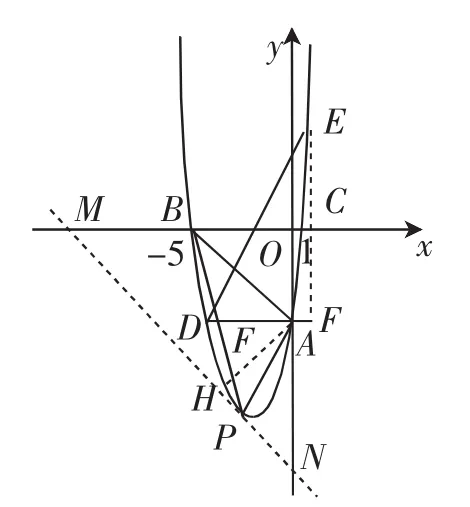
图2

思路分析：（1）将B、C两点的坐标分别代入抛物线y=ax2＋bx-5，用待定系数法可求出抛物线的表达式.

（2）求△EAD的面积，必须确定其底和高.因为线段AD的长度可求，且平行于x轴，可作为底，然后根据点A的坐标和轴对称求出AD边上的高，进而求出△EAD的面积.

（3）求△ABP的最大面积，基本方法有两种.一种是几何法.由题意可知线段AB的长度一定，所以求出动点P到直线AB的最大距离，就能求出△ABP的最大面积.当把直线AB向下平移，和抛物线有一个公共点P时，点P到直线AB的距离达到最大，此时可求出点P的坐标和△ABP的最大面积.另一种是解析法.设出点P的坐标，利用面积割补转化法，即把不可直接求（或表示）的三角形面积转化为可求（或可表示）的面积的和、差，然后借助函数求最值.

解：（1）抛物线y=ax2＋bx-5过点B（-5，0）、C（1，0），则解得a=1，b=4.

所以抛物线的表达式为y=x2＋4x-5.

（2）当x=0时，y=x2＋4x-5=-5，则A（0，-5）.

因为点E关于x轴的对称点F在直线AD上，且AD∥x轴，所以EF⊥DA，EF=10.

由x2＋4x-5=-5，解得x1=-4，x2=0，则AD=x2-x1=4，故S△EAD=×4×10=20.

（3）（几何法）如图2，设直线AB的表达式为y=kx＋b.

所以直线AB的表达式为y=-x-5.

过抛物线上的点P作直线MN∥AB分别交x、y轴于点M、N.设直线MN的表达为y=-x＋b.

由x2＋4x-5=-x+b，得x2+5x-5-b=0.当直线y=-x+b与抛物线y=x2＋4x-5只有一个公共点时，Δ=25-4（-5-b）=0，则b=-，点P的横坐标为-，纵坐标为-，所以点直线MN的表达式为y=-，它与y轴交

作AH⊥MN，垂足为H.

因为OA=OB=5，则∠BAO=45°，∠MNA=45°.

注：求△ABP边AB上的高，也可过点O作平行线AB与MN的垂线，利用垂线段的差来求，限于篇幅，这里不再赘述.

试题点评：本题作为压轴题有以下特点.

（1）题干字符简洁，问题梯度分明，由易到难，由静到动，思维水平逐级提高，使不同水平的学生到达问题的不同深度，体现了新课标的基本理念“面向全体学生”“不同的人在数学上得到不同的发展”.

（2）以函数为主脉，由简单到复杂，涵盖了待定系数法、图形变换、图形与坐标、配方法、数形结合、化归、函数与方程和函数建模等主要数学思想方法的考查，实现了函数与几何的有机结合.

（3）问题前后关联，解法多样，通性、通法与技巧相结合，探究持续进行.问题（1）是问题（2）和（3）的解题基础，问题（2）和（3）看似没有关联，但实质上问题（2）是为问题（3）做铺垫，问题（3）在试题解析中用了几何法，还可以用解析法，即在平面直角坐标系中，学生可以结合自己的解题经验从不同角度将△ABP的面积割补转化，然后利用函数求出△ABP的最大面积.解法多样，丰富多彩，这些正体现了命题者的匠心.

二、本题第（3）小题解析法赏析

解法1：如图3，过点P作PE⊥OB，PG⊥AB，垂足分别为E、G，PE交AB于点F.

由几何解法可知直线AB的表达式为y=-x-5.

设点P（m，m2＋4m-5），则点F（m，-m-5）、E（m，0）.

故PF=（-m-5）-（m2＋4m-5）=-m2-5m.

因为OA=OB=5，PE∥OA，所以∠PFA=∠BAO=45°.

解法2：如图3，过点P作PE⊥OB，垂足为E，交AB于点F.

设点P（m，m2+4m-5），由解法1可知：PF=-m2-5m.

图3

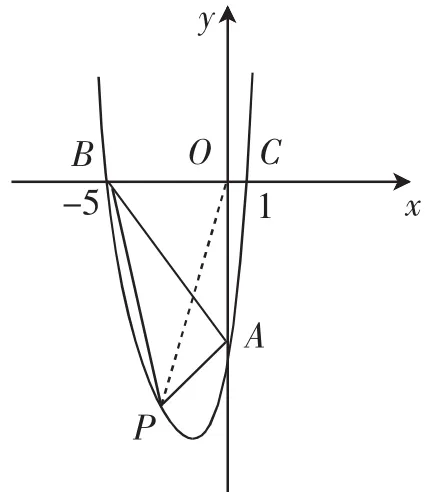
图4

解法3：如图4，连接OP.

设点P（m，m2+4m-5）.

解法4：如图5，作PE⊥OB，垂足为点E.

设点P（m，m2+4m-5）.

图5

图6

解法5：如图6，作PQ⊥y轴，垂足为点Q.

设点P（m，m2+4m-5）.

解法6：利用点到直线的距离公式求解.

先求出直线AB的表达式为y=-x-5.

设点P（m，m2+4m-5）.

因为-5＜m＜0，所以m2+5m＜0.点P到直线AB的距离d=

△ABP

三、教学思考

1.注重数学思想方法在数学教学中的渗透

数学思想方法是数学的灵魂，只有掌握了数学思想方法，才能体会到数学的奥妙，领会数学的精髓，因此教师在数学教学中不仅仅是让学生学会知识，还要着重培养学生的思维能力，把数学思想方法的渗透和数学活动经验的积累贯穿于教学全过程，使学生在学习基础知识的同时掌握数学思想方法，并通过不断积累运用，内化为自己的知识经验，让学生在遇到“陌生”的问题时，会用数学思想方法和自己的经验解决问题.

2.重视解题反思，勤于归纳、梳理

对于数学试题中的压轴题，不能仅仅满足于解出答案这一最低层次，更要善于解后反思.首先，要深入思考试题的结构特点，解法如何自然生成，与以前哪些试题结构类似，解题思想方法是否相同，并对反思进行归纳、梳理，研究解决一类问题的通性通法，以达到对一类问题的深刻理解.其次，要挖掘试题的潜在功能和作用，进行一题多解、一题多变、多题归一，在变式教学中培养学生思维的灵活性和发散性，逐步提升解决问题的能力.