一种改进的机械臂逆运动学阻尼最小二乘算法*
王云鹏,解永春,2,3
0 引 言
运动学是机器人学中重要的基础组成部分.运动学又分为正运动学和逆运动学,其中正运动学研究的是机械臂关节运动特性到机械臂末端运动特性的关系,而逆运动学反之.正运动学相对简单,经过简单的计算就可以计算出相应关系,但逆运动学相对较为复杂,往往是超越方程的形式. 本文重点研究了机械臂的逆运动学求解问题.逆运动学可以将机械臂末端工作空间的控制问题转换到关节空间,从而降低控制难度.因此研究机械臂的逆运动学求解问题具有重要意义.
常见的机械臂逆运动学求解方法包括:解析法、几何法和数值迭代法[1]. 对于复杂的机械臂系统,解析法和几何法的求解难度非常大. 而数值法具有计算简单的优势,不论多么复杂的机械臂都可以对其逆运动学进行求解. 常见的数值求解法包括[2]:循环坐标下降法等[3-5],雅克比伪逆法[6-7]、雅克比转置法[8-9]、奇异值分解法、阻尼最小二乘法[10-11]、雅克比伪逆阻尼最小二乘法、选择性阻尼最小二乘法[12]、反馈逆运动学法[13]、牛顿法[14-15]、连续蒙特卡洛法[16]等.其中循环坐标下降法是一种迭代启发式算法,如果机械臂的自由度为N,那么每次迭代要计算搜索N次,每次只更新一个关节角.循环坐标下降算法具有简单、对初值不敏感、全局性好的特点,但该算法在初值远离理想值的时候收敛速度快,但当接近理想值的时候收敛速度会大幅下降[17].为了解决这个问,文献[3]给出了一种循环坐标下降与BFS联合法,首先利用循环坐标下降法搜索近似解,然后再利用BFS法搜索精确解.雅克比伪逆法、雅克比转置法、阻尼最小二乘、雅克比伪逆阻尼最小二乘法和选择性阻尼最小二乘法都隶属于迭代的雅可比法.雅克比伪逆阻尼最小二乘法和选择性阻尼最小二乘法是阻尼最小二乘法的改进.阻尼最小二乘法性能表现依赖于阻尼系数λ的选取,只有适当的阻尼系数才能保证算法收敛.
上述大部分文献对机械臂的关节角没有任何约束限制,但实际机械臂的关节角都应该有范围限制.文献[7]采用梯度投影法来处理机械臂关节角限位问题.文献[18]给出了一种加权最小二乘法来处理关节角限位问题.文献[19]给出了一种利用关节冗余避免关节限位的方法.此外,基于阻尼最小二乘法,文献[20]提出了一种可以处理关节约束的改进的阻尼最小二乘法.该方法可以一定程度上处理关节限位的问题,但并不能保证关节角不会超过其允许范围.
本文给出了一种求解机械臂逆运动学的改进阻尼最小二乘算法.该算法不依赖于阻尼系数的选取,能保证算法的稳定性和收敛性.此外本文还研究了机械臂的关节约束问题,可以保证机械臂关节角不超出关节允许范围.
1 问题描述
考虑如图1所示的由L(L>0)个连杆组成的串联机械臂,假设所有关节都为转动关节. 机械臂末端理想位姿由理想系表示. 机械臂逆运动学要解决的问题是找出一组关节角使机械臂末端达到理想位姿,即末端系与理想系重合.
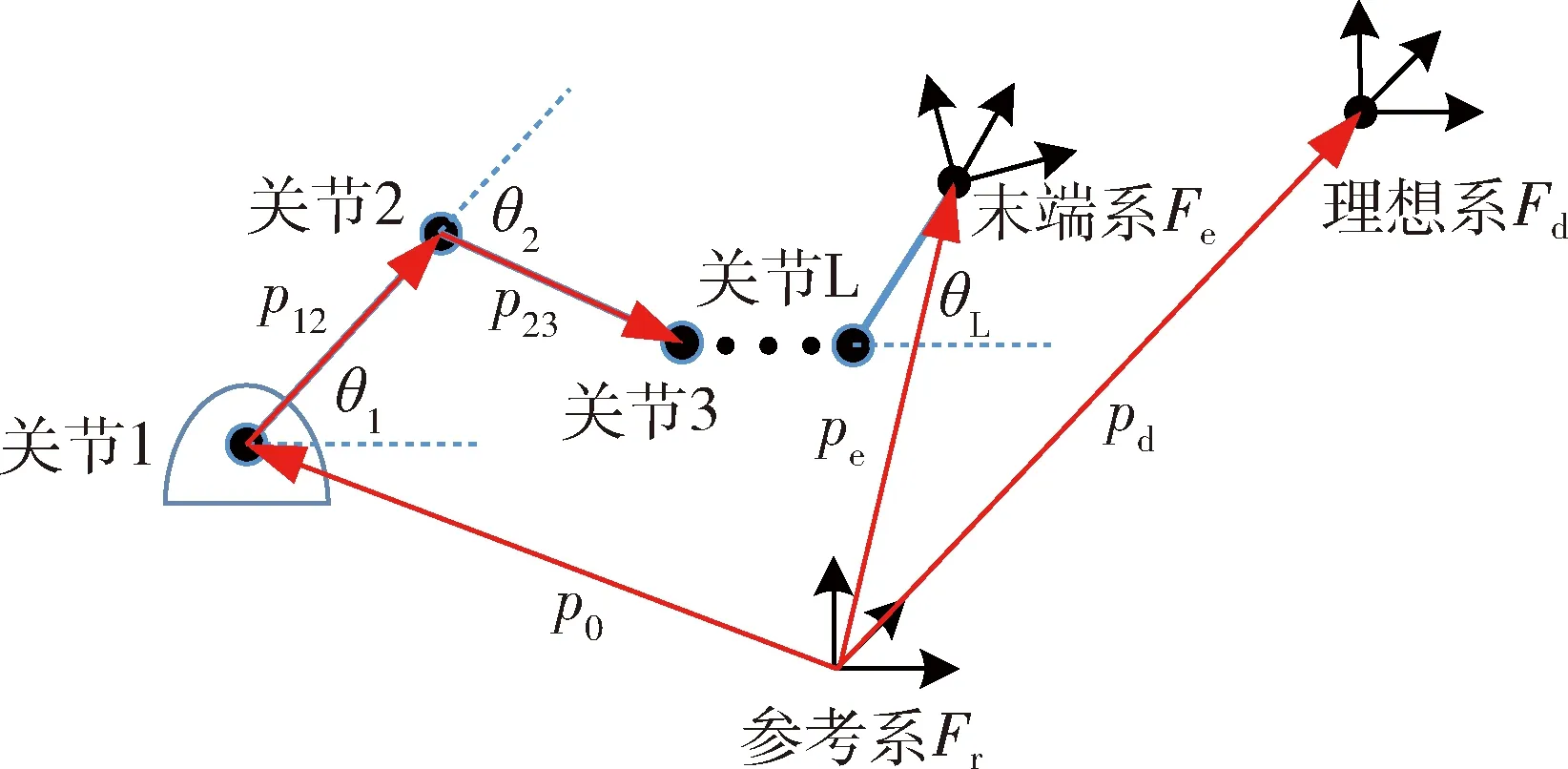
图1 多连杆机械臂Fig.1 Multi-link manipulator
2 问题建模
利用机械臂的几何参数,可以计算出当前关节角θ=(θ1,…,θL)下,机械臂末端的位置为
pe=Fp(θ)∈R3,
末端姿态为
qe=Fq(θ)∈R4,或re=Fr(θ)∈R3,
其中qe和re分别为末端姿态四元数向量和修正的罗德里格斯参数. 姿态四元数的定义参见[21],修正罗德里格斯参数参见文献[22].
给定末端理想位置为pd,末端理想姿态为qd或rd,那么末端位姿和理想位姿的差分别为:
其中姿态差对应的修正罗德里格斯参数为Δre.机械臂的逆运动学求解问题的本质就是寻找一组关节角θ=(θ1,…,θL),使末端位姿误差向量Δpe和Δre都为零.
定义末端位姿误差函数如下
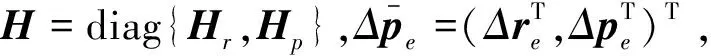
注1.文献[17]对于某些实际应用,并不要求机械臂末端严格跟踪某一位姿曲线. 比如在基于机械臂的弧焊操作中,要求机械臂末端沿着理想位置轨迹运动,而姿态只要求末端结构与弧焊表面垂直即可文献[17]. 也就是说三轴姿态中只要其中一轴跟踪理想轨迹即可. 如果此轴为轴,那么为了解决这个问题,只要将Hr设置为Hr=diag{hr,0,0},其中hr>0.
3 逆运动学求解
3.1 经典阻尼二乘法
首先简单回顾经典阻尼最小二乘算法. 阻尼最小二乘方法是雅克比伪逆法的一种改进方法,因此首先简单介绍雅克比伪逆法[23-24],雅可比伪逆法是一种数值迭代法,该方法的每一步迭代都按照如下的公式计算关节角更新.
θ=θ+Δθ=θ+J†Δp,
其中J†为雅克比矩阵J的一种伪逆,Δp为末端误差. 但当雅可比矩阵接近行不满秩时,伪逆元素的值往往较大,从而很可能导更新角度Δθ过大,致使算法发散. 因此,雅可比伪逆法在雅克比接近行不满秩时,很容易出现不稳定的情况[24-25]. 为了解决这个问题,学者提出了的阻尼最小二乘方法,该方法的每一步关节更新为
Δθ=(JTJ+λ2E)-1JTΔp.
相较于雅可比伪逆法,阻尼最小二乘方法引入了阻尼系数. 当雅可比矩阵距行不满秩点较远的时候阻尼系数设为,此时计算的关节更新向量与雅可比伪逆法相同. 当雅可比矩阵接近行不满秩时,取阻尼系数,大于零的阻尼系数可以使更新步长不至于过大从而提高算法稳定性.
阻尼最小二乘算法表现的好坏依赖于阻尼系数的选取,只有选取适当的阻尼系数,才能保证误差函数快速稳定的收敛. 以往关于阻尼最小二乘的算法研究大多集中在阻尼系数的选取上.
3.2 改进的阻尼二乘法
本节从最优化问题的角度出发,给出一种改进的阻尼最小二乘法. 首先引入下降方向的概念如下,
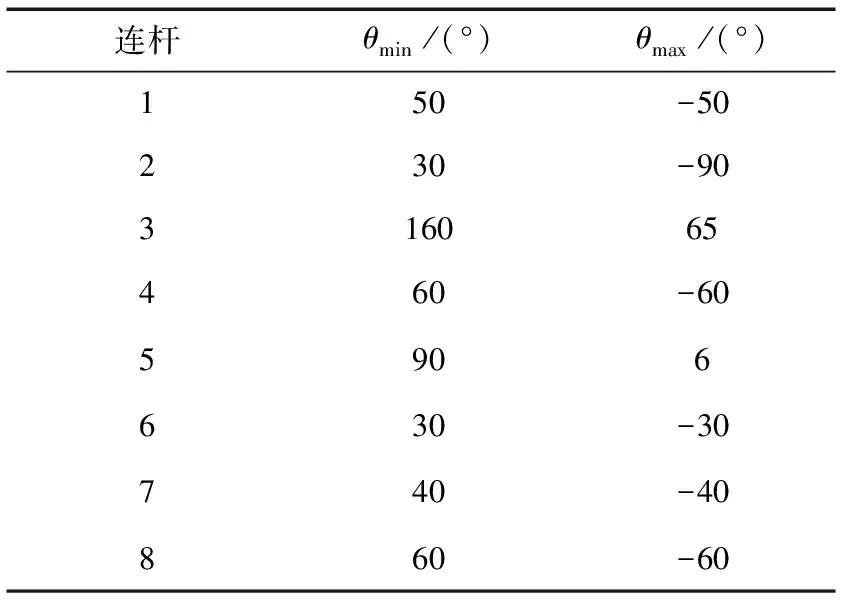
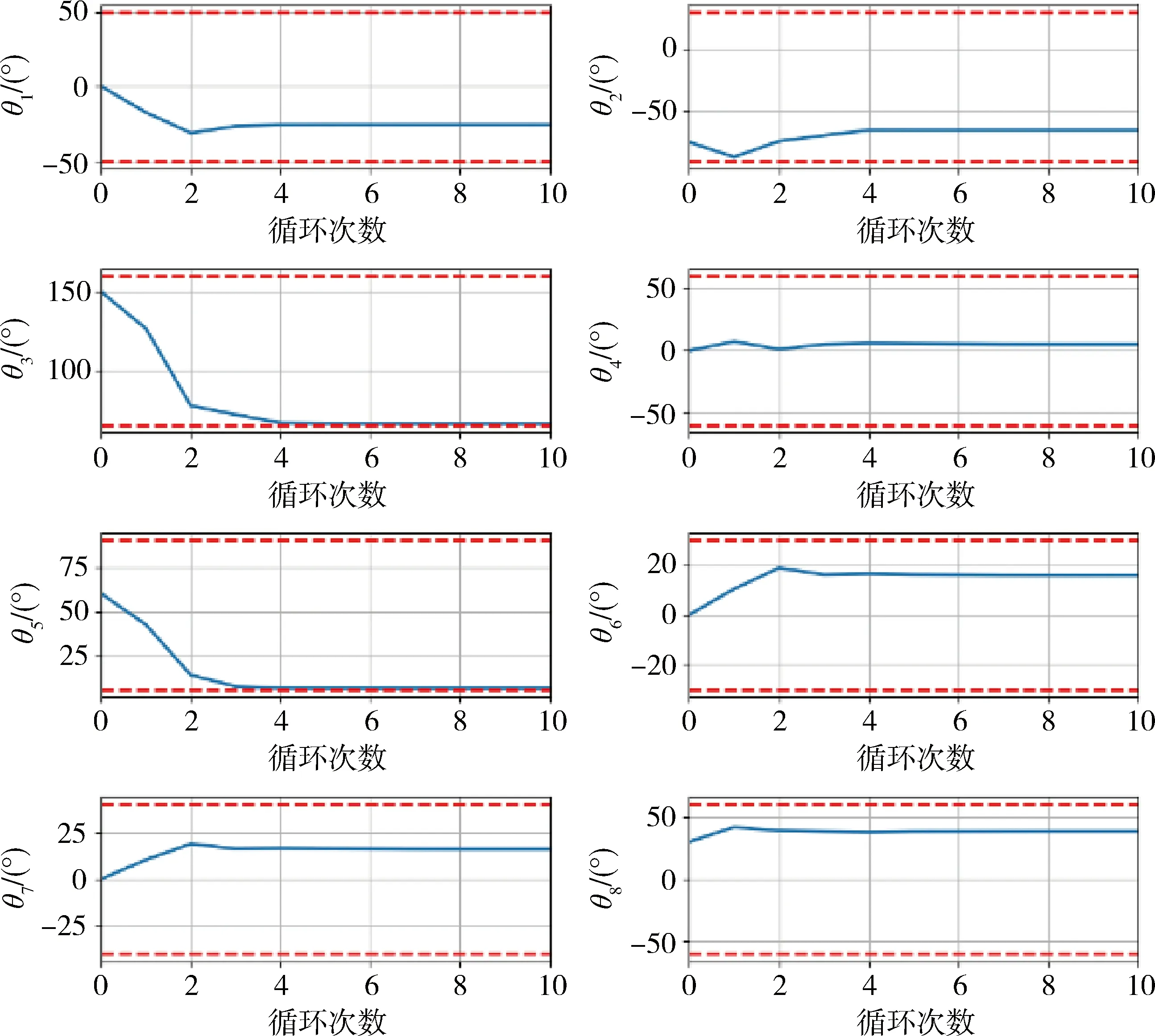
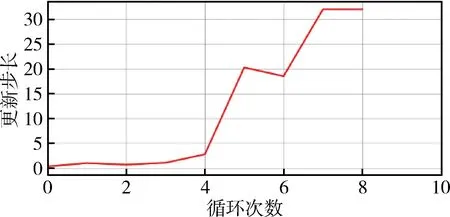
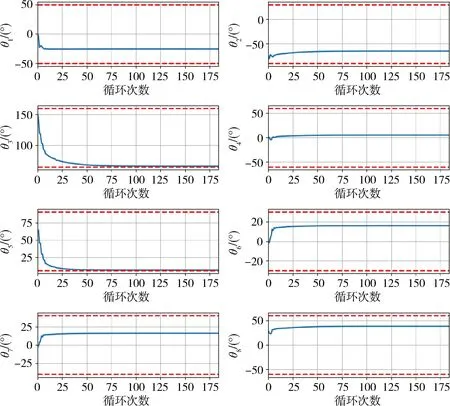
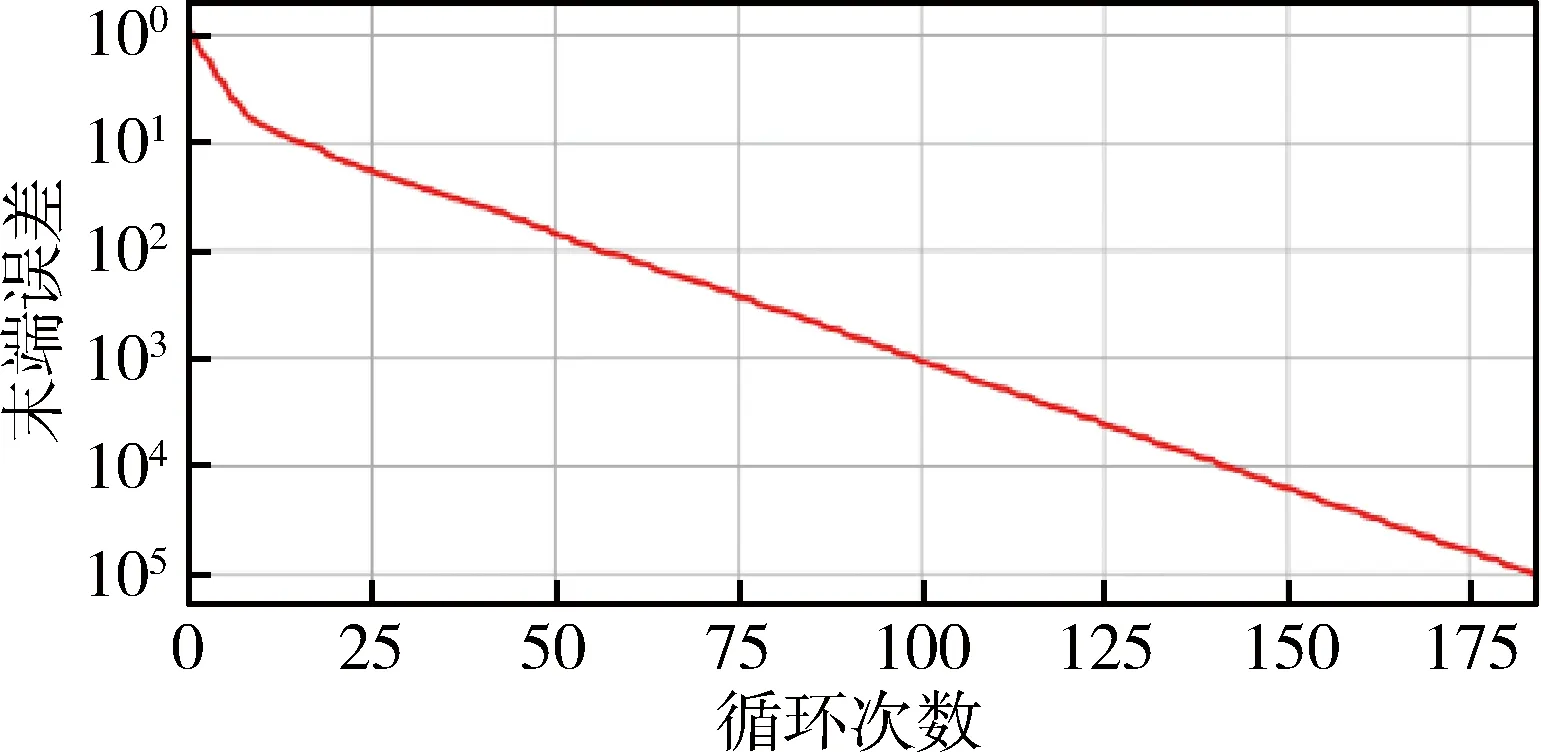
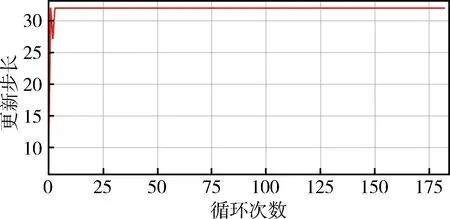
定义1[27].对于函数f(x):Rn→R和向量xd,如果存在δ>0使得f(x+xdt) 机械臂逆运动学求解问题就等价于如下的最优化问题 上述最优化问题可以通过如下的思路解决 1)寻找Err(θ)在θ处的下降方向dθ; 2)寻找适当更新步长dT,使得 Err(θ+dθdT) 3)更新关节角θ=θ+dθdT; 4)重复以上步骤直到误差足够小或达到最大循环次数. 经典阻尼最小二乘法可以看作是上述思路的一个特例,经典阻尼最小二乘法对应的下降方向和更新步长分别为Δθ=(JTJ+λ2E)-1JTΔp和dT=1. 上面的思路的关键为下降方向和更新步长的选取,下面两节将分别给出相应的计算方法. 基于上述思路,采用下面两节提出的下降方法和更新步长计算方法,就得到了一种改进的阻尼二乘算法. 3.2.1 下降方向 由文献[28]可知,机械臂关节速度和末端速度具有如下的关系 引理1. 如果机械臂末端角速度和线速度分别如下 那么一定存在δ使得∀t∈(0,δ), 证明. 计算可得 显然一定存在常数δ>0,使得∀t∈(0,δ) 当雅可比矩阵J行满秩时,那么矩阵JJT为非奇异矩阵. 由文献[26]可知上述最小二乘问题的解为 (1) 其中阻尼系数设计如下 (2) 其中εJ>0,λc>0. 问题(1)等价于 由于[JT,λEL]T行满秩,由[26]可知上述最小二乘问题的解为 (3) 注2.[10]雅可比矩阵J可以SVD分解为J=UΣV,其中U∈→R6×6和V∈RL×L是两个正交矩阵,Σ=[D,06×(L-6)],D=diag{d1,…,d6}∈6×6.计算可得 (JTJ+λEL)-1JT =(VTΣTUTUΣV+λEL)-1VTΣTUT =VT(ΣTΣ+λEL)-1ΣTUT 显然D(D2+λE6)-1=(D2+λE6)-1D,因此有(JTJ+λEL)-1JT=JT(JJT+λE6)-1.因此式(3)等价于 (4) 显然当雅可比矩阵列数大于行数时,式(4)比(3)具有更高的计算效率. 证明. 计算可得 因此一定存在常数δ>0,使得∀t∈(0,δ), 3.2.2 更新步长 上述最优问题可以通过精确搜索方法求解,但精确搜索方法需要消耗大量的计算资源,为此采用Armijo非精确搜索方法[27],设计如下的步长非精确搜索算法. 算法1.步长非精确搜索算法Algorithm 1. Inexact search for the step length 定理1和算法 1可以保证了改进的阻尼最小二乘算法的收敛性. 3.2.3 收敛速度 本节将对改进阻尼二乘算法的收敛速度进行分析. 从以上分析可以看出,大的阻尼常数会导致收敛速度变慢,但并非阻尼常数越小越好.因为过小的阻尼常数很可能会导致算法1迭代次数过多,从而导致收敛速度变慢.因此虽然无论阻尼常数如何选择,改进的算法都会收敛.但不宜选择过大或过小的阻尼常数.第5章将给出两个算例,验证以上结论. 前面两节中都没有考虑关节约束的问题,但是实际机械臂的关节一般不能360度无限制旋转,有限定的允许范围. 本节将给出考虑关节约束后机械臂的阻尼最小二乘逆运动学求解方法. 对于第i个关节,其关节角的允许范围为: 定义函数如下 (5) 其中θε>0关节角缓冲范围. 将优化问题(1)修改为 (6) 其中Λ(θ)∈RL×L为阻尼矩阵,具体形式为 Λ(θ)=λEL+Ω(θ) 其中Ω(θ)=diag{Ω1(θ1),Ω2(θ2),…,ΩL(θL)},λ由式(2)计算.上面优化问题等价于如下的最小二乘问题: 上面最小二乘的解为 容易证明上述解是Err(θ)在θ处的下降方向. 其中dT0>0为初始更新步长, 其中αθ∈(0,1).因此,考虑关节约束时,需要将算法1中的初始更新步长设置为dTmax.这样可以避免更新步长过大,从而导致关节角超出其允许范围. 除了本章给出的算法,目前已有多种处理关节约束的逆运动学算法,比如文献[7][18][19][20].文献[7][18][19]中的算法本质是一种雅克比伪逆法,由第3节可知当雅克比矩阵接近行不满秩时,算法可能出现震荡甚至发散.而文献[20]没有考虑最大更新步长,并不能严格保证关节角不超出其允许范围,在某些极端情况求解得到的关节角会超出其允许范围.相比之下,本文中的算法在阻尼矩阵和最大更新步长的限定下,可以保证关节角保持在允许范围以内. 本文给出算法的一大优势是不用考虑阻尼系数的选取问题,本小节将给出两个仿真算例来说明这个问题.考虑一个8连杆串联机械臂,其几何参数如表1所示,关节角的允许范围如表2所示. 机械臂末端初始位置为pe=[1.149 0 -0.323]T;机械臂末端初始姿态MRP为re=[-0.395 1 0.163 7 0.163 7]T.给定末端理想位置和姿态如下 表1 机械臂几何参数Tab.1 Parameters of the manipulator 表2 机械臂关节允许范围Tab.2 The range of manipulator’s joint angle 采用本文介绍的阻尼最小二乘法进行求解,其中阻尼常数设置为λc=0.05.仿真结果如图2、图3和图4所示,从中可以看出循环计算10次后末端误差收敛到可以接受的范围内,而且关节角都没有超出允许范围. 如果将其设置为λc=5,重新进行仿真,结果如图5~图7所示,从中可以看出循环计算178次后末端误差收敛到可以接受的范围内,而且关节角都没有超出允许范围. 容易看出,不论阻尼常数如何,两个算例都有指数级别的收敛速度. 这很好的反应了算法的稳定性. 但是第二个算例由于阻尼常数增大导致收敛速度变慢.而第一个算例,由于阻尼常数较小,从而导致更新步长较短(算法 1迭代次数多). 图2 当阻尼常数为0.05时机械臂关节角Fig.2 The trajectories of joint angle (λ=0.05) 图3 当阻尼常数为0.05时末端误差曲线Fig.3 The error curve (λ=0.05) 图4 当阻尼常数为0.05更新步长Fig.4 The trajectory of step length (λ=0.05) 图5 当阻尼常数为5时机械臂关节角Fig.5 The trajectories of joint angle (λ=5) 图6 当阻尼常数为5时末端误差曲线Fig.6 The error curve (λ=5) 图7 当阻尼常数为5更新步长Fig.7 The trajectory of step length (λ=5) 本文提出了一种阻尼最小二乘算法,不同于经典的阻尼最小二乘算法,该算法不依赖于阻尼常数的选取.只要阻尼常数为正数,通过适当选取更新步长,就可以保证算法的收敛性.此外本文还考虑了存在关节约束问题,给出了一种保证关节角不超出其的允许范围的阻尼最小二乘算法.最后本文给出了两个仿真算例,算例表明,只要阻尼系数大于0,算法就能保证稳定稳定性和收敛性.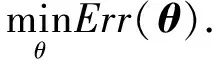


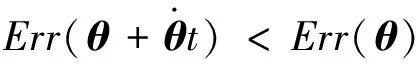

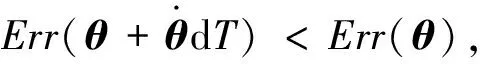
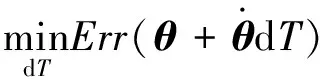

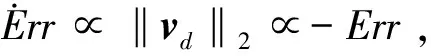

4 考虑关节约束的机械臂逆运动学求解方法

5 仿真算例


6 结 论

