柔性空间机械臂在轨操作仿真与分析*
黎 凯,张 尧,陈余军
0 引 言
空间机械臂可以完成航天器模块更换、空间站装配、故障维修、燃料补给等多种复杂的空间任务,已经成为航天器在轨服务和空间操作的重要基础[1-2].空间机械臂的应用提高了任务的灵活性,延长卫星使用寿命的同时降低了任务成本,对经济、国防和空间技术的发展具有重要意义.
空间机械臂通常安装于服务航天器上,因此对带有柔性附件的空间机械臂系统进行动力学分析,可以了解空间机械臂在轨操作过程的特点.Hu等[3-4]采用Kane方程对以变速控制力矩陀螺作为执行机构的柔性空间机械臂进行动力学建模,其中利用假设模态法描述机械臂臂杆的弹性变形,考虑了基座的影响但并未考虑挠性附件.文献[5-6]利用拉格朗日方程对考虑关节柔性的机械臂进行动力学建模,但文中认为机械臂的基座固定,且未考虑挠性附件.夏新会等[7]利用基于Kane方程的递推组集算法建立空间机械臂系统的动力学模型,但文中将基座视为固定,且未考虑机械臂臂杆的变形和挠性附件的影响.为反映基座与机械臂的相互作用,同时符合空间机械臂系统的实际情况,应当建立漂浮基座空间机械臂的动力学模型,文献[3-4,8-10]对自由漂浮的空间机械臂系统建立了动力学模型,考虑了基座与机械臂的耦合特性.在上述机械臂动力学建模的研究中,均未考虑航天器上挠性附件的影响.
在空间机械臂的控制研究方面,JIA等[11-12]设计了自适应滑模控制器实现基座的位姿控制和机械臂的轨迹跟踪控制,但在控制器设计时将基座和机械臂一同考虑,即基座和机械臂的控制分别需要机械臂和基座信息的反馈.荣吉利等[13]采用LQR-PD联合控制策略对柔性机械臂的关节轨迹进行跟踪,同时抑制臂杆末端的残余振动,但其中并未对基座加以控制.机械臂的柔性关节和柔性臂杆会使得机械臂产生振动,为提高机械臂的工作性能需要对机械臂振动进行主动控制或抑制,文献[14-18]设计了不同的控制方法对机械臂的振动进行控制或抑制.空间机械臂系统可能存在未知内部扰动和外部扰动,文献[19-20]利用扩张状态观测器对扰动进行观测并给予补偿,提高了系统的抗扰性能,实现空间机械臂的轨迹跟踪控制任务.在以上的控制方法中,通常将基座和机械臂一起考虑,即基座的控制需要机械臂关节运动的反馈,机械臂关节的控制需要基座位姿的反馈,或者不考虑基座的影响.但对于空间机械臂在轨操作任务而言,基座的姿态控制和机械臂的控制通常独立进行,即基座在进行姿态控制时不需要机械臂关节运动的实时反馈,并且机械臂在进行关节运动的控制时也不需要基座姿态信息的反馈,所以基座和机械臂的控制器设计需分开进行.
本文对带有挠性附件的航天器利用柔性空间机械臂捕获目标航天器进行研究,首先考虑挠性附件以及机械臂的变形,建立漂浮基座空间机械臂系统的动力学模型,其次给出采用修正的罗德里格斯参数描述机械臂末端姿态的轨迹规划方法,其中考虑了目标相对运动的补偿,然后将反馈控制与扩张状态观测器结合,分别设计航天器的姿态控制器和机械臂的轨迹跟踪控制器,使得基座和机械臂的控制可以独立进行,最后完成了系统的闭环控制仿真与分析.
1 动力学模型的建立
服务航天器利用机械臂对目标航天器进行操作的示意图如图1所示,首先利用服务航天器上的机械臂1对目标航天器进行捕获,然后机械臂1将目标航天器移动至与服务航天器保持一定的距离处,此时机械臂1各关节锁定,之后机械臂2抓取目标航天器上的模块并将其安装至服务航天器上.
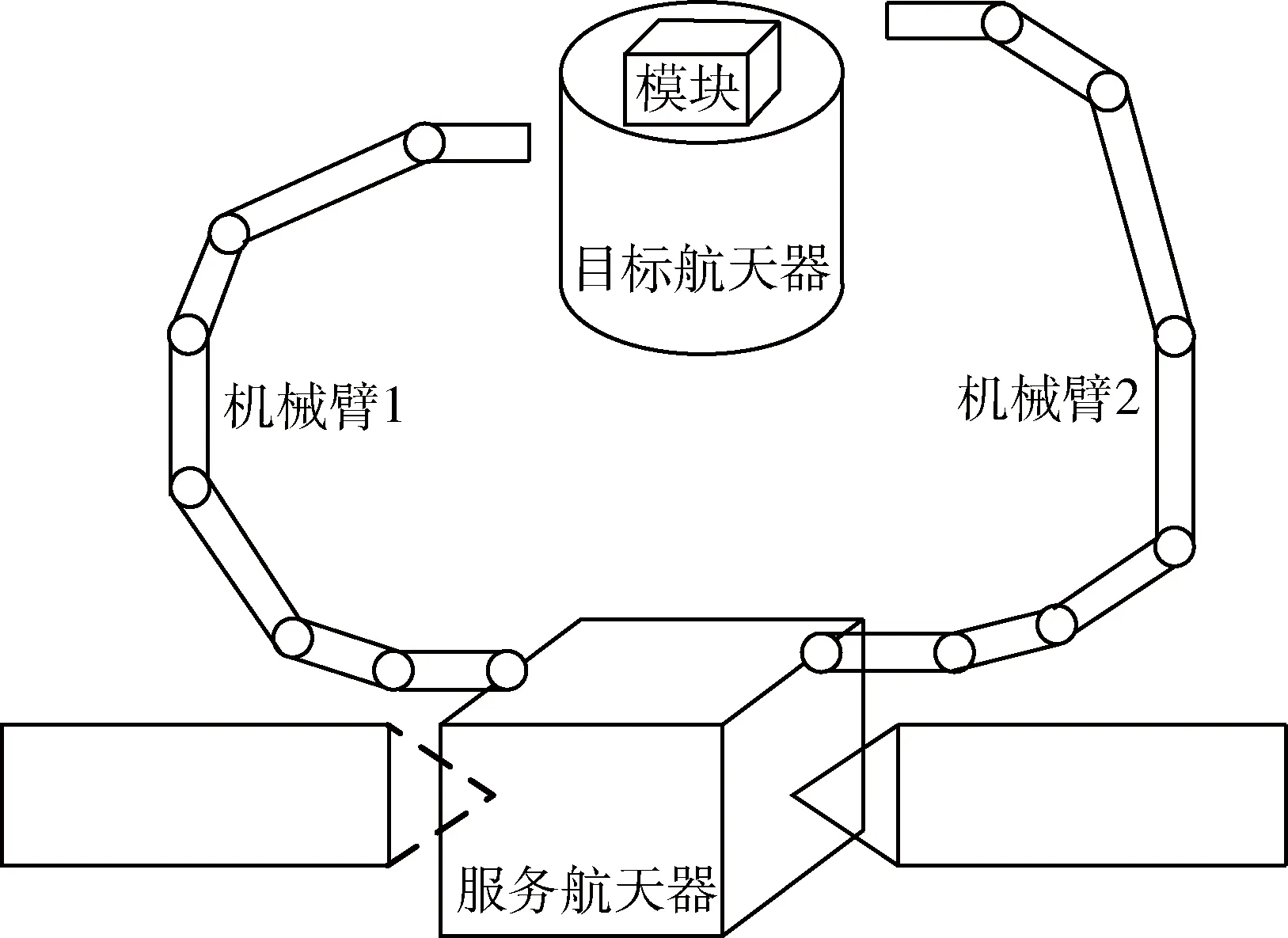
图1 机械臂操作示意图Fig.1 Space manipulators operate on target spacecraft
本文的研究不考虑机械臂与目标航天器以及模块之间的相互作用,即认为机械臂到达捕获点便完成对目标的捕获或抓取,之后目标航天器或模块便与机械臂的最末端固连,因此在建立系统的动力学模型时仅考虑服务航天器以及其上安装的机械臂.对图1所示的服务航天器,假设其由中心刚体、挠性附件以及两部七自由度柔性机械臂组成,采用Kane方程建立此系统的动力学方程.Kane方程的基本形式为
(1)
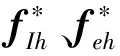
服务航天器上的柔性机械臂为仅考虑臂杆的变形,根据假设模态法,臂杆和柔性附件上任意一点的弹性位移可表示为
u=Φq
(2)
式中,Φ为仅跟位置有关的3×l阶矩阵,q为l×1列阵,代表模态坐标.
系统的动力学方程为
(3)
相关参数定义为
K=diag{06×6,014×14,Km1,Km2,Ka1,Ka2}
C=diag{06×6,014×14,Cm1,Cm2,Ca1,Ca2}
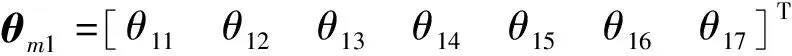
对服务航天器采用3-1-2旋转顺序的欧拉角描述其姿态,记φ、θ和ψ分别表示服务航天器本体坐标系相对轨道坐标系的滚动、俯仰和偏航角,则服务航天器的姿态运动学方程为
(4)
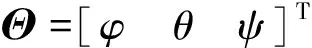
2 机械臂轨迹规划
机械臂在捕获目标航天器、移动目标航天器、抓取模块以及安装模块的过程中,对其末端位置和姿态均有一定的要求,而机械臂的控制通常针对关节进行,因此,需要将机械臂末端的位置和姿态运动规律转化为各个关节的运动规律,便于对机械臂实施控制.
考虑到机械臂末端的位置和姿态以及目标航天器的位置和姿态通常是由服务航天器测量得到,因此对机械臂末端位置和姿态的描述均相对服务航天器进行.另外,机械臂在操作过程中其末端姿态变化范围较大,所以采用修正的罗德里格斯参数(MRPs)对其末端姿态进行描述.机械臂的轨迹规划可分两步进行,首先规划机械臂末端位置和姿态的运动规律,然后再计算机械臂各关节的运动规律.
2.1 机械臂末端相对位置与姿态
如图2所示,Obxbybzb为服务航天器本体坐标系,Oexeyeze为第7节机械臂本体坐标系,假设机械臂的末端点在第7节机械臂本体坐标系中的位置为re,则根据图2所示的关系,机械臂的末端点相对服务航天器本体坐标系的位置可写为
(5)
式中,Abi表示第i节机械臂本体坐标系至服务航天器本体坐标系的转换矩阵.由于机械臂1和机械臂2的末端点相对服务航天器的位置的计算过程独立且类似,因此这里不区分机械臂1和机械臂2,而仅以其中一部机械臂进行分析.
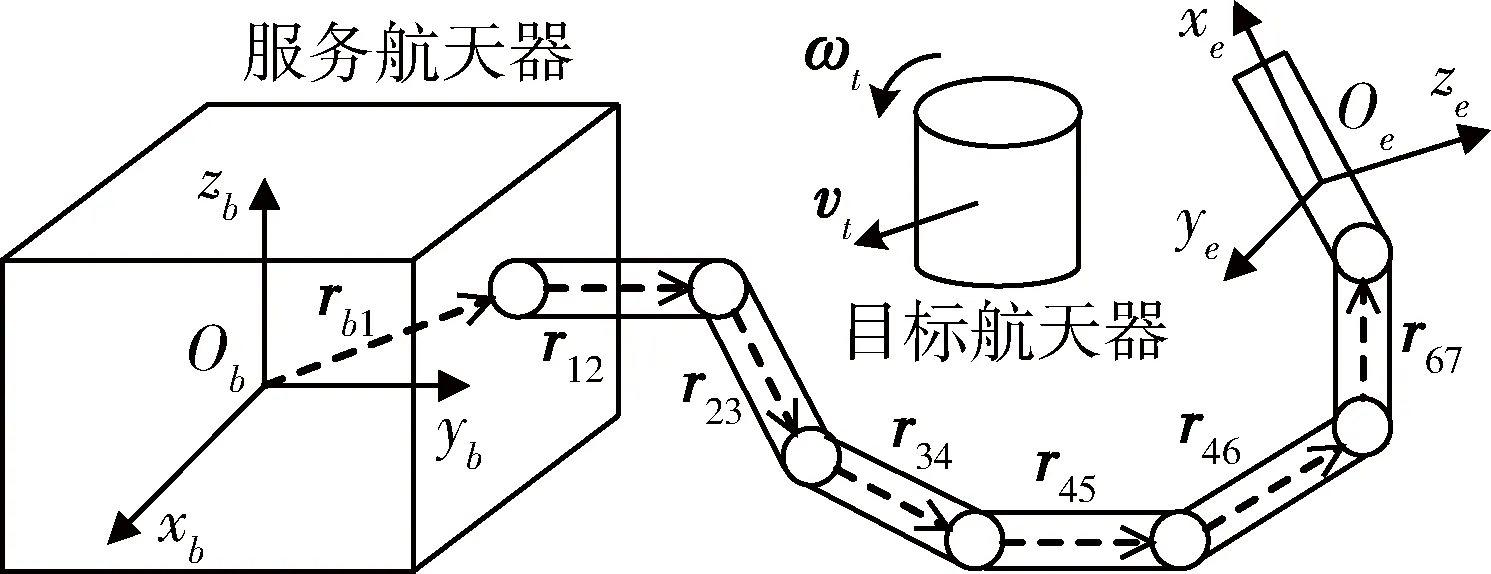
图2 机械臂末端位置与姿态描述Fig.2 Description of the position and attitude of end-effector
对式(5)求导,可以得到机械臂末端点相对服务航天器的速度为
(6)
式中:Jve为机械臂关节角速度到末端速度的3×7雅克比矩阵;θm为机械臂关节角列向量.
假设σ为机械臂末端作用器相对服务航天器的MRPs,则机械臂末端的相对姿态运动学方程为
(7)
式中,ωeσ为机械臂末端相对服务航天器的角速度;H(σ)为
(8)
另一方面,机械臂末端相对服务航天器的角速度可用关节角度参数表示为
(9)
式中,A7i表示第i节机械臂本体坐标系至第7节机械臂本体坐标系的转换矩阵;ηi为描述第i节机械臂转轴方向的单位向量在其本体坐标系下的表示.
前述两种方法所描述的机械臂末端的相对角速度应相等,将它们均表示在服务航天器的本体坐标系下有
R(σ)ωeσ=Ab7ωe
(10)
式中:R(σ)为由MRPs确定的从坐标系Oexeyeze至坐标系Obxbybzb的转换矩阵.结合式(7)、式(9)与式(10),可以得到
(11)
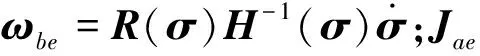
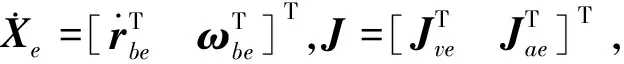
(12)
式(12)给出了机械臂末端相对速度、相对角速度与机械臂关节角度参数的关系.
2.2 机械臂末端位置与姿态规划
在规划机械臂末端位置和姿态时,通常已知位置和姿态的初始值与终端值,采用五次多项式的方法对末端位置和姿态进行规划.在机械臂对目标航天器进行捕获的过程中,目标航天器相对服务航天器可能存在相对运动,如图2所示,目标航天器相对服务航天器可能存在相对速度vt与相对角速度ωt,因此在规划过程中,末端位置和姿态的终端值是时变的.但目标航天器相对服务航天器的速度与角速度通常可以由服务航天器测量得到,所以在五次多项式的规划方法中可以对相对速度与相对角速度进行补偿.
假设机械臂末端相对位置或相对姿态参数在初始时刻t0的期望值与实际值分别为sd(t0)与sr(t0),令Δs(t0)=sd(t0)-sr(t0)为初始时刻的相对位置或姿态误差,则机械臂轨迹规划的目的是使得在结束时刻tf有Δs(tf)=0.将机械臂末端相对位置和姿态参数按照如下形式进行规划
(13)
式中,v(t)和a(t)分别表示相对位置和姿态参数的速度与加速度;A、B、C、D、E和F为多项式的系数,可根据如下的初始条件和终端条件确定
(14)
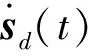
(15)

ac(t)=a(t)
(16)
需要说明的是,对于目标航天器的相对角速度的测量值,应先按照式(7)转化为MRPs的变化率,再根据式(15)进行相应的修正.
2.3 机械臂关节运动规划
式(12)中的雅克比矩阵J为6×7矩阵,因此对于给定的机械臂末端相对速度与相对角速度,满足式(12)的机械臂关节角速度并不唯一,这里采用广义逆的方法对机械臂关节角速度进行求解,即
(17)
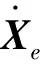
机械臂的关节角度为
(18)
式中:θm0为机械臂关节角度的初始值.
为便于对机械臂的控制,还需给出机械臂的关节角加速度,对式(17)求导得
(19)
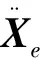
3 控制器设计
服务航天器利用机械臂进行目标航天器捕获或模块安装时,需要对服务航天器的姿态进行稳定控制,同时使得机械臂对期望的轨迹实现跟踪.观察式(3)所示的系统动力学方程,服务航天器的平动、转动,机械臂的转动、振动,柔性附件的振动相互影响,因此在进行服务航天器的姿态控制和机械臂的轨跟踪控制时需将这种耦合特性予以考虑.在实际工作情况中,柔性附件和机械臂的振动通常不进行控制,并且服务航天器的姿态控制和机械臂的控制通常独立进行,所以以下将分别设计服务航天器的姿态稳定控制器和机械臂的轨迹跟踪控制器.
3.1 服务航天器姿态稳定控制器
将式(3)给出的动力学方程中对应服务航天器姿态运动的方程单独提出,表示为
(20)
进一步将式(20)改写为
(21)
式中:g(ω)为非线性项Fnr中与服务航天器转动相关的主要部分,其仅与服务航天器的角速度和机械臂关节角度的初始值有关;drn为服务航天器平动、机械臂转动和振动以及柔性附件振动对服务航天器转动的耦合项,与Fnr中除去g(ω)剩下的部分之和,可将drn视为扰动.
在式(21)中,Ir不仅与机械臂的关节角度有关,还与柔性附件和机械臂的弹性位移有关,但是弹性位移难以测量,并且机械臂的关节角度在服务航天器的姿态控制中不易实时更新,所以不妨认为在姿态控制的过程中只能获得机械臂关节角度的初始值,因此可以将Ir写为
Ir=Ir0+ΔIr
(22)
式中:Ir0为不考虑弹性位移且机械臂关节角度始终为其初始值时的惯量矩阵,为常值;ΔIr为由弹性位移和机械臂关节角度变化引起的惯量矩阵的改变.
结合式(21)和式(22)可以得到
(23)
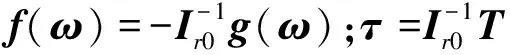
以服务航天器的角速度的测量值作为输入,设计如下的二阶扩张状态观测器对式(23)中的未知扰动dr进行估计
(24)
则当参数αb、δb、βb1和βb2的选择满足一定条件时有Zb1→ω,Zb2→dr.因此对于式(23),可以设计等效控制量为
τ=τ0-Zb2
(25)
所以式(23)可写为
(26)
对式(4)求导并结合式(26)可以得到
(27)
据此可以设计τ0为
(28)
式中,Kpb与Kdb为PD控制器参数,选取合适的值可以使得服务航天器的姿态趋于稳定.
为了使控制量中不包含高频部分,需要对式(25)中的控制量进行滤波,设计一阶线性滤波器如下:
(29)
式中,λb>0,可根据柔性体的模态频率选取合适的值.
服务航天器的实际姿态控制力矩为
T=Ir0τb
(30)
服务航天器姿态稳定控制器对应的控制框图如图3所示.
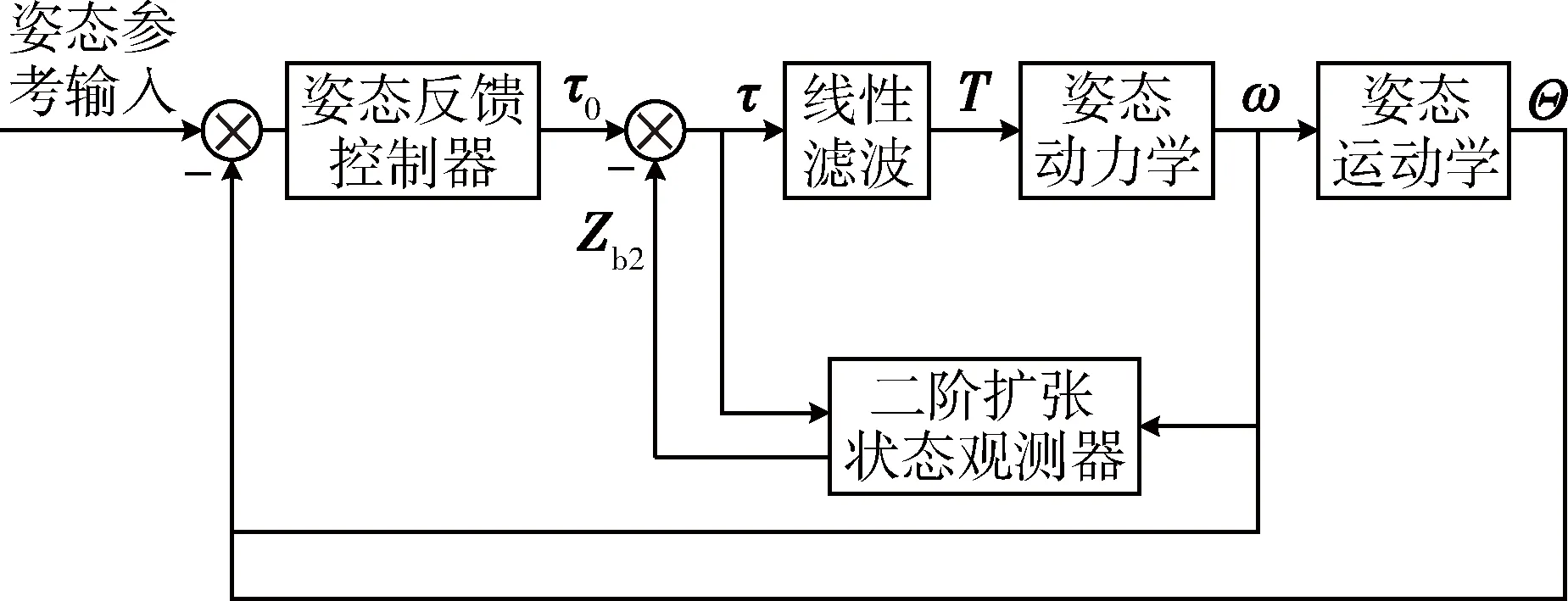
图3 服务航天器姿态控制框图Fig.3 Block diagram of the attitude controller
3.2 机械臂轨迹跟踪控制器
按照服务航天器姿态稳定控制器的设计过程,可以类似地设计机械臂的轨迹跟踪控制器.首先将式(3)中对应机械臂转动的方程进行改写
(31)
式中:Mm0为不考虑弹性位移时的质量矩阵,仅跟机械臂的关节角度有关;ΔMm为由弹性位移引起的质量矩阵的改变;dmn为扰动项.
式(31)可进一步改写为
(32)
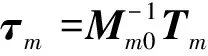
以机械臂的关节角速度作为输入,利用二阶扩张状态观测器对式(32)中的未知扰动dm进行估计,将估计值在反馈控制器中进行补偿,可以实现机械臂的轨迹跟踪控制,图4给出了机械臂轨迹跟踪的控制框图.

图4 机械臂轨迹跟踪控制框图Fig.4 Block diagram of the manipulator controller
图4中的部分设计过程如下:
τm=τm0-Zm2
(33)
式中,Zm2为二阶扩张状态观测器对未知扰动dm的估计值.
(34)
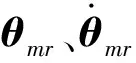
对控制量τm进行滤波
(35)
式中,λm>0,可根据柔性体的模态频率选取适当的值.
机械臂的实际关节控制力矩为
Tm=Mm0τc
(36)
4 数值仿真
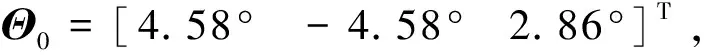

表1 系统质量与惯量参数Tab.1 Mass and inertia parameters
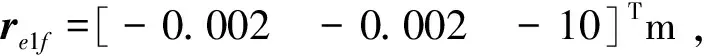
仿真中考虑机械臂较长的两节臂杆的变形,两节臂杆长度均为4 m,取前两阶模态进行分析,模态频率为10.21 Hz.服务航天器上的两个太阳翼对称安装,取前两阶模态进行分析,其第一阶和第二阶模态频率分别为0.01 Hz和0.031 Hz.仿真时间步长为0.005 s.在机械臂1捕获目标和移动目标的两个阶段,滤波参数λb分别设置为10和5,λm分别为5和1.在机械臂2抓取模块和安装模块的两个阶段,滤波参数λb都设置为10,λm分别为5和2.上述滤波参数的选取一方面根据机械臂的模态频率确定,另一方面,考虑到机械臂1在捕获目标并与目标固连后,其末端质量与惯量突然增大,导致系统的振动频率降低,所以捕获目标后的滤波参数减小.但是由于模块的质量远小于目标航天器的质量,所以机械臂2安装模块过程的滤波参数变化小于移动目标过程的滤波参数变化.
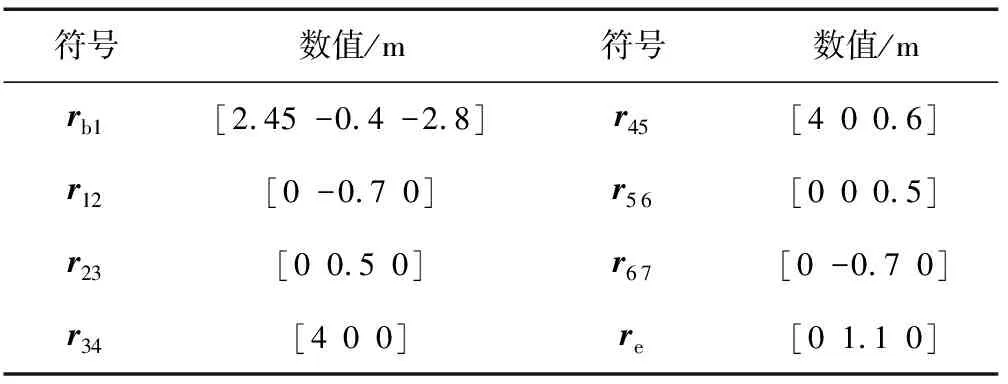
表2 机械臂几何构型参数Tab.2 Geometry data of manipulator
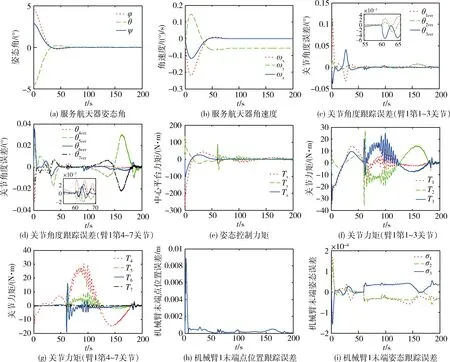
图5 机械臂1捕获目标航天器(无相对运动)的仿真结果Fig.5 Simulation results of capturing the target spacecraft (without relative motion) using manipulator 1
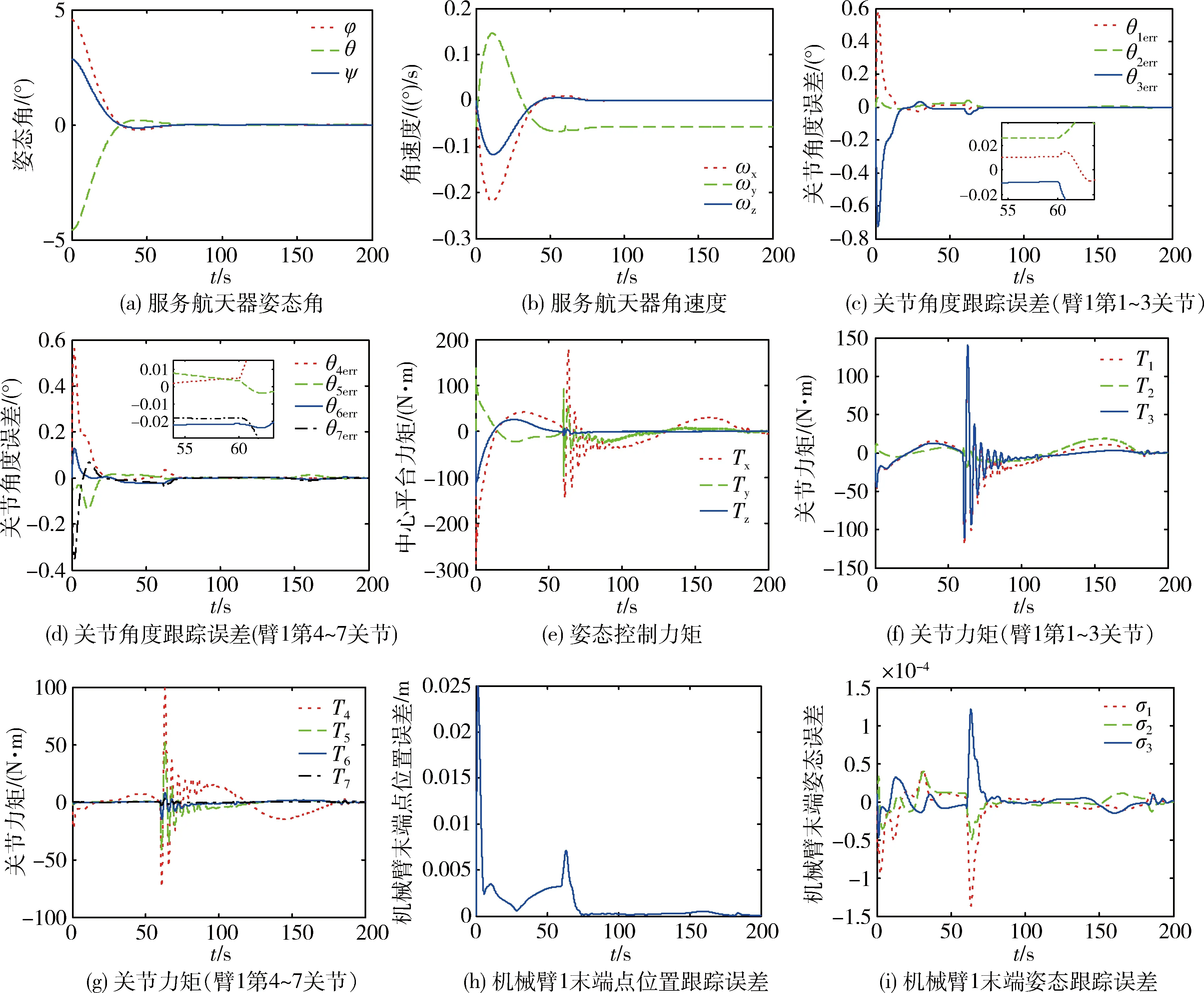
图6 机械臂1捕获目标航天器(有相对运动)的仿真结果Fig.6 Simulation results of capturing the target spacecraft (with relative motion) using manipulator 1
图5与图6分别给出了两种工况的仿真结果.在两种工况下,服务航天器的姿态在机械臂1捕获目标航天器的过程中均能趋于稳定.由于目标航天器的相对运动,第二种工况下的关节角度跟踪误差在初始阶段和捕获时刻(60 s)均比第一种工况的要大.在机械臂1捕获目标航天器的时刻,认为目标航天器与机械臂1的末端固连,此时机械臂1末端的质量和惯量发生突变,导致捕获时刻的姿态控制力矩与关节驱动力矩发生较大变化,并且目标航天器的相对运动使得这种变化更为明显.在机械臂1捕获目标航天器的时刻及之后的移动过程中,其末端相对位置和姿态误差均较小,证明机械臂的轨迹跟踪控制器有效.
图7给出了机械臂2安装模块的仿真结果.可以看出,在机械臂2安装模块的过程中,服务航天器的姿态趋于稳定.同样由于机械臂2抓取模块后即与模块固连,导致姿态控制力矩在抓取时刻发生较大变化,但由于模块的质量相对于目标航天器较小,故机械臂2的关节驱动力矩在抓取时刻并未出现较大变化.
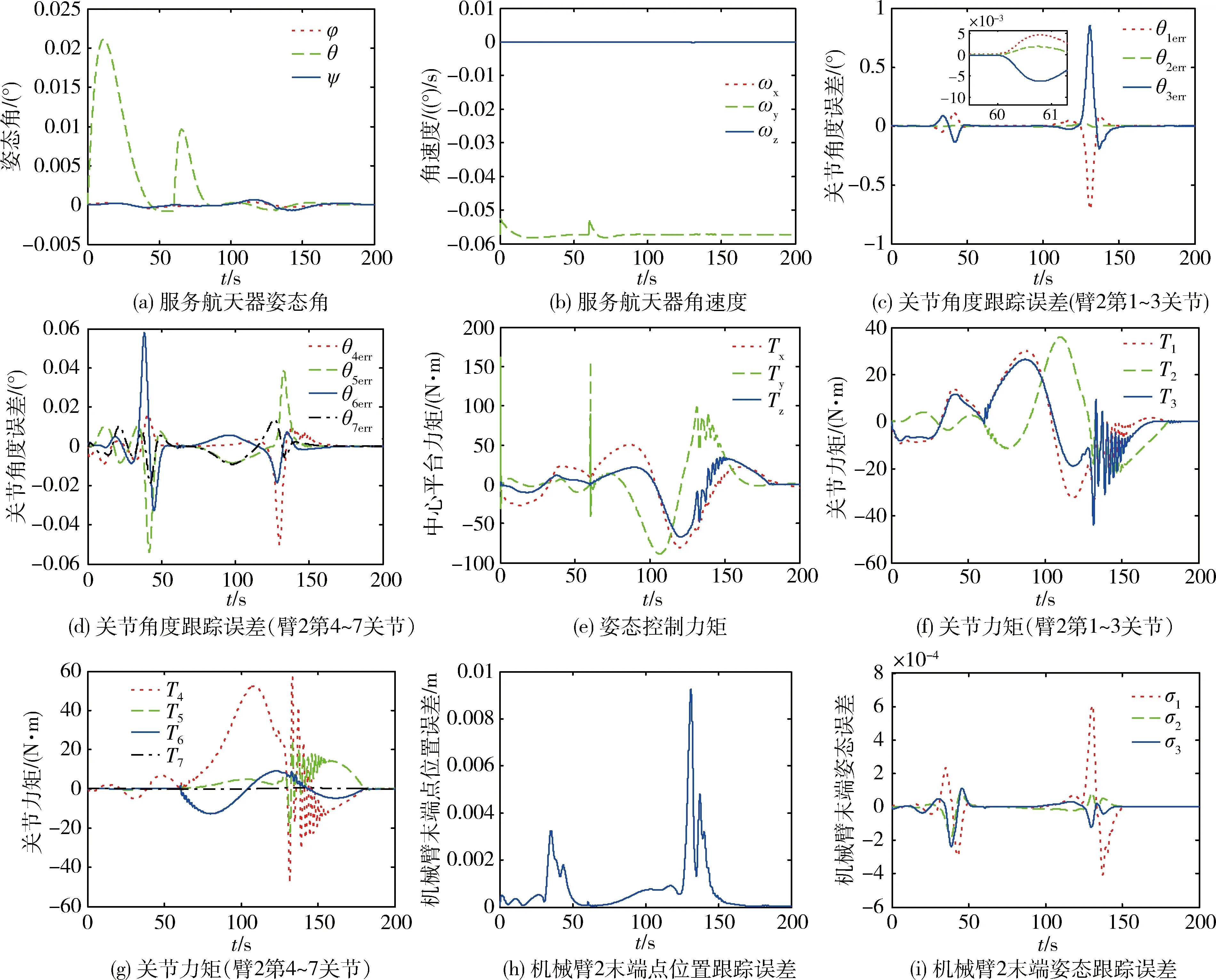
图7 机械臂2安装模块的仿真结果Fig.7 Simulation results of assembling module using manipulator 2
5 结 论
本文对柔性空间机械臂捕获目标航天器和安装模块的在轨操作过程进行仿真分析.建立了带有挠性附件的柔性空间机械臂系统的动力学模型,采用修正的罗德里格斯参数描述机械臂末端的相对姿态,将反馈控制与扩张状态观测器结合,设计了姿态稳定控制器和机械臂轨迹跟踪控制器.对机械臂捕获目标航天器和安装模块的过程进行数值仿真,验证了所设计控制器的有效性,同时发现目标航天器的相对运动使得系统在捕获时刻的控制指令发生较大变化.

