空间机器人抓捕目标碰撞后的复合体稳定控制*

韩 冬，黄攀峰，刘习尧

0 引 言

航天器在发射或工作过程中可能出现设备故障，如太阳能帆板未能有效展开、推进剂耗尽等，这会使其失去姿态控制能力,但大部分情况下其有效载荷仍可以继续工作,通过航天器在轨维修可以解决航天器故障，延长航天器使用寿命[1].空间机器人是一种完成航天器在轨服务任务的有效设备，可以完成包括燃料加注、在轨维修、设备更换、轨道垃圾清除等任务，SUMO/FREND和DEOS就是典型的空间机器人在轨服务项目[2-3].空间机器人完成服务任务一般分为4个阶段[4]，分别是观测与估计、接近与停靠、目标捕获、复合航天器稳定控制.在观测与估计阶段完成目标的运动信息获取，包括位置、姿态、线速度与角速度等，估计目标运动轨迹，辨识目标惯性参量等以决定捕获目标时机与位置；在接近与停靠阶段，空间机器人平台按规划轨迹到达停靠位置并规划机械臂到达目标捕获位置；目标捕获阶段包括空间机器人与目标卫星的物理接触，主要目的是捕获运动或者可能旋转的目标，一旦目标被成功捕获，空间机器人与目标形成复合航天器，通过空间机器人平台的执行机构实现对复合航天器的稳定控制.

目前国内外针对结构突变复合航天器稳定的研究较少，概括起来主要分为两类.第一类假定抓捕目标动力学参数已知或者可以被辨识出，通过角动量分配或目标重定位等方法吸收角动量.文献[5]提出了机械臂与反作用飞轮协调控制思想，采用“Bias Momentum Control”和“Distributed Momentum Control”方法完成了目标抓捕后的复合航天器稳定控制，实现了基座的姿态稳定.刘厚德等[6]采用关节阻尼控制与关节角轨迹参数化协调控制，实现了对系统角动量的管理和协调分配.韦文书等[7]采用滑模变结构控制方法，首先将捕获后的目标航天器进行重定位，然后启动自动配平模块，使之恢复到平衡状态，从而消除系统参数突变所带来的各种不利影响.

第二类考虑抓捕目标动力学参数未知，通过鲁棒控制或自适应控制方法,实现对失效航天器的姿态接管控制.文献[8]采用了低复杂度预设性能控制方法，该方法无需对模型的具体参数进行先验估计或在线辨识，通过预设系统的性能指标，实现了在未知系统参数条件下的稳定控制.文献[9]通过自适应动态逆控制来重构服务航天器的姿态接管控制律，从而使得在目标动力学参数未知的情况下，实现了组合航天器的稳定控制.文献[10]引入连接系绳，通过系绳拉力，消除碰撞后角动量对复合航天器稳定的影响，解决了执行机构可能出现的饱和问题.文献[11]通过机械臂协调控制，实现组合航天器的姿态稳定.文献[12-14]采用了参数估计结合控制系统重构的方法.

本文研究的空间机器人抓捕旋转目标后复合航天器稳定问题，与传统的组合航天器稳定控制不同，主要体现在两个方面：1)已有的研究方法多采用机器人自身的稳定执行机构完成复合航天器稳定，未考虑新复合航天器参数突变对原有执行机构的影响.由于抓捕后目标航天器与空间机器人形成的复合航天器属于变参数变构型的非线性时变系统，用原有航天器稳定控制的执行机构要来稳定新的对象，需要进行控制系统重构和控制重分配.本文借鉴多体航天器和模块化航天器的研究思路提出反作用轮构型重构方法，解决参数突变问题.2)已有的关于复合航天器稳定控制的研究均未考虑抓捕过程中碰撞对稳定控制的影响.由于空间机器人测量传感器的测量误差及抓捕执行机构的系统误差，抓捕过程中的碰撞难以避免，会造成空间机器人在短时间受到较大碰撞力，如不加控制将导致系统失稳.本文利用滑模变结构控制系统鲁邦性强的特点，提出了反步积分滑模控制方法，解决了滑模控制器对偏差过分敏感问题，反步积分滑模控制方法采用双环积分控制，外环控制器实现空间机器人姿态的保持，内环控制器实现对角速度脉冲的抑制，从而实现对碰撞后复合航天器系统的稳定控制.

1 复合航天器姿态偏差动力学

1.1 问题描述

为了提高航天器姿态稳定性能，对于中高轨道的航天器，目前普遍采用了飞轮三轴姿态稳定系统，它的工作原理是动量矩定理，即航天器的总动量矩矢量对时间的导数等于作用在航天器上外力矩矢量之和.由于飞轮是以内力矩作为控制力矩，所以当外力矩矢量和为零时，航天器总动量矩守恒.于是通过改变飞轮的动量矩矢量，可以吸收航天器其余部分多余的动量矩矢量，从而达到航天器姿态控制的目的.由于其输出的控制力矩连续，消耗的能源可再生等优点，使其成为航天器姿态控制的首选执行机构，本文研究利用空间机器人的飞轮三轴姿态稳定系统来实现对碰撞后复合航天器的稳定控制.复合航天器主要包括空间机器人(包括基座与操作臂)和抓捕目标，其结构如图1所示.

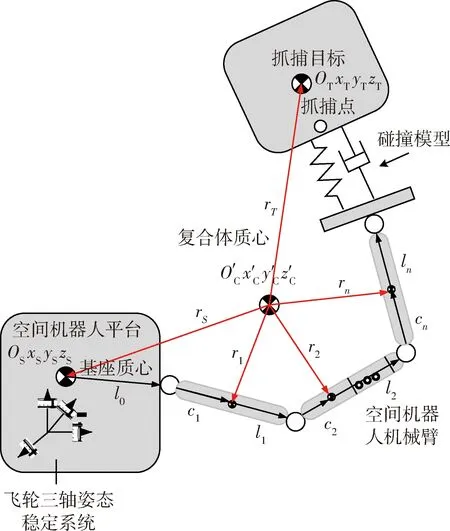
图1 空间机器人抓捕目标模型Fig.1 Model of space robot capturing a target

为了对复合航天器稳定控制问题进行合理研究，不失一般性，本文定义如下基本假设：A1抓捕目标因燃料耗尽或太阳能帆板未能有效展开等原因，自身姿态控制系统无法工作.A2空间机器人的飞轮三轴姿态稳定系统由4个反作用轮构成，其安装位置及配置方式均已知.A3操作臂在抓捕前构型已知，在完成抓捕后锁定构型，在复合航天器稳定控制期间其构型不再改变.A4空间机器人、操作臂及抓捕目标的质量特性已知或者可以通过辨识方法获得.

本文研究碰撞条件下复合航天器稳定控制技术，需要解决以下4个问题：1)复合航天器的惯量主轴与主惯量求解；2)碰撞过程建模与碰撞力分析；3)复合航天器控制器设计；4)反作用轮的构型重构及控制力矩重分配.

1.2 复合航天器姿态动力学与碰撞建模

空间机器人在完成目标抓捕后形成复合航天器，可以等价为操作臂末端执行器质量特性参数发生了改变，形成复合航天器的惯性参量及惯量主轴均与空间机器人不同，这会对飞轮三轴姿态稳定系统的工作造成影响，因此需要计算复合航天器的惯性参量及惯量主轴.

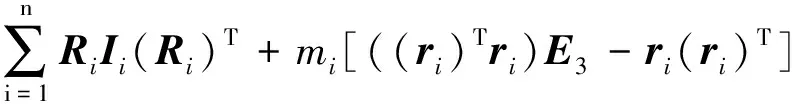
(1)

式中：E3为3阶单位矩阵，mS、mT和mi分别为空间机器人平台、目标航天器及空间机械臂连杆i的质量；IS和IT为空间机器人平台和目标航天器相对于各自本体坐标系的惯性张量；Ii为空间机械臂的连杆i相对于其自身连杆质心坐标系的惯性张量；矩阵RS、RT、Ri分别为空间机器人平台、目标航天器、空间机械臂连杆i的姿态旋转矩阵；rS、rT和ri分别为服务航器、目标航天器、空间机械臂连杆i的质心位置矢量.

为将复合航天器惯量对角化，定义复合航天器惯量在惯量主轴坐标系Ocxcyczc中表示为I,复合航天器本体坐标系到惯量主轴坐标系的变换矩阵为Φ,两坐标系的质量元位置矢量分别为ρ和ρ′,则两者关系为

ρ=Φρ′

(2)

因此，可得两坐标系之间的惯量矩阵转换关系为：

=ΦI*ΦT

(3)

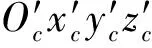
考虑到空间机器人装备4个反作用轮用于姿态稳定，则复合航天器在惯量主轴坐标系下描述的角动量可表示为：

H=Iω+CJwΩ

(4)

式中,I为复合航天器惯量主轴坐标系下的惯量矩阵，ω为惯性系下表示的复合航天器姿态角速度Jw为飞轮组惯量阵Jw=diag{Jw1,Jw2,Jw3,Jw4}，Ω为飞轮组转速矢量Ω=[Ω1Ω2Ω3Ω4]T，C为反作用轮构型矩阵，其各列为各反作用轮转轴在复合航天器惯量主轴坐标系中的方向余弦.

由于碰撞发生在目标捕获完成之前，在形成复合航天器前将碰撞产生的作用力矩考虑为外力矩，考虑到碰撞作用时间短，力矩大的特点，从而忽略重力梯度力矩、气动力矩等力矩影响，复合航天器和反作用轮的姿态欧拉动力学方程表示为：

(5)

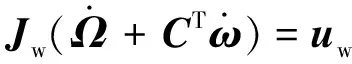
(6)

式中：uw为作用在反作用轮上的力矩；Tc为作用在组合航天器上的碰撞力产生的力矩.

根据方程(4)～(6)可以得到包含反作用轮的复合航天器非线性姿态动力学方程

(7)

空间机器人的末端执行器对目标进行抓捕过程中，不可避免的会与目标产生接触与碰撞，如图2所示，当目标进入抓捕范围后抓捕器会收拢手抓，使目标航天器与空间机器人形成复合航天器.空间机器人在碰撞力作用下姿态会发生突变，如不加以控制会导致基座失稳，造成抓捕失败，因此有必要对碰撞进行建模分析.

本文采用Kelvin模型对碰撞过程进行建模：

(8)

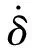
假设末端执行器的碰撞点与空间机器人质心之间的相对位置矢量为dr,则碰撞力产生的碰撞力矩为：

Tc=dr×Fc

(9)

1.3 复合航天器姿态偏差动力学

角速度的变化会导致组合体的姿态偏差，为保持复合航天器稳定，需要通过对反作用轮的控制消除姿态偏差，因此在设计姿态控制器前，需要给出复合航天器的姿态偏差动力学.

采用修正的罗德里格斯参数描述复合航天器的姿态运动学方程为：

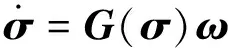
(10)

式中：σ=[σ1σ2σ3]T为修正的罗德里格斯参数，运动学方程G(σ)可以表示为：

(11)

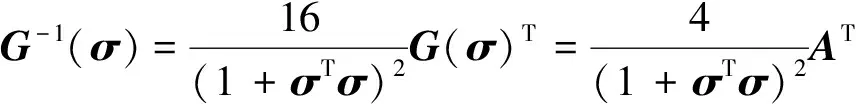
(12)

式中，

将方程(7)，(10)描述为状态空间形式：

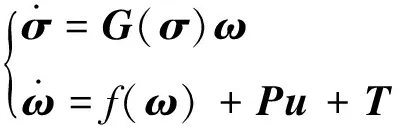
(13)

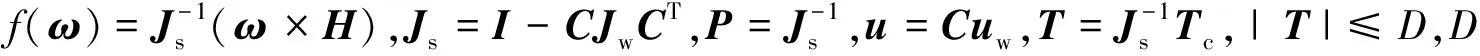
2 复合航天器稳定系统设计

空间机器人在抓捕目标过程中产生的碰撞具有碰撞位置不可预测性以及环境变量的不确定性.捕获目标后，形成的复合航天器与空间机器人本体具有不同的质量、惯量张量等特性参数，这种冲击与改变给复合航天器姿态保持带来了很大的挑战.借鉴航天器执行机构故障中的控制系统重构技术及滑模控制的高鲁棒性特点，本文提出基于反作用轮控制力矩重分配的反步积分滑模控制方法，实现对碰撞后复合航天器的姿态稳定控制，如图3所示.

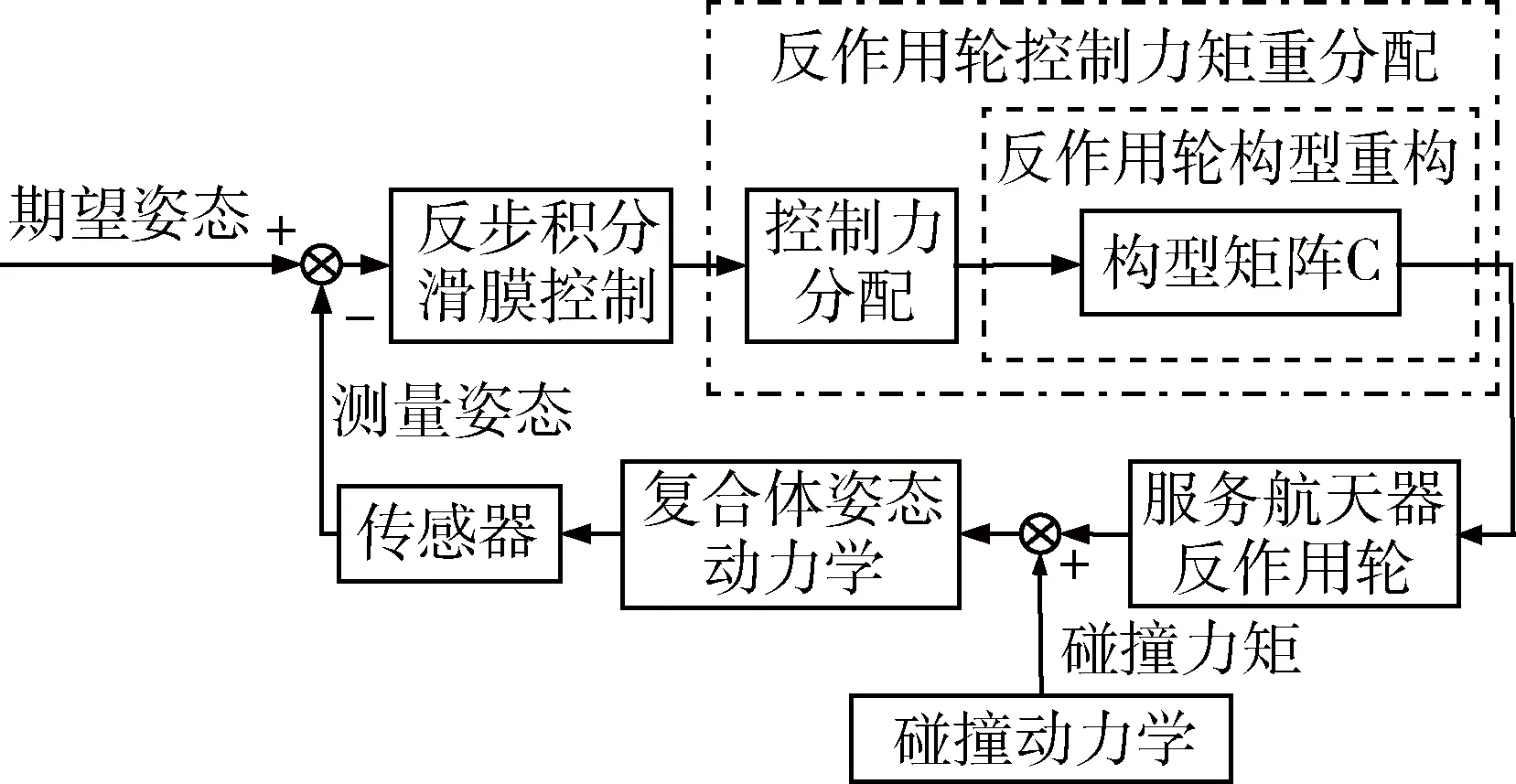
图3 复合航天器稳定控制系统框图Fig.3 Bloce diagram of stability control system

2.1 反步积分滑模控制器设计

反步法在设计不确定系统鲁棒或自适应控制器时，有明显的优势，该方法提出之后受到了众多学者的关注[15-18]，反步积分滑模控制器利用反步法思想，通过逐步递推的设计方法，引入虚拟控制量ωc作为静态补偿，将对姿态的稳定控制分解为对复合航天器姿态稳定的外环控制器和对引起姿态变化角速度稳定的内环控制器，外环采用反步积分滑模控制实现姿态的稳定，控制器产生虚拟控制量ωc,并传递给内环系统，内环则通过内环积分滑模控制律实现对虚拟控制量ωc的跟踪.控制系统机构如图4所示.

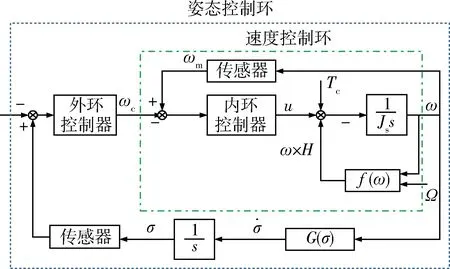
图4 反步积分滑模控制系统结构框图Fig.4 Block diagram of backstepping integral sliding mode controller

设计外环滑模面形式为：

(14)

式中：K1=diag{k11,k12,k13}为增益矩阵，通过选择合适的值可以使得系统的偏差在一个比较理想的滑模面上滑动至稳定.

取姿态角速度指令ωc作为姿态角速度ω跟踪的虚拟控制项，姿态角速度指令ωc设计为：

(15)

式中ρ1>0,

sign(so)=[sign(s1) sign(s2) sign(s3)]T.

为实现对虚拟控制量ωc的跟踪，设计内环滑模控制律u,使得ωc-ω→0,即有下式成立：

(16)

采用积分滑模设计内环滑模函数为

(17)

式中ωe=ω-ωc，K2=diag{k21,k22,k23}为增益矩阵.

根据复合航天器动力学方程设计控制律为：

(18)

式中ks>0,η>D.

在完成控制器设计的基础上，进行控制器稳定性的证明.采用构造Lyapunov函数方法证明系统稳定性，主要证明思路是首先证明外滑模面的稳定，然后证明内滑模面的收敛.

(1) 外滑模面稳定性证明

定义Lyapunov函数：

(19)

由式(14)可得：

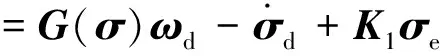
(20)

则：

(21)

(2) 内环滑模面稳定性证明

定义Lyapunov函数：

(22)

由式(17)可得：

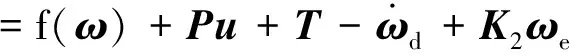
(23)

则：

=-kss2-|sT|η+sTT≤0

(24)

2.2 基于伪逆的反作用轮控制力矩重分配

控制力矩重分配问题是指在约束条件下，根据期望的控制结果，求解使得目标函数最小的冗余配置的各个执行机构的输出量.主要方法有几何控制分配、链式控制分配、饱和控制分配、广义逆控制分配等方法[19].伪逆法作为一种广义逆方法，具有输出分配最优化、任何条件下都有输出量的特点，能有效改善系统的动态性能.

反作用轮控制力矩重分配设计是根据1节计算得到的复合航天器姿态动力学模型对反作用轮进行控制力重分配，由重构解算器和可重构的反作用轮组成，重构解算器根据解算得出的复合航天器质量、质心和惯性张量计算反作用轮重构矩阵，得益于反作用轮的冗余设计，使得在不改变反作用轮物理配置的条件下，实现反作用轮重构.采用伪逆法将控制力矩在冗余配置的零动量反作用轮之间重新分配来实现复合航天器姿态稳定的控制效果.该方法主要包含反作用轮构型重构和控制力矩重分配两部分.

根据假设条件A2，空间机器人姿态由4个反作用轮调节，反作用轮的标准配置如图5(a)所示，3个工作轮安装在空间机器人的惯性主轴上，备用轮与工作轮夹角为54.74°.

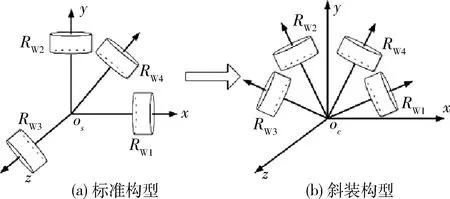
图5 不同坐标系下反作用轮配置Fig.5 Configuration of reaction wheels in different frame

由于捕获目标后形成复合航天器会改变机器人原有的惯量主轴，在新惯量主轴坐标系下反作用轮将变成斜装构型，如图5(b)所示，这会导致按原有构型分配的控制力矩不准确，因此必须重新解算控制力矩分配矩阵.

定义在空间机器人本体坐标系OSxSySzS下反作用轮构型矩阵为C*,在复合航天器惯量主轴坐标系Ocxcyczc下反作用构型矩阵为C,则可表示为：

C=ΦTC*

(25)

从而可知反作用轮控制力矩uw与反作用轮对组合航天器提供的控制力矩uc之间的关系为：

uc=-Cuw

(26)

为使得所要求的控制力矩在反作用轮上分配最优，定义如下指标：

(27)

式中：l为向量范数.

考虑到2范数分配模型能在有效分配期望控制量的基础上减少执行机构饱和状态，使得控制量分配更合理，并且2范数的解存在连续性与唯一性，因此采用2范数进行分配模型优化计算.

定义如下2范数指标：

(28)

为求解约束条件下的控制力矩平方和最小，定义新的泛函：

(29)

根据极值的必要条件可得：

(30)

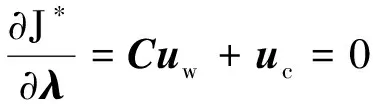
(31)

联立式(30)，(31)求解得

λ=-(CCT)-1uc

(32)

uw=-CT(CCT)-1uc=-C†uc

(33)

式中：矩阵C†=CT(CCT)-1为矩阵C的伪逆矩阵.由此可得反作用轮的力矩重分配矩阵为：

D=CT(CCT)-1

(34)

3 仿真分析

为证实所提出方法的有效性，采用如图1所示的三连杆机械臂抓捕空间目标作为研究对象，对碰撞模型及复合航天器稳定控制进行仿真研究.根据假设条件A3，机械臂在碰撞前的构型为θ=[-10° 35° 60°],空间机器人质量108 kg，目标航天器199 kg.根据假设条件A4，已知机器人及目标参数条件下，计算复合航天器在惯性主轴系下的惯量矩阵为：

采用图5所示反作用轮配置方案，求得反作用轮配置矩阵为：

C=

计算反作用轮控制力矩重分配矩阵D为：

不失一般性，假设初始姿态角σ=[0 0 0]T初始角速度ω=[0 0 0]T,期望角度、角速度均为零.单个反作用轮的转动惯量为0.338 kg·m2，最大转速为500 r/m，最大角动量为17.8 N·m·s，最大输出力矩为1 N·m.根据已有研究结果，抓捕点轨迹预测偏差导致了抓捕过程中的碰撞问题[20]，速度估计偏差初值为v0=[0.029 0.021 0.016]Tm/s,碰撞点与空间机器人质心之间的相对位置矢量dr=[0.3 0.5 0.6],碰撞刚度系数为3.5237×103，恢复系数为0.69.控制器仿真参数K1=diag{0.5,0.3,0.3},ρ1=5,为减少抖振，在控制器中采用饱和函数代替符号函数，饱和函数参数取为0.01.控制器仿真参数K2=diag{3,1.8,1.8},ρ2=3,η=20.

采用Matlab7.10进行仿真验证.图6为末端抓捕器对目标抓捕过程中因碰撞对基座造成的碰撞力矩，碰撞发生时间小于0.5 s，碰撞力矩最大值为7.49 N·m，仿真结果显示碰撞具有时间短，冲击力矩大的特点，在输出控制力矩有限的条件下，对控制器的设计提出了更高的要求.

图7给出了姿态偏差的欧拉角变化曲线，图8显示了角速度偏差变化曲线，采用反步积分滑模控制器对虚拟量控制，避免了传统滑模控制器直接控制状态量所产生的反应快、超调大的问题，使得基座姿态在较大力矩冲击的作用下，保持了渐进稳定，具有较强的鲁棒性，最大姿态偏差为7.054°，最大角速度偏差为0.5566(°)/s，满足抓捕过程中对基座稳定要求的性能指标.姿态偏差与角速度偏差均在150 s之后收敛到零，完成了目标抓捕后的稳定控制.

图6 碰撞力矩Fig.6 Impact torque curve

图7 姿态偏差欧拉角变化曲线Fig.7 Attitude errors with RPY parameters

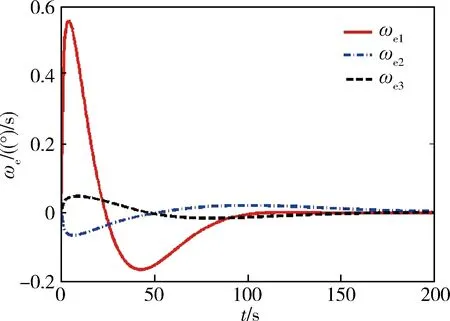
图8 角速度偏差ωe变化曲线Fig.8 Angular velocity errors curve

图9给出了控制力矩的输出特性曲线，图10显示了反作用轮的力矩输出曲线，采用饱和函数代替了符号函数，控制力矩输出平滑，具备工程可实现性.反作用轮输出力矩小于0.5289 N·m，满足最大输出力矩1 N·m的要求.力矩输出时间小于100 s，保证了系统具备一定冗余度和安全边际，提高系统的稳定度.

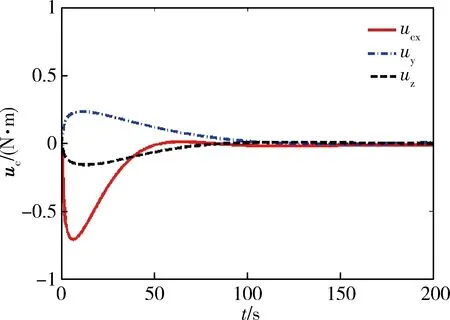
图9 控制器力矩输出曲线Fig.9 Control torques curve of combined spacecraft

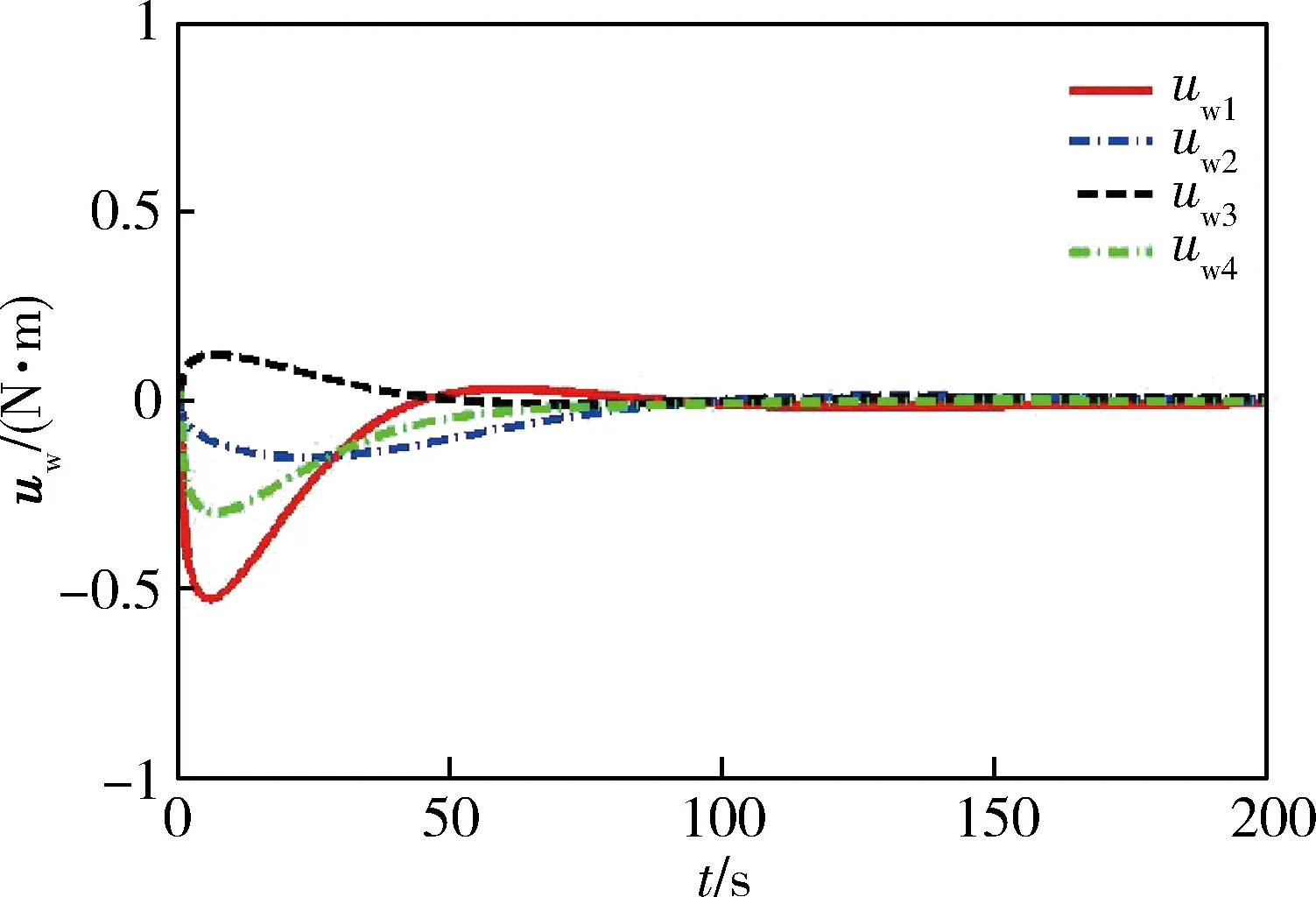
图10 反作用轮力矩输出曲线Fig.10 Control torques curve of reaction wheels

图11给出了反作用轮转速的变化曲线，通过基于伪逆的反作用轮控制力矩重分配方法，将碰撞产生的扰动力矩最优的分配到4个斜装反作用轮上，因碰撞位置的随机性导致碰撞力矩的不确定，使得反作用轮的转速不同，反作用轮最大转速为350 r/m，小于最大饱和值500 r/m，因此，利用空间机器人的4个反作用轮姿态控制系统不仅能够实现碰撞后的复合航天器稳定控制，而且由于采用了可再生能源，节约了宝贵的推进剂，增加了空间机器人的使用寿命.

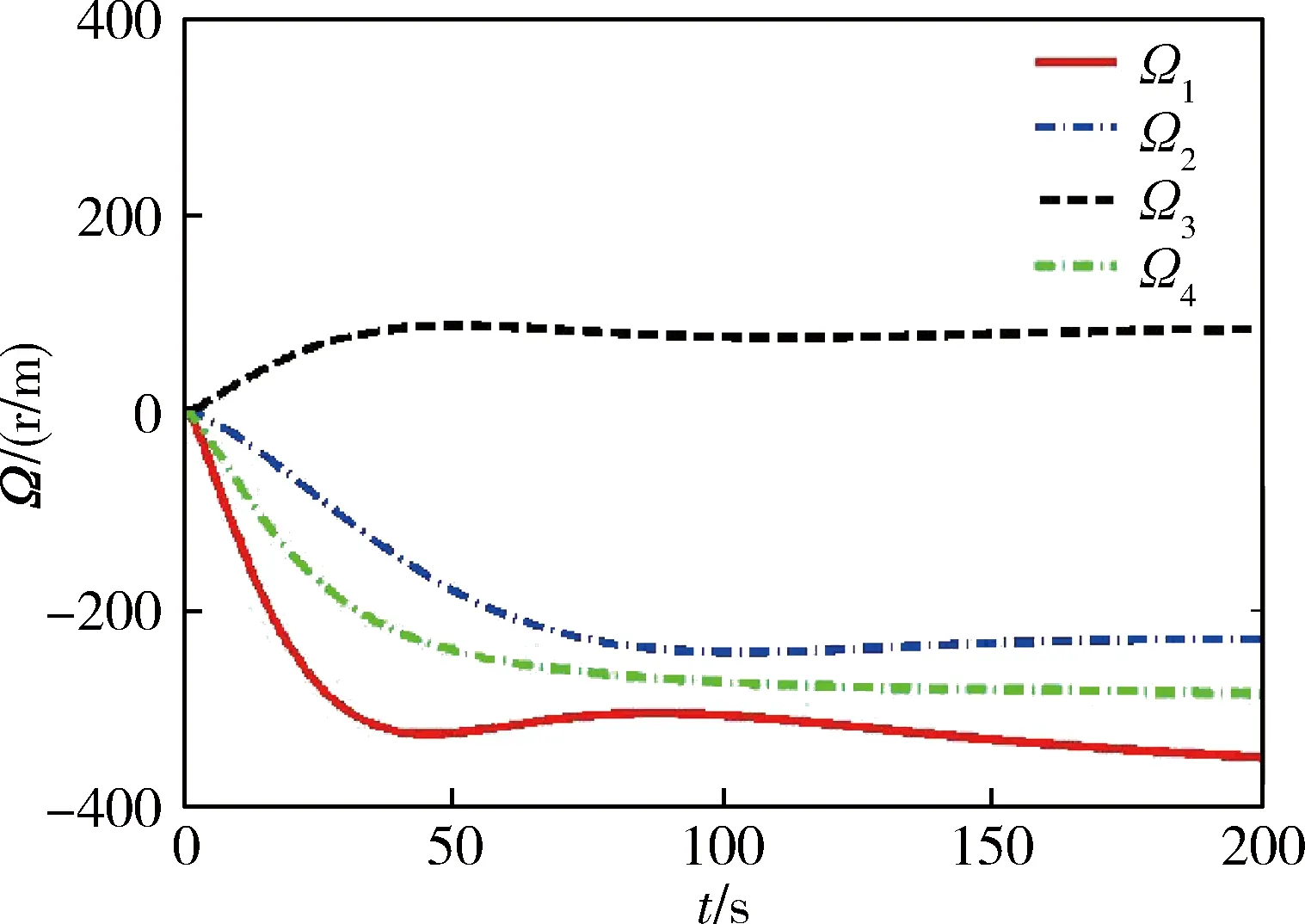
图11 反作用轮转速Ω变化曲线Fig.11 Speed curve of reaction wheels

4 结 论

针对空间目标抓捕过程中的碰撞及碰撞后复合航天器稳定控制问题，本文提出了一种基于反作用轮重配的反步积分滑模控制方法，实现了复合航天器在抓捕碰撞后的姿态稳定控制.该方法首先引入虚拟角速度控制量，避免了因碰撞力矩产生角速度突变所导致的控制力矩输出饱和问题；采用积分滑模控制增强了系统的鲁棒性，提高了系统应对参数突变的能力；将控制量分解为实现姿态角稳定的外环和实现角动量稳定的内环，改善了系统的动态特性.通过计算本体坐标系到惯量主轴坐标系变换矩阵，对空间机器人的反作用轮进行了重构，使其可以在复合航天器稳定控制中完成执行器的功能.最后，采用基于伪逆的反作用轮控制力矩重分配法，将输出的控制力矩在各个反作用轮间进行最优分配，通过作用轮吸收碰撞力矩，实现碰撞后的复合航天器的稳定控制.通过仿真证明了方法的有效性，仿真结果表明，复合航天器的姿态与角速度在有限时间收敛到了零；输出的控制力矩平滑，具备工程实用性，控制力矩小于最大输出力矩要求；反作用轮最大转速小于饱和值，具备复合航天器姿态稳定能力，同时节约了宝贵的推进剂.