基于改进蚁群算法的多机器人任务分配*

秦新立，宗 群，李晓瑜，张博渊，张秀云

0 引 言

机器人可以代替人类完成一些复杂、繁琐、危险系数较高的任务，不仅可以提高工作效率，还可以降低人类完成任务所付出的代价.虽然单个机器人的能力在不断提高，但是对于一些复杂的任务，单个机器人并不能满足人类的要求，多机器人系统成为近年来研究热点和发展方向[1].多机器人任务分配(multi-robot task allocation, MRTA)是指在机器人执行多个任务时，由于机器人性质、用途、任务载荷等各不相同，在满足各种约束条件下，为机器人找到最佳的任务分配方案，在保证机器人执行任务代价最小的情况下，能够获得最大的收益.

任务分配的方式主要有集中式分配和分布式分配.目前，针对集中式的任务分配模型主要有多维旅行商模型[2](multidimensional traveling salesman problem, MTSP)、车辆路径模型[3]、多维动态网络流优化模型[4]、多维多选择背包问题模型[5]以及相关模型的改进.针对分布式的任务分配模型主要有博弈论模型[6]，拍卖算法模型[7]等.MRTA是组合优化中典型的NP-Hard问题.解决MRTA问题主要有启发式算法和分布式拍卖算法.分布式拍卖算法主要面向任务的动态执行和自主求解，并在求解过程中考虑各平台之间的信息交互和协商[8].启发式算法存在随机性，搜寻范围广，且易于实现、计算复杂度低、求解效率较快[9].

本文采用启发式算法解决复杂约束环境下的MRTA问题.为有效解决传统蚁群算法收敛速度慢且易陷入局部极值的问题，引入遗传算法中的变异算子进行局部优化，引入改进模拟退火算法跳出局部极值.

1 问题描述

根据机器人智能自主执行任务场景，考虑机器人数目约束、电量约束以及任务载荷等约束，以性能指标最小为目标函数，构建MRTA问题描述.记机器人数量为R，任务数量为T.

1.1 约束指标

(1) 机器人数目约束

针对多机器人编队任务分配问题，为了突出多个机器人协同执行任务的特点，考虑任务目标数目远远大于机器人数目，要求每个机器人执行多个任务目标，且每个任务目标都需要被执行且只被一个机器人执行，可以表示为

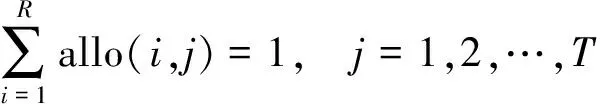
(1)

式中allo(i,j)表示第i个机器人对第j个任务的执行情况，1表示执行，0表示不执行.

(2) 电量约束

根据机器人和任务目标的位置，计算机器人各自的电量消耗.第i个机器人所在基地和第j个任务目标的距离可以表示为

(2)

式中，rx_pi,ry_pi分别表示第i个机器人在横纵坐标上的位置，tx_pj,ty_pj分别表示第j个任务在横纵坐标上的位置.第i个任务目标和第j个任务目标距离可以表示为

(3)

第i个机器人执行任务的电量消耗可以表示为

ei=r_ui×di

(4)

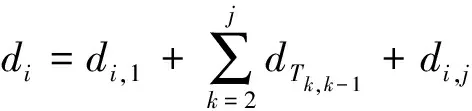
为了确保完成任务后机器人的安全，要求自身携带电量能够确保返回基地，可以表示为

ei≤r_ci

(5)

式中r_ci表示第i个机器人的电量情况.

(3) 任务载荷约束

任务载荷表示每个机器人可以执行任务数目，其约束可以表示为

(6)

1.2 性能指标

性能指标是由任务收益函数、任务代价函数和罚函数部分综合得到的：

subject to:

(7)

其中，ω1,ω2,ω3分别表示电量消耗，收益，以及罚函数的权重系数，gij表示收益函数，pe表示罚函数.罚函数构造思想主要是把有约束问题转化为无约束问题进行求解[10]，即把任务载荷约束式(6)转化为性能指标，可以表示为

(8)

2 求解算法

2.1 MTSP模型

解空间的形式可采用R+T-1维向量编码，用大于T的整数表示不同机器人编号分隔点，向量的每个元素对应的正整数表示任务编号或不同机器人编号分隔点[11].如3个机器人执行10个任务的解空间为4-7-8-11-10-1-9-3-12-2-5-6，表示机器人1顺序执行任务4、7、8；机器人2顺序执行任务10、1、9、3；机器人3顺序执行任务2、5、6.

由于每个机器人需要执行多个任务，且每个任务都需要被执行，可以把多个机器人看成多个旅行商.MRTA问题可以转化为MTSP模型.

2.2 基本蚁群算法

蚁群算法是意大利学者DORIGO[12]于20世纪90年代基于蚂蚁觅食提出的智能算法.根据蚂蚁觅食规律，建立机器人选择任务过程.机器人r执行任务i到任务j的转移概率满足：

(9)

其中，τij代表任务i和任务j之间的信息素的强度，ηij代表任务i和任务j之间的启发式因子的强度.α表示信息素重要程度，β表示启发式因子重要程度，ar表示需要被执行的任务.

迭代过程中信息素更新满足：

τij(τ+1)=(1-ρ)τij(τ)+Δτij

(10)

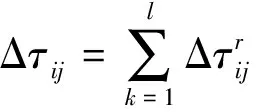
(11)

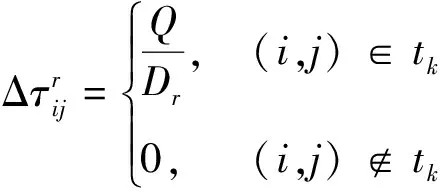
(12)

其中，ρ表示信息素蒸发系数，Q表示信息素增加强度系数，Dr表示机器人性能指标，tk表示机器人r执行过的任务.

2.3 改进蚁群算法

采用基本蚁群算法构造解空间，然后采用遗传算法中的变异算子二次优化每个机器人执行任务的顺序，并根据模拟退火过程中Metropolis准则以一定的概率接受二次优化过程的较差的解.

在模拟退火过程中，为使算法收敛速度更快，采用动态温度衰减因子.温度衰减因子与迭代次数的函数关系表示为

(13)

式中k为迭代次数，其关系曲线如图1所示.

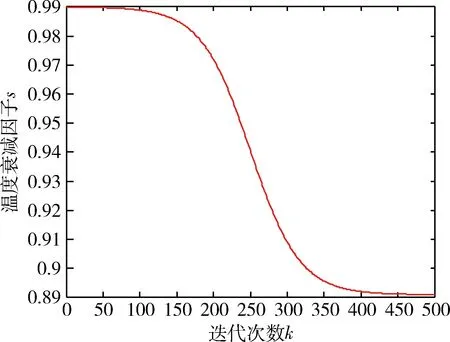
图1 温度衰减因子s与迭代次数k关系曲线Fig.1 s-k curves of specimens

改进蚁群算法基本流程如图2所示，具体如下：

步骤1：(初始化参数)设置蚁群算法、模拟退火算法的相关参数.

步骤2：(构建解空间)针对每个机器人，按照任务转移概率式(9)计算其需要执行的任务，直到所有的机器人执行完所有任务.

步骤3：(变异操作)执行变异操作时，从当前解空间中随机选择两个基因，将基因间的子序列进行倒置.

步骤4：(模拟退火准则)计算新的解的适应度值，如果优于学习前的适应度值，则接受新的解；否则按Metropolis准则判断是否接受新的解.

步骤5：(更新解空间)根据变异操作和模拟退火准则更新解空间.

步骤6：(更新信息素)计算每个机器人执行任务的收益与代价，记录当前迭代次数中最优解，同时根据式(10)对迭代过程中的信息素浓度进行更新.

步骤7：(迭代判断)判断当前迭代次数是否达到迭代阈值：如未达到，跳转到步骤2，循环执行；否则终止寻优，输出最优解.

3 仿真与分析

为验证设计优化算法的性能，在Windows10操作系统上，基于Matlab2014a环境实现算法的仿真实验.PC机配置为Intel(R) Core i5-6500@3.2GHz处理器，4 G内存.

假设某发电厂有4个清洁机器人以及40个需要清洁的太阳能电池板，即R=4，T=40.设置蚂蚁数A=10，信息素重要程度α=1，启发式因子重要程度β=5，信息素蒸发系数ρ=0.1，信息素增加强度系数Q=50，迭代阈值K=500，初始温度Te=8，静态温度衰减因子s=0.99，动态温度衰减因子取值如式(13)所示，求解适应度值权重ω1=0.5,ω2=0.5,ω3=1 000.机器人相关性能如表1所示.由于任务数目过多，相关性能不再赘述.

图2 改进蚁群算法流程图Fig.2 Flow chart of improved ant colony algorithm

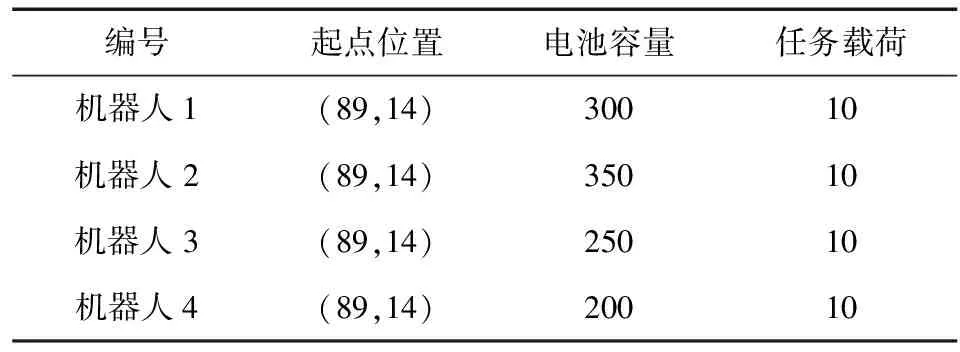
表1 机器人性能参数表Tab.1 Table of robot performance parameters

表1中，所有机器人单位电量消耗均为1，那么电池容量约束可以简化为路程约束.

如图3所示，分别给出了基本蚁群算法和改进蚁群算法求解MRTA问题的迭代过程变化曲线.

如图4所示，分别给出基本蚁群算法和改进蚁群算法求解MRTA问题进行200次蒙特卡洛仿真过程中平均性能指标情况对比.

从图3和图4可以看出，相比基本蚁群算法，改进蚁群算法性能指标更低，表明改进蚁群算法在迭代过程中有利于跳出局部最优值；且改进蚁群算法收敛速度更快，验证了算法的有效性.

MRTA优化结果如表2所示，仿真结果如图5所示，可以看出每个机器人执行10个任务，满足任务载荷约束.

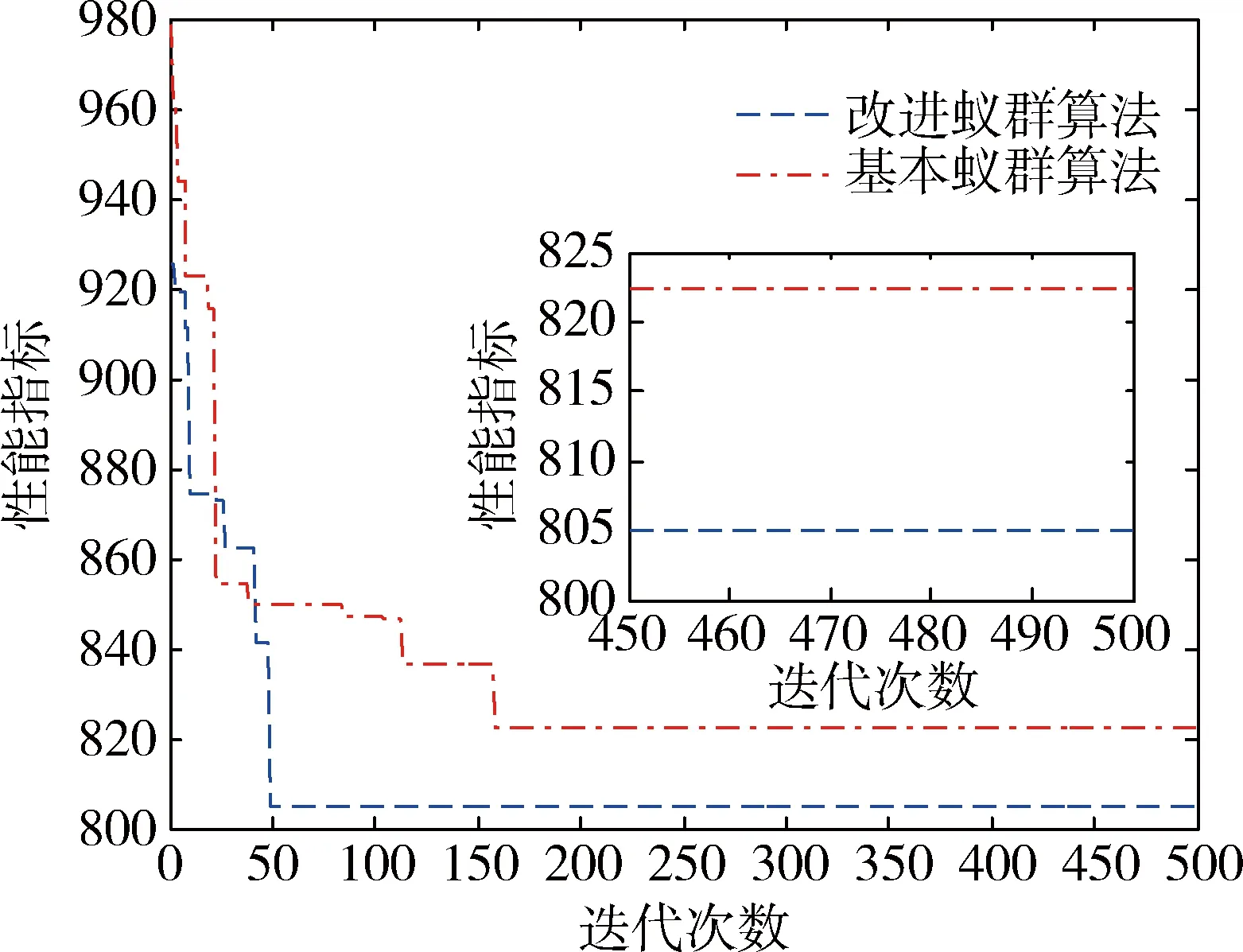
图3 基本蚁群与改进蚁群算法仿真对比Fig.3 Comparison between ant colony algorithm and the improved ant colony algorithm

图4 两种算法蒙特卡洛仿真对比Fig.4 Comparison of two kinds of Monte Carlo algorithms

表2 任务分配优化结果Tab.2 Optimization results of task allocation

图5 多机器人任务分配优化结果Fig.5 Optimization results of multi-robot task assignment

4 结 论

本文通过采用MTSP模型和改进蚁群算法，解决复杂约束下MRTA问题.针对基本蚁群算法收敛速度慢且易陷入局部最优问题，引入局部优化变异算子和改进模拟退火算法，利用变异算子进行局部优化，并采用模拟退火机制中Metropolis准则依概率接受差的解，使算法能够跳出局部极值.仿真结果表明，相比基本蚁群算法，改进蚁群算法寻优效果更好.