基于凹函数的BLDCM滑模观测器控制研究

陈 威，仇志坚

(上海大学，上海 200072)

0 引 言

无刷直流电动机(以下简称BLDCM)具有体积小、质量轻、功率密度高、控制简单等特点，其无位置传感器控制由于成本低，不受工作场合限制，现已成为BLDCM的研究热点[1-3]。

现有的研究都没有系统讨论在不同控制函数情况下的观测反电动势抖振，为了定量分析反电动势的抖振，首先对已有的控制函数进行了归纳分析，提出了一种凹控制函数，并理论证明了采用凹控制函数比已有的控制函数得到的观测反电动势抖振更小。其次，将该凹控制函数作为滑模观测器中的控制函数，并用归一化方法处理估算反电动势，利用锁相环提取转速和转角信息，构建了BLDCM的无位置传感器控制系统。

1 BLDCM数学模型

两相静止坐标系下的BLDCM的数学模型如下：

(1)

式中：uα,uβ,iα,iβ,eα,eβ分别为α,β坐标系下的绕组电压、电流和反电动势；L1为每相定子绕组的等效电感；R为定子电阻。

取式(1)中的定子绕组电流和反电动势作为系统的状态变量，将绕组电压和绕组电流分别作为系统的输入和输出，并考虑到在电机控制系统中，采用周期远远小于电机的机械和电磁时间常数，可认为在采用过程中电机角速度不变，反电动势的导数为零，则由式(1)可得BLDCM的状态方程和输出方程：

(2)

y=C[ie]

(3)

2 BLDCM无位置传感器控制

2.1 反电动势滑模观测器设计

在电机运行时，若忽略电枢反应影响，可认为电机绕组电感值不变，则由式(2)构建的反电动势滑模观测器方程如下：

(4)

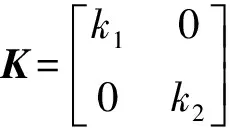
选择滑模面：

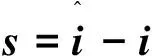
(5)

将式(4)减去式(2)，可得滑模观测器的误差方程：

(6)

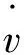
(7)

对式(7)求导，得其导数：

(8)

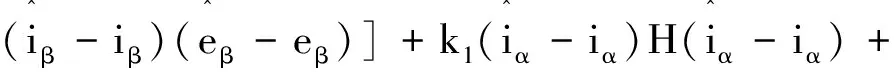
(9)

由于在滑模观测器中，选用的控制函数值域为[-1 1]，且H(x)与x符号相同，结合不等式的性质可得：

故只需式(10)小于0，就能保证滑模观测器进入滑模面，即：

(11)

(12)

将式(12)代入式(6)，得：

(13)

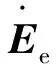
(14)

为求得g1,g2的范围，重新构造一个Lyapunov方程：

(15)

对式(15)求导，并将式(13)代入，可得：

(16)

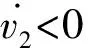
(17)

从式(11)、式(17)可知，只需选择合适的k1,k2,g1,g2参数，就能保证滑模观测器的观测值收敛到实际值。图1为滑模观测器的结构框图。

图1 滑模观测器结构框图

2.2 不同控制函数的抖振分析

(a) 符号函数

(b) e的指数函数

(c) 饱和函数

(d) 正弦函数

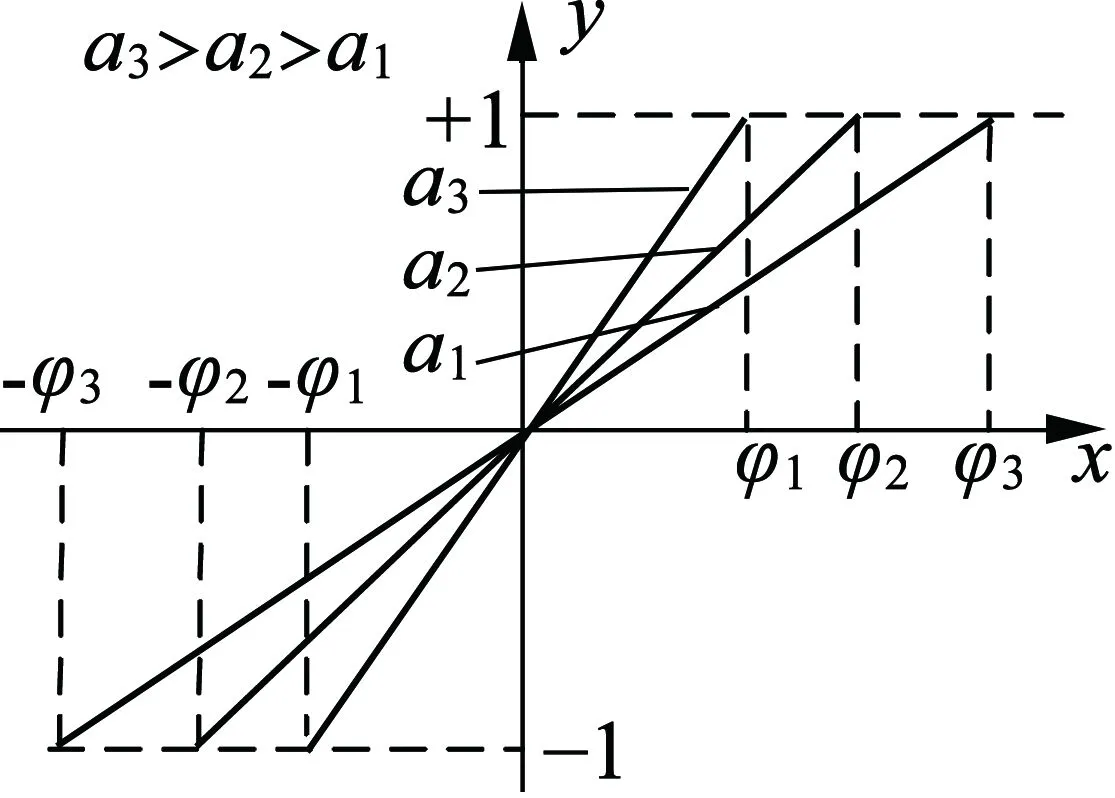
已有的控制函数可以分为符号函数，e的指数函数，饱和函数，正弦函数，曲线如图2所示。数学表达式如下：

(18)

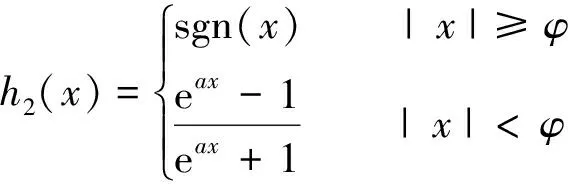
(19)

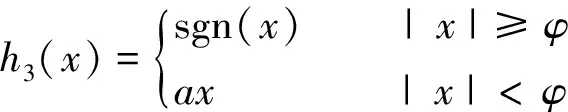
(20)

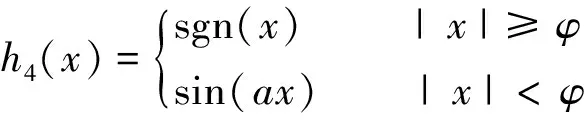
(21)

式(19)中，当a分别取1,2时，即为sigmoid函数和双曲正切函数tanh。

图3 凹、凸控制函数

观察图2的函数图像可得，当a越大时，在边界层内控制函数的坡度越陡，越接近符号函数，抖振越大。分别对上述函数求其一阶、二阶导数，由高等数学中函数凹凸性定义可知，e的指数函数和正弦函数在边界层内为凸函数。本文现提出一种凹控制函数，该凹控制函数与其凸控制函数关于y=ax对称，具体图形如图3所示。现定量地推导凹、凸控制函数的反电动势抖振数学表达式，为叙述方便，凹、凸控制函数分别记为hm(x)与ht(x)，定义反电动势的抖振：

(22)

依式(22)可计算得到，分别采用凸、凹控制函数作为滑模观测器的控制函数情况下，反电动抖振分别如下：

(23)

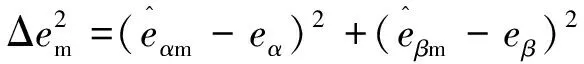
(24)

式中：下角标t，m分别表示凸、凹控制函数的变量。将式(23)与式(24)作差，得到：

根据式(14)，且依据在边界层内，滑模观测器中的控制函数过零点，可计算得到：

(26)

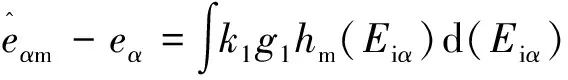
(27)

将式(26)、式(27)分别作差、相加，可分别得到：

(28)

(29)

由于在边界层内h(x)与x同号，且|ht(Ei)|大于|hm(Ei)|，因此式(28)、式(29)都大于0。而β方向的变量与α方向变量具有相同的性质，因此也可得到：

将上式代入式(25)，得到：

(30)

故在边界层内对于任意的Ei，都恒有Δet大于Δem成立。因此，在其他条件相同的情况下，选用凹控制函数，能降低观测反电动势的抖振。

本文以正弦函数为例，其数学表达式见式(21)，其中将其凹切换函数记为g4(x)，根据曲线f(x,y)=0关于直线y=kx+b对称的曲线方程：

可求得正弦函数h4(x)关于y=ax对称的凹控制函数g4(x)应满足：

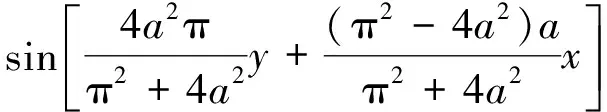
(31)

式(31)是隐函数，无法直接求得解析解，现考虑sin(ax)的麦克劳林展开式，并忽略高次项，运用MATLAB软件，解出显函数表达式。

2.3 反电动势归一化处理和转子速度及转角计算

由于BLDCM的气隙磁场为梯形波，a,b,c坐标系下的反电动势变换到α,β坐标系下也不是正弦波，若直接用该反电动势提取转子位置角和转速信息，误差较大，计算精度不高。为此，采用式(32)对滑模观测器的观测反电动势进行归一化处理[10]，以降低其中的高次谐波含量，并消除磁链和角速度的影响，获取类似于正弦波形的基波信号。

(32)

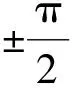
图4 锁相环原理框图

由图4可知：

(33)

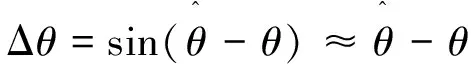
(34)

2.4 BLDCM的无位置传感器控制系统

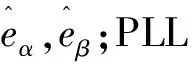
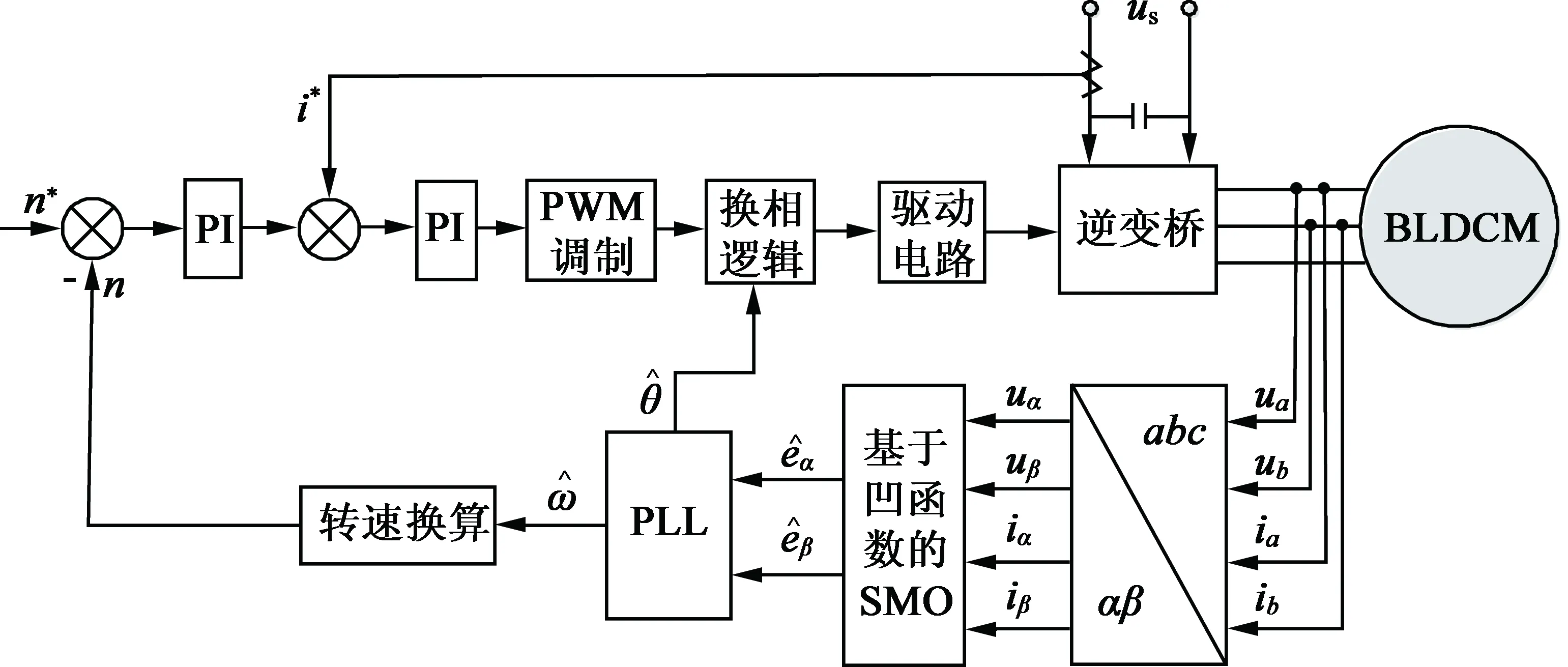
图5 BLDCM无位置控制框图

3 仿真分析

3.1 BLDCM无位置传感器控制系统

基于以上分析，根据图5在 MATLAB/Simulink搭建控制系统，滑模观测器的参数k1=-700000，k2=-600 000，g1=-0.330 545，g2=-0.090 01，电机的参数如表1所示。

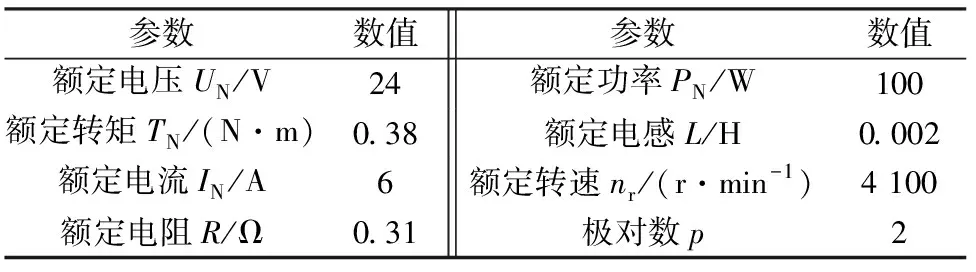
表1 仿真电机参数

3.2 凹、凸控制函数的反电动势抖振对比分析

在反电动势抖振对比分析中，转速环、电流环的PI调节器参数和滑模观测器的k1,k2,g1,g1数值相同，只有控制函数不同。其中，凸控制函数选用正弦函数，其数学表达式见式(21)，它关于y=ax对称的凹控制函数g4(x)如式(31)所示，结合sin(ax)的麦克劳林展开式，忽略高次项，运用MATLAB软件，解出其数学表达式，其中a均取0.785，φ均取2。

图6(a)为电机空载情况下，给定转速4100r/min，采用凹、凸控制函数下的反电动势抖振波形。当电机稳定在额定转速，在t=0.6 s时刻，突加0.38 N·m的额定负载，此时基于不同控制函数下的反电动势抖振波形如图6(b)所示。对图6分析可得，加载前后，采用凹、凸控制函数，观测的反电动势都是有抖振的，但是采用凹控制函数的反电动势抖振是明显减小的，这也证明了前文分析的正确性。

(a) 空载时，凸、凹控制函数下的反电动势抖振

(b)加载时，凸、凹控制函数下的反电动势抖振

3.3 基于凹控制函数的滑模观测器的仿真结果

基于前面所述的凹控制函数建立BLDCM无位置传感器控制系统，电机在α，β轴下的反电动势、转子位置角和转速的波形如图7～图13所示，其中t=0.6 s时刻，突加0.38 N·m的额定负载。

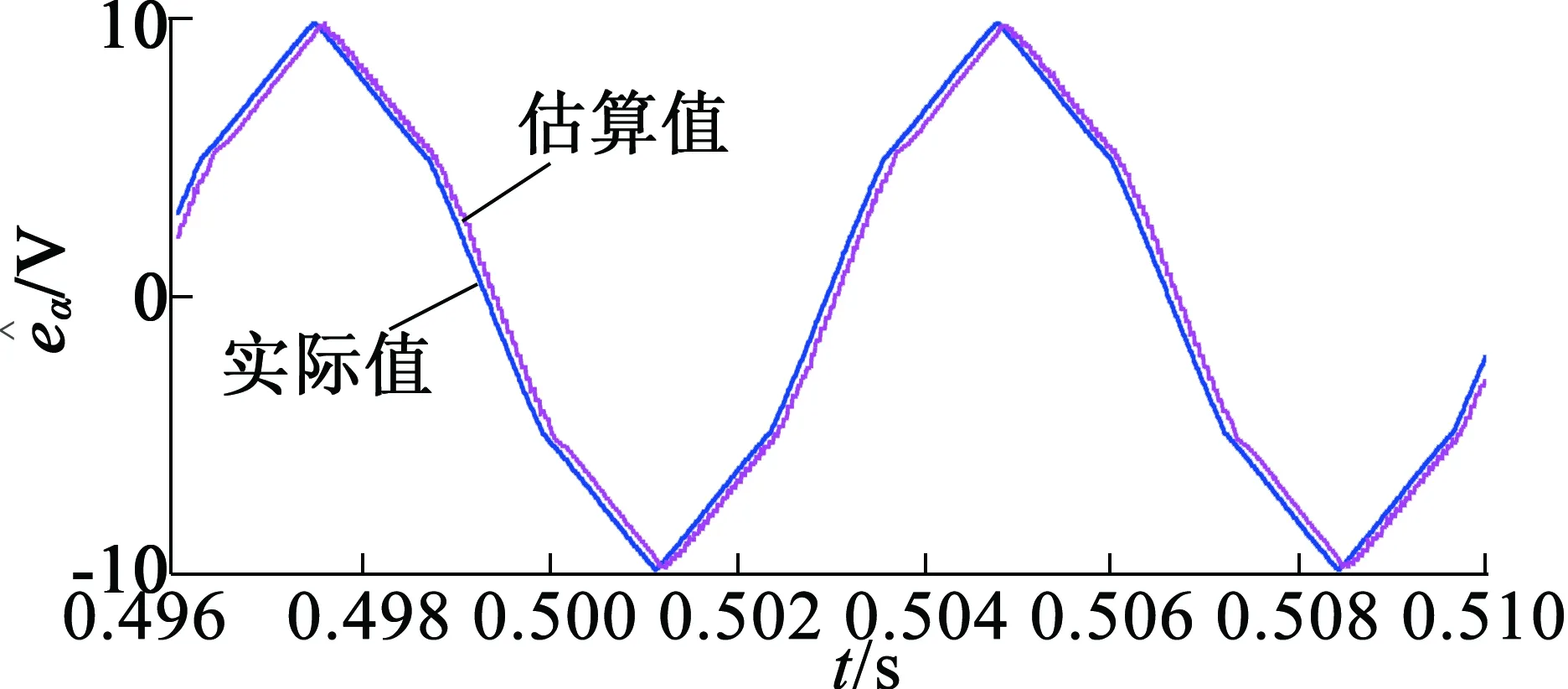
图7 空载情况下，

波形

图8 加载情况下，

波形

图9 空载情况下，

波形

图10 加载情况下，

波形

图11 空载情况下，转子位置角θ波形

图12 加载情况下，转子位置角θ波形

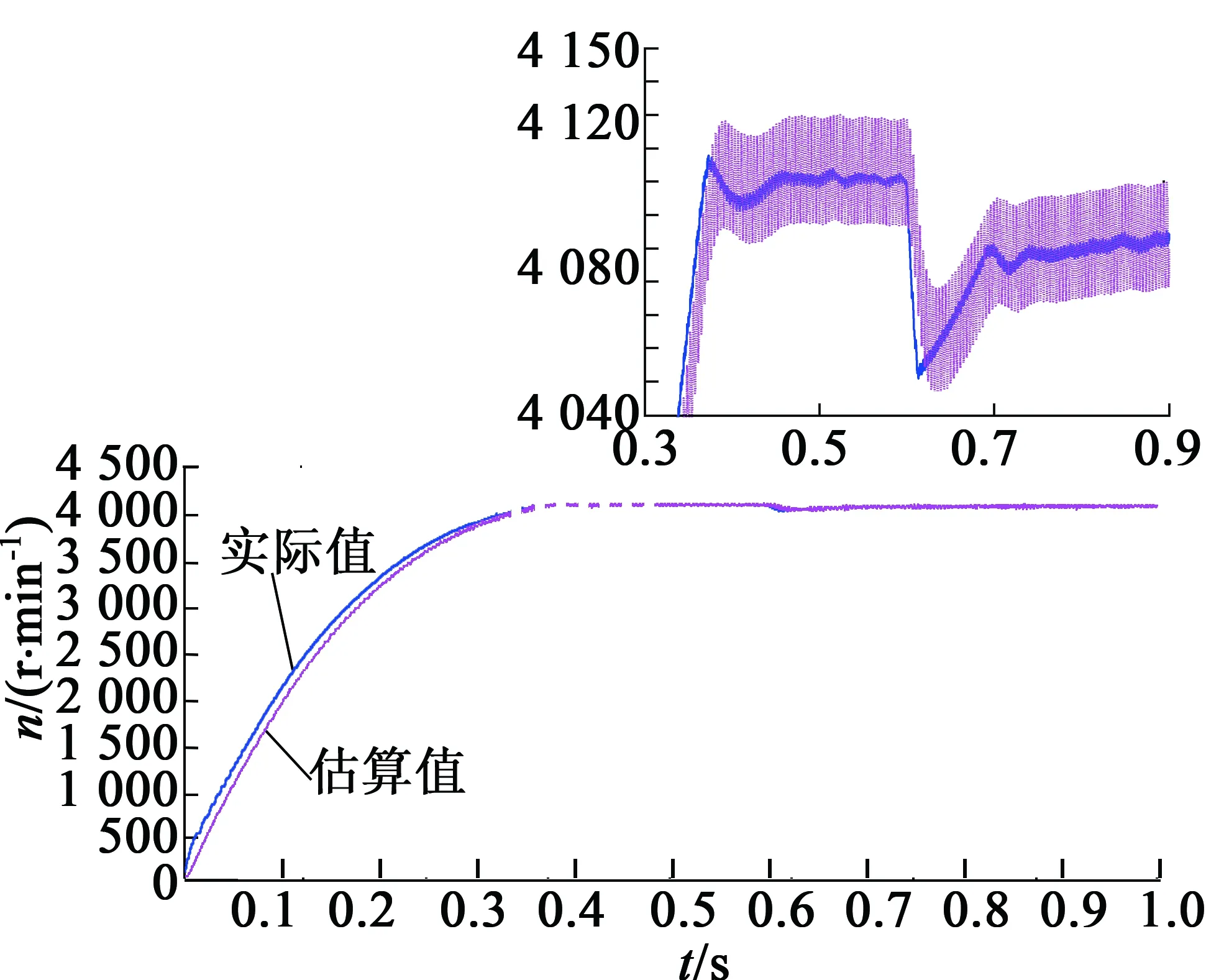
图13 空载和加载情况下的转速波形

对上面各图分析可知，基于凹控制函数作为滑模观测器中的控制函数，不管是在空载还是在突加负载情况下，反电动势和转子位置角估算值都是可以跟随实际值的，反电动势没有出现明显的抖振，电机转速也比较平稳，加载前后只有十几转速差，转子位置角约有3°差值，没有出现大的相移。本文的方法是正确有效的，能削弱反电动势抖振和提高转子位置角精度。

4 结 语

本文从函数的凹凸性角度分析了已有的控制函数，提出了一种凹控制函数，并将其应用到滑模观测器中作为控制函数，并理论证明了基于凹控制函数的滑模观测器中的反电动势抖振明显小于采用凸控制函数的，是可以削弱抖振的。仿真结果表明，在负载以及转速突变的情况下，本文方法都能准确得到平滑的反电动势，及时跟踪电机的转速和转角变化，具有较好的稳态精度和良好的控制性能。