水面稳定平台干扰补偿技术研究

徐伊岑，李坤龙，商 飞

(1.无锡商业职业技术学院，无锡 214153；2.南京理工大学，南京 210094)

0 引 言

稳定平台是一种主动式隔离设备，可以安装在多种运动载体上，隔离姿态扰动，给平台上被控对象提供一个稳定基准面[1-3]。稳定平台在军事、民用、工业上得到了广泛应用。本文以某型水面稳定平台为研究对象，其上设备在跟随水面载体运动过程中受到多种干扰的影响。稳定平台在工作过程中除要隔离载体的姿态扰动，还会受到摩擦、抖动及传感器测量噪声等的干扰。在众多干扰中，载体姿态扰动、系统摩擦力矩干扰、平台定位抖动干扰对稳定平台影响较大，因此，研究稳定平台的干扰补偿技术对于提高稳定平台控制精度和稳定性具有重要意义。

由于扰动观测器(以下简称DOB)结构简单，不需要额外增加传感器，补偿范围广、使用灵活等特点，近些年来它在伺服控制系统及其他非线性控制系统摩擦等扰动补偿中的应用范围较广[4-5]。文献[6]将DOB应用在电液压力控制系统中，将非线性摩擦干扰与线性扰动分开考虑，使用DOB抑制线性扰动，并在不同速度阈值下选取不同观测值的计算方法；文献[7]在两连杆机械臂轨迹跟踪控制中设计由非线性控制器、速度观测器和扰动观测器组成的复合控制器结构，双观测器结构减少了相关传感器的使用，并抑制了摩擦等外部扰动；文献[8]提出一种基于降阶观测器的线性控制方法，用在球板系统摩擦补偿方案中，补偿低速下的摩擦干扰并抑制了极限环的产生。

加减速控制常应用在运动控制系统中，目前常用的加减速控制方法有直线加减速、指数加减速、S型加减速、三角函数加减速、多项式加减速、数字卷积加减速等[9]。S型加减速是目前使用较多的一种速度规划控制方式，具有加速度连续可导，控制平稳精确等优点。李哲等[10]将S型曲线加减速控制用于3D打印机步进电动机速度规划中，增强了系统柔性，提高了打印质量；罗申等[11]将S型加减速控制应用到狭缝涂布设备运动控制中，提升了涂布品质。

为补偿系统摩擦力矩等干扰，本文改进了经典DOB估计摩擦等干扰力矩；为抑制平台定位抖动，使用速度规划算法控制平台运动速度，并引入S型加减速控制算法。仿真及实物实验表明，控制器加入该改进型DOB和速度规划算法能够明显增强稳定平台系统的抗干扰能力，提高系统的控制稳定性和精度。

1 水面稳定平台伺服控制系统模型分析

假设系统已通过合适的方法消除了机械谐振等造成的影响，仅考虑摩擦力矩和传感器测量噪声干扰时稳定平台单轴速度环控制结构，如图1所示。

图1 单轴速度环控制结构

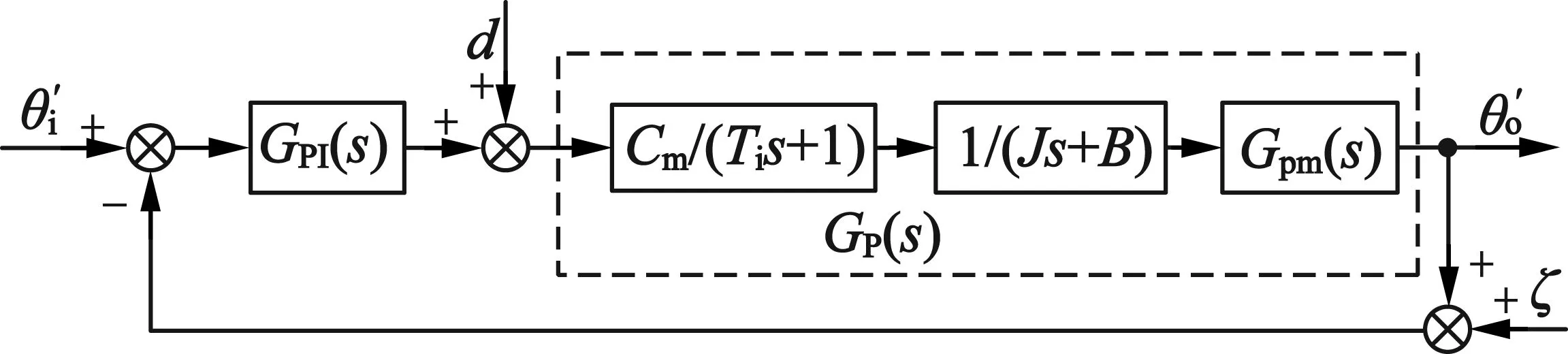
图2 简化的单轴速度环控制结构

图2中，d为等效外部扰动；Ti为电流环时间常数；Gp(s)为等效控制对象。

2 稳定平台干扰补偿技术

2.1 基于经典DOB的稳定平台控制系统

为方便问题分析及仿真验证算法的有效性，本文引入经典LuGre动态摩擦模型，该模型能够模拟出稳定平台低速运行时由摩擦干扰引起的滞-滑特性。将摩擦模型输出作为等效干扰d，设计基于经典DOB的稳定平台速度环控制结构如图3所示。

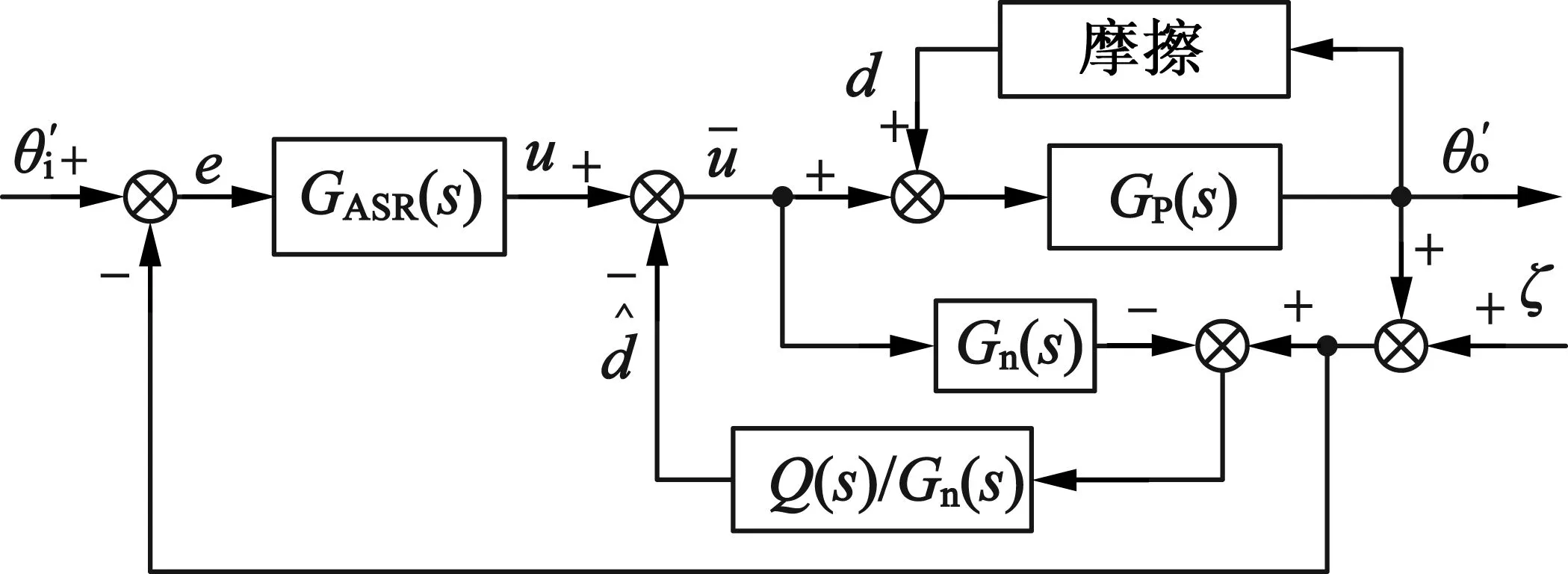
图3 基于经典DOB的速度环控制结构

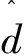
根据叠加原理，当同时存在参考输入(ω2,)，摩擦干扰d和传感器测量噪声ζ时，被控对象输出对参考输入摩擦干扰d和传感器测量噪声ζ的传递函数：

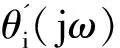
假设2 假设低通滤波器Q(jω)满足：在低频段(0,ω1)，有Q(jω)≈1；在高频段(ω2,∞)，有Q(jω)≈0。

根据以上假设[14],式(1)可近似简化：

(2)

根据式(2)可以看出，基于经典DOB设计的控制器结构能够较好地抑制摩擦干扰d对系统输出的影响，但对传感器高频测量噪声和控制对象模型摄动的抑制效果并不理想。

2.2 基于改进型DOB的稳定平台控制系统

若对系统高频测量噪声不予处理，控制器在提高指令跟踪精度时，噪声会以相同精度传至系统输出[15]，极有可能引起系统的不稳定。为改善图3中控制器对高频测量噪声的抑制性能，在反馈通道中引入另一信号f补偿系统输出反馈，基于改进型扰动观测器的速度环控制结构如图4所示。

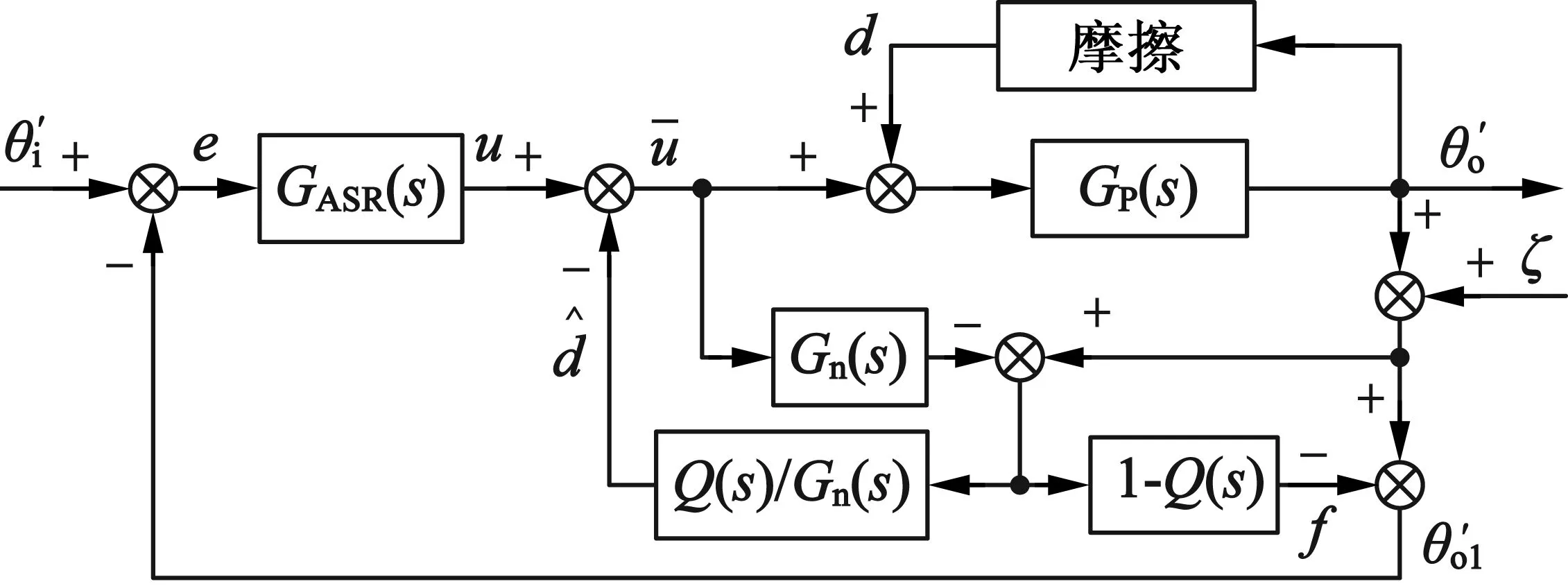
图4 基于改进型DOB的速度环控制结构

根据前面2个假设条件，式(3)可近似简化：

(4)

由式(4)可知，通过引入控制信号f，使用改进型DOB的控制结构明显提高了系统抑制高频测量噪声的能力。

此外，根据图4可得：

(5)

将式(5)等效变换，得：

(6)

由式(6)可得:

(7)

(8)

由式(8)可知，无论被控系统是否存在模型摄动和外部扰动，控制器GASR(s)输出始终与它在标称系统下一致，不受模型摄动、测量噪声的影响。

2.2.1 系统鲁棒稳定性分析

如图5所示，假定实际被控对象传递函数存在加性摄动，则控制对象实际模型与名义模型的关系可以表述:

Gp(s)=Gn(s)+W1Δ(s) ‖Δ(s)‖<1

(9)

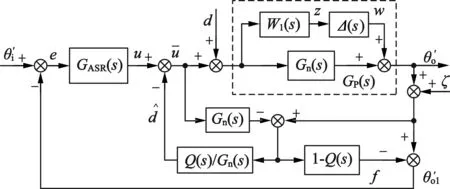
图5 加性摄动的速度环控制结构

式中：Δ(s)，Gn(s)为严格有理稳定函数；W1(s)为有界稳定的加权函数，当无外部输入信号时，从w到z的传递函数：

(10)

(11)

则w到z的传递函数的范数:

‖Gzw(s)‖

(12)

根据小增益原理，系统能够鲁棒稳定的充要条件:

(13)

因此，设计低通滤波器Q(s)时，要使其能够满足式(13)的条件。

2.2.2 系统内部稳定性分析

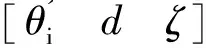
(14)

式中：Gn(s)∈H。GASR(s)能够稳定地控制Gn(s)，只需要保证是稳定的，则系统能够实现内部稳定。

2.2.3 低通滤波器设计

由前文可知，Q(s)的设计是DOB设计中的一个重要环节，直接关系到系统内部稳定性及系统鲁棒稳定性。本文使用H.S.Lee提出的二项式滤波器[16]，具体形式:

(15)

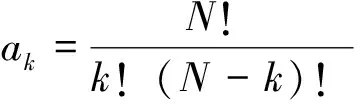
(16)

为满足系统需要，设计滤波器时间常数τ远小于系统时间常数，以实现滤波器带宽远大于系统带宽。

2.3 稳定平台抖动抑制

为抑制稳定平台定位抖动，提高系统响应性，稳定平台采用速度控制方式，依据姿态位置采用线性关系对执行机构运行速度规划，并在加减速过程中使用S型加减速曲线，实现稳定平台运行速度的平滑过渡。姿态与速度的数学关系如下：

ω=Kθ

(17)

式中:θ为稳定平台台面的实时姿态位置；ω为执行机构的实时指令速度；K为比例系数。

鉴于稳定平台对运行稳定性的需求，选取S型加减速作为稳定平台加减速控制算法。S型加减速加速及减速过程中的加速度和速度曲线如图6所示。

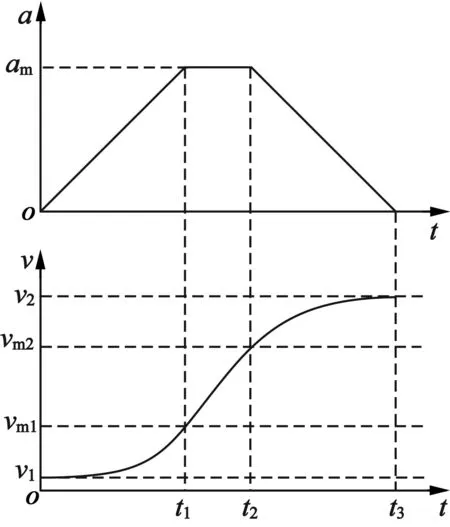
(a) 加速

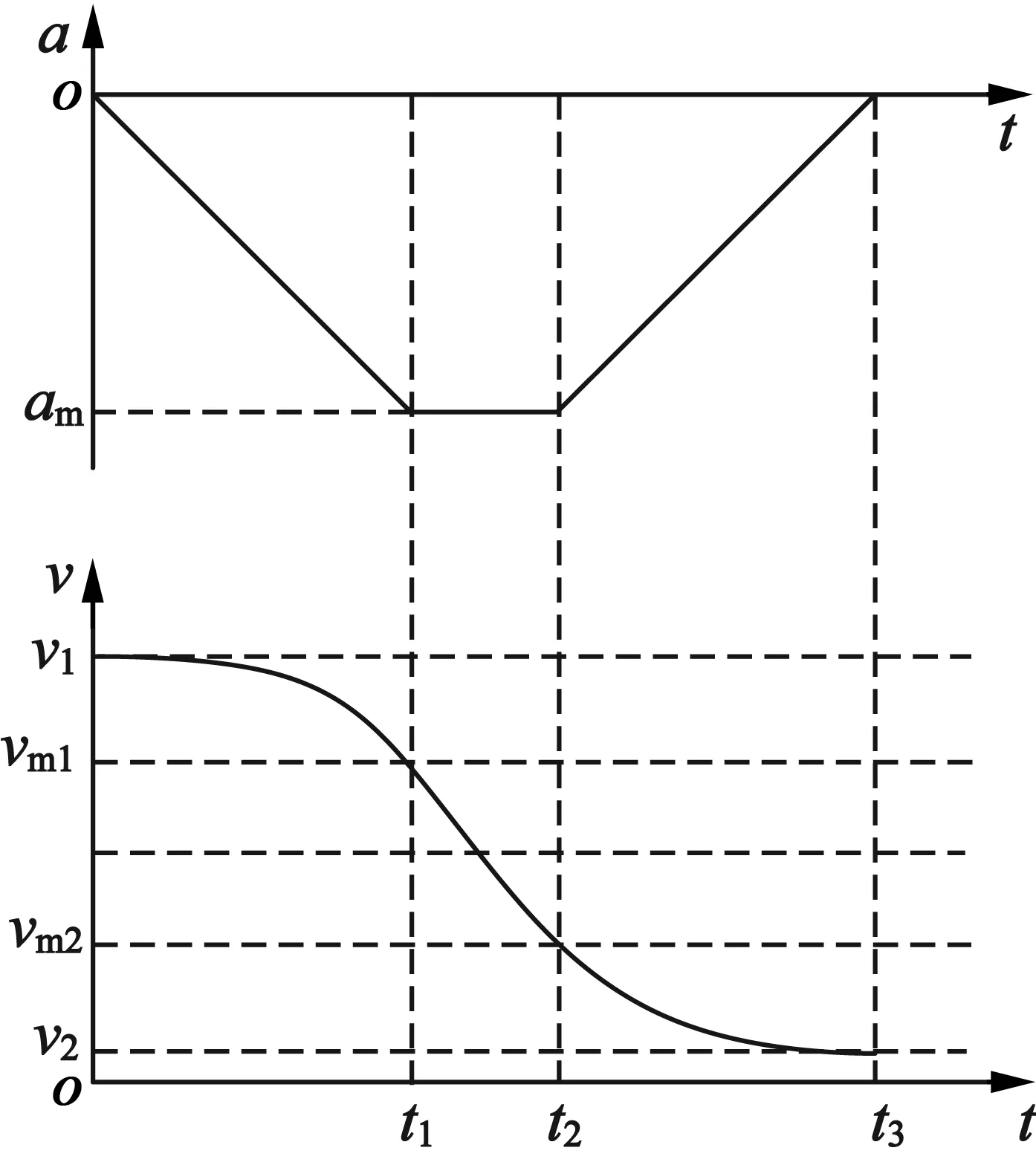
(b) 减速

由图6可知，加速度方程:

(18)

速度方程:

(19)

其中：

(20)

S型加减速是一种具有较高柔性的加减速控制方法[17]，一般可以将加速过程分为3个阶段：加加速，匀加速和减加速。这样保证了加速度的连续性及速度的平滑性。

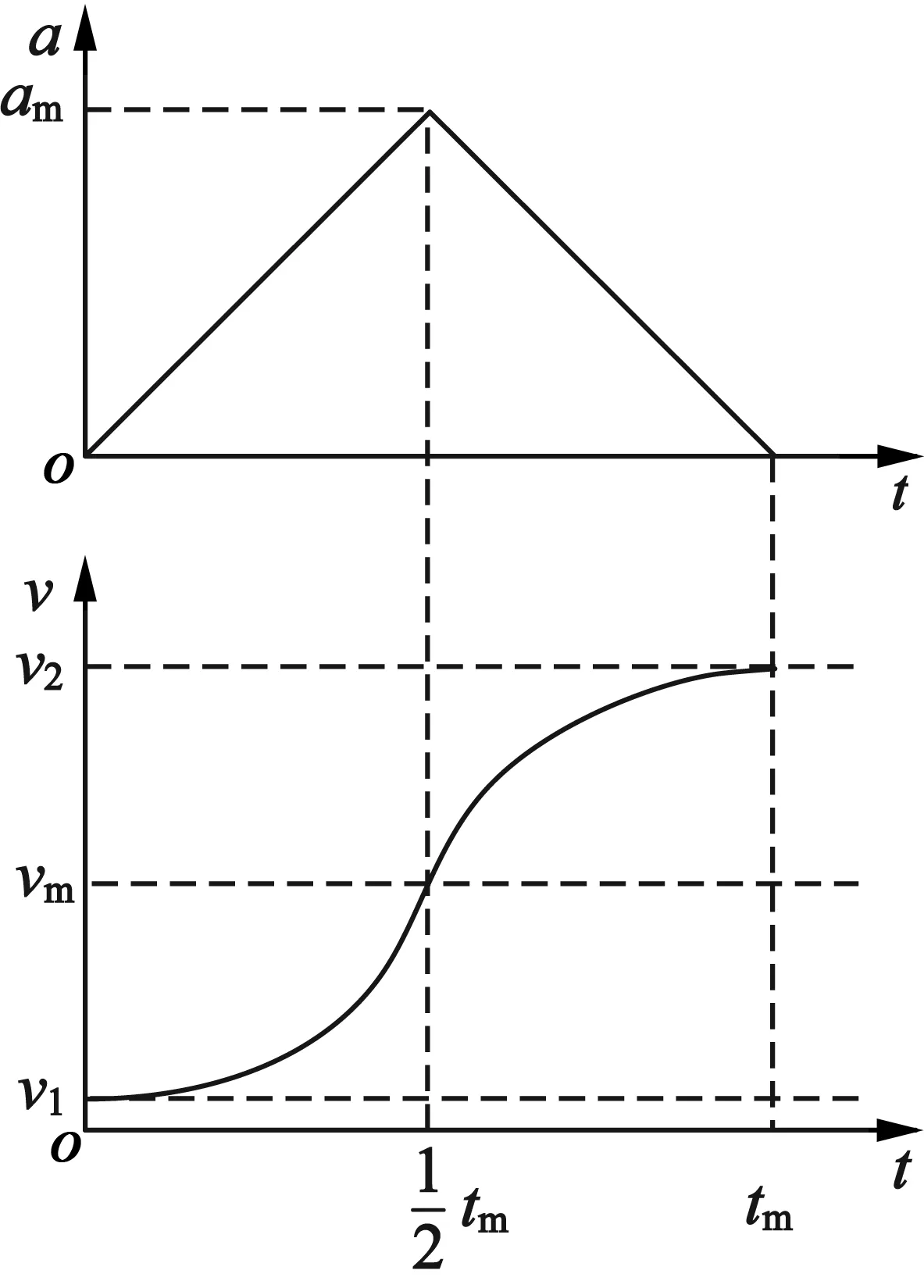
(a) 加速

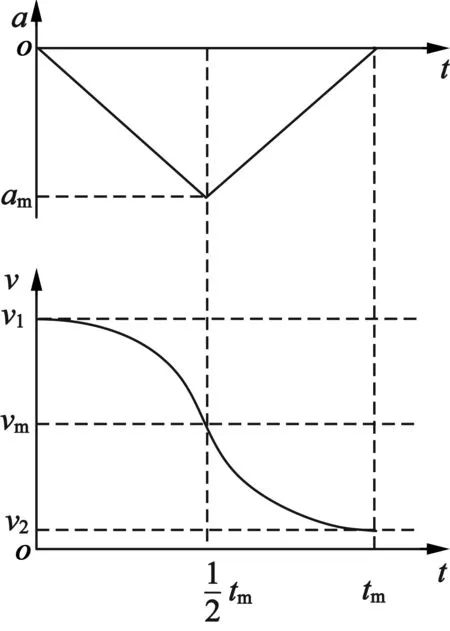
(b) 减速

加速度方程:

(21)

速度方程:

(22)

其中:

(23)

由式(23)可得:

(24)

由式(24)可知，已知起始速度、终止速度及加速或减速时间，可以求得加速度的斜率。因此，设计S型加减速参数时可以只设计起始速度、终止速度和加减速时间3个参数，较大程度上减小了计算量。

3 数值仿真实验

3.1 LuGre摩擦模型

稳定平台在工作过程中要受到摩擦力矩扰动，为模拟出稳定平台运动过程中受到的摩擦力矩干扰，选用的摩擦模型要能够反映出摩擦存在情况下平台的运动特性，特别是低速运行时的滞-滑现象[18]。LuGre动态摩擦模型能够较为精确地描述出摩擦力的动静态特性及Stribeck现象，是一个比较完善的摩擦模型[19-24]。该模型的表达式:

(25)

式中:z为接触面鬃毛平均形变；F为摩擦力；σ0，σ1为动态摩擦参数；Fc为库伦摩擦力；Fs为最大静摩擦力；α为粘性摩擦系数；Vs为切换速度。

3.2 系统数值仿真实验

以某型稳定平台伺服控制系统为研究背景，稳定平台单轴姿态调整范围为-16°～16°，此范围内，电机转动位置与平台末端运动位置为近似线性关系。为简化分析，拟合稳定平台的机械传动函数，拉氏变换得到的Gpm(s)即为机械传动传递函数，处理后Gpm(s)≈0.671，残差模|δ|≈0.011。

系统控制对象传递函数:

(26)

式中：Cm=1.03 N·m/A；Ti=7.646×10-7s；J=7.65×10-3kg·m2；B为阻尼系数，暂时忽略。根据系统速度环带宽需求，选取低通滤波器的时间常数τ=0.001 s。

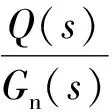
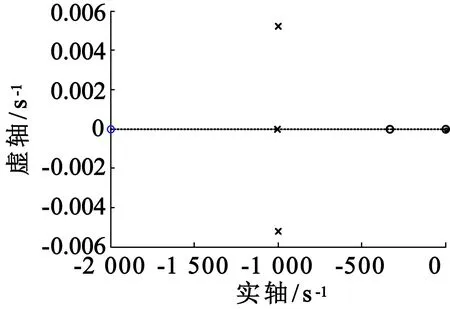
图8 零极点图

引入经典LuGre摩擦模型模拟平台所受摩擦力矩扰动，使用经典DOB和改进型DOB对摩擦干扰的估计效果如图9和图10所示(图中将摩擦力矩干扰等效到d轴电流干扰)。

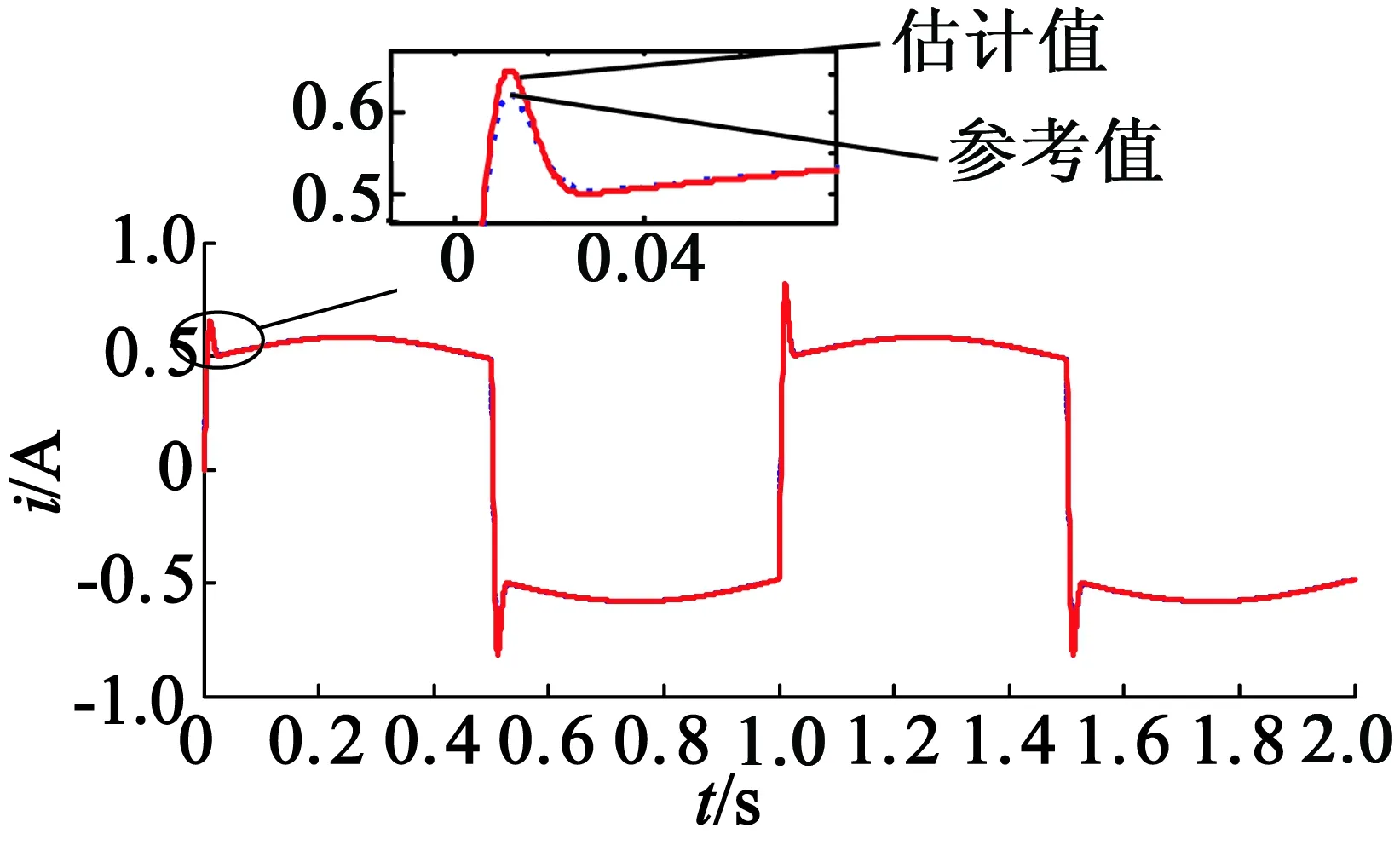
图9 使用经典DOB的摩擦估计

图10 使用改进型DOB的摩擦估计

从图9和图10摩擦观测仿真曲线可以看出，LuGre摩擦模型可以直观描述出摩擦的动静态特性，系统通过引入DOB可以较好地估计摩擦干扰的大小。

给定幅值为5 (°)/s，频率为1 Hz的正弦信号作为速度输入信号；幅值为0.02 (°)/s频率为3 000 Hz的正弦信号作为传感器高频测量噪声信号，在控制器采用单一PI控制、PI加DOB控制、PI加改进DOB控制的正弦速度跟踪效果如图11所示。只使用PI控制时，跟踪速度在给定速度上下波动范围为-0.011～0.025 (°)/s；使用经典DOB后，速度波动范围为-0.018～0.018 (°)/s；使用改进型DOB后，速度波动范围为-0.001 5～0.001 5 (°)/s。

图11 正弦速度跟踪

使用上述相同的扰动信号，速度指令以5 (°)/s2的加速度从0加速到6 (°)/s，速度跟踪效果如图12所示。只使用PI控制时跟踪速度在给定速度上下波动范围为-0.012～0.025 (°)/s；使用经典DOB后，速度波动范围为-0.017～0.017 (°)/s；使用改进型DOB后，速度波动范围为-0.001～0.001 (°)/s。

图12 加速速度跟踪

由图11和图12可以看出，单纯使用PI控制器，对摩擦干扰有一定的抑制作用，但速度跟随特性较差；引入经典DOB后速度跟随效果变好，但跟随速度以高频扰动频率和近似幅值在给定速度曲线上下波动，不能抑制高频扰动；加入改进型DOB，系统能够较好地抑制摩擦干扰和高频测量噪声干扰，速度波动范围相较于使用单一的PI控制或使用经典DOB减小近10倍。

3.3 半实物仿真实验

为验证算法的有效性，搭建半实物仿真系统，半实物仿真系统硬件组成框图如图13所示。其中，伺服原型驱动系统软件程序基于LabVIEW环境搭建，通过个人PC部署到下位机实时系统中运行；NI-RIO7842板卡板载FPGA，运行电流环控制程序及信号采集程序；电机功率驱动板主要完成电机驱动和信号调理；伺服陪测驱动系统主要完成加载。

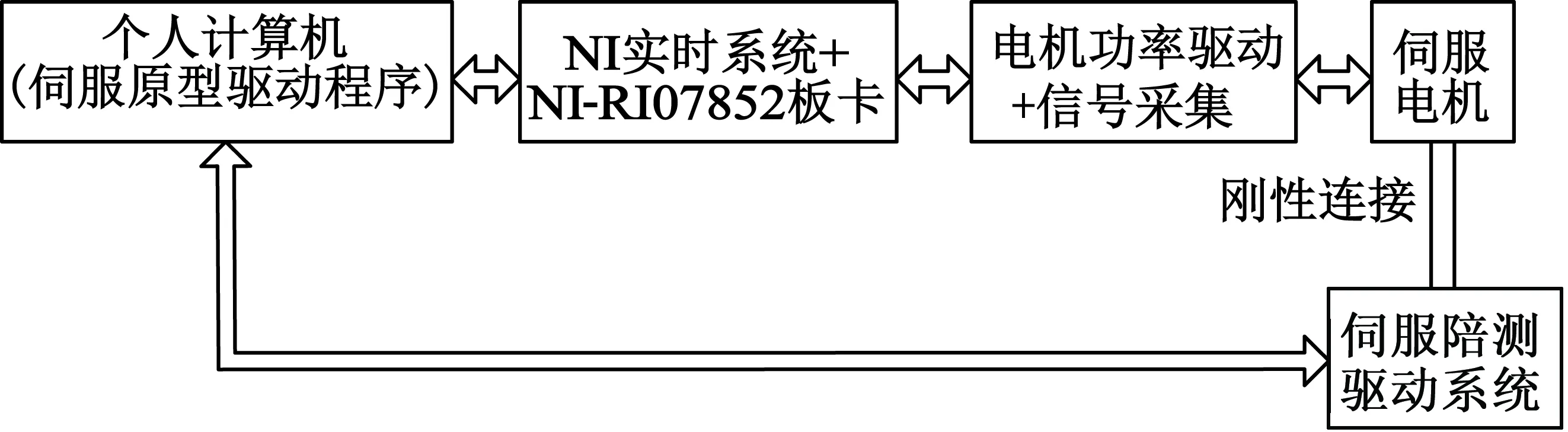
图13 半实物仿真硬件框图

执行电机与被测电机使用相同型号，电机主要参数如表1所示。

表1 电机主要参数

3.3.1 带惯量盘仿真

实际系统负载惯量比较大，实测负载惯量值约为电机转子惯量的13.2倍，半实物仿真实验中使用15倍转子惯量盘作为负载，给定周期为0.6 s，幅值为300 r/min的正弦信号作为指令速度信号。

速度为300 r/min,使用PI、PI加经典DOB和PI加改进型DOB作为控制器的速度跟踪效果如图14所示，速度跟踪偏差对比如图15所示。

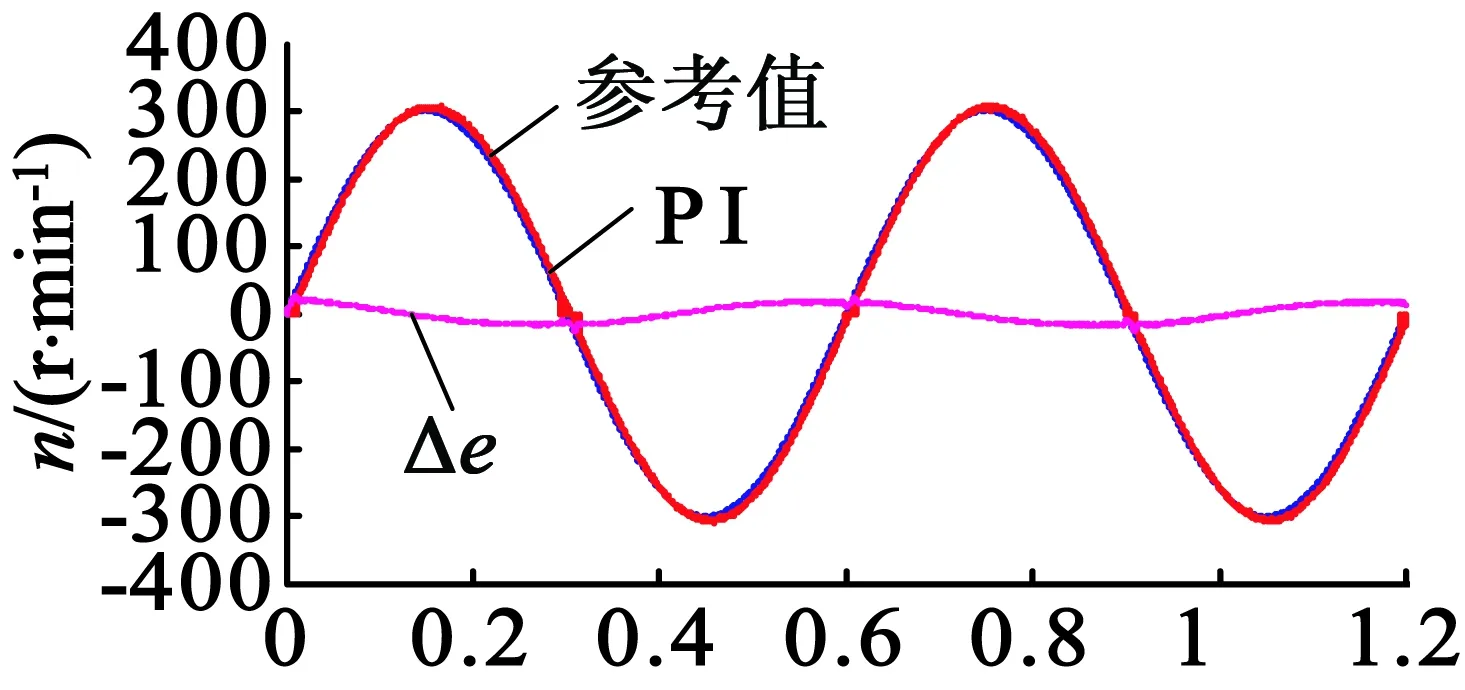
(a) 使用PI

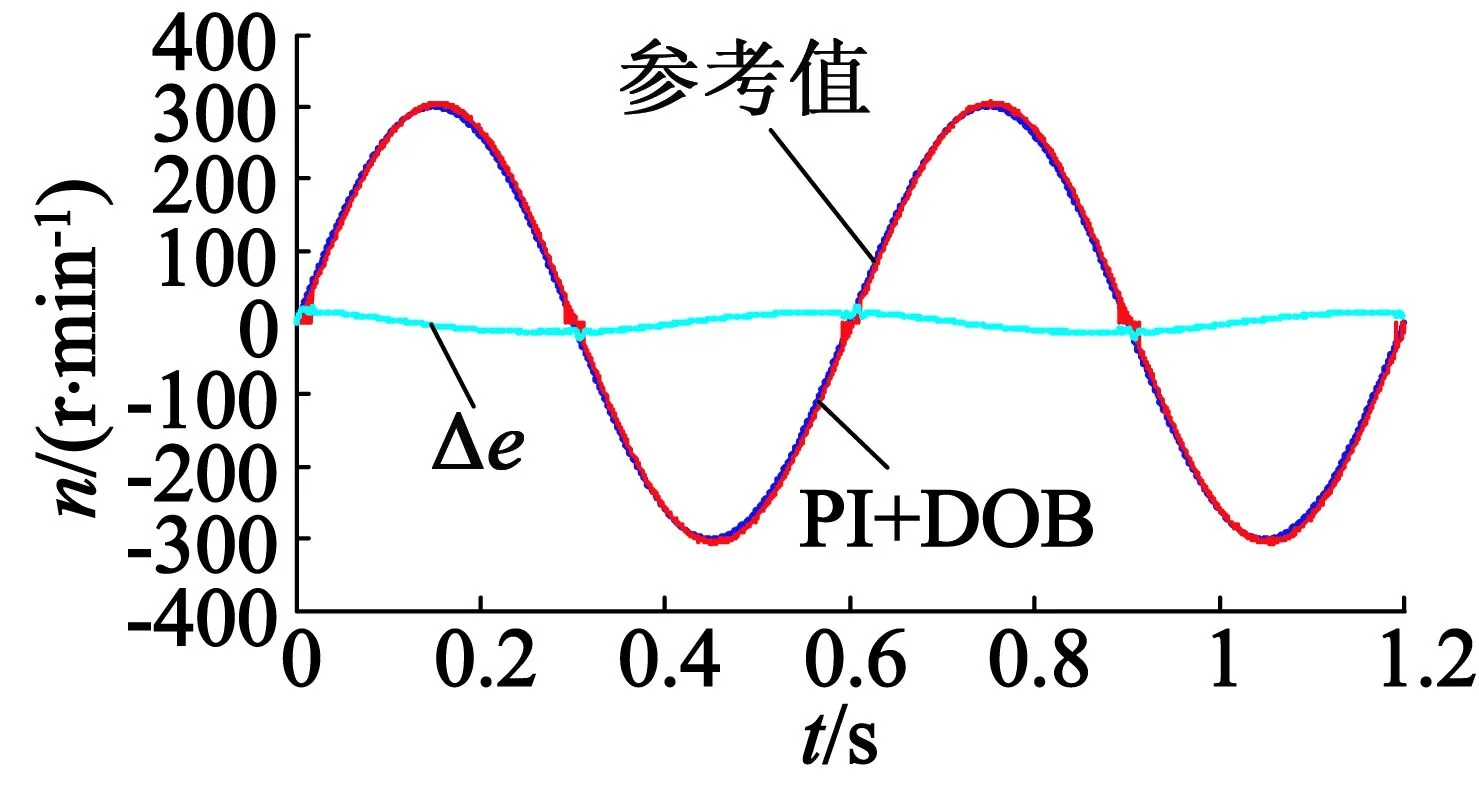
(b) 使用经典DOB

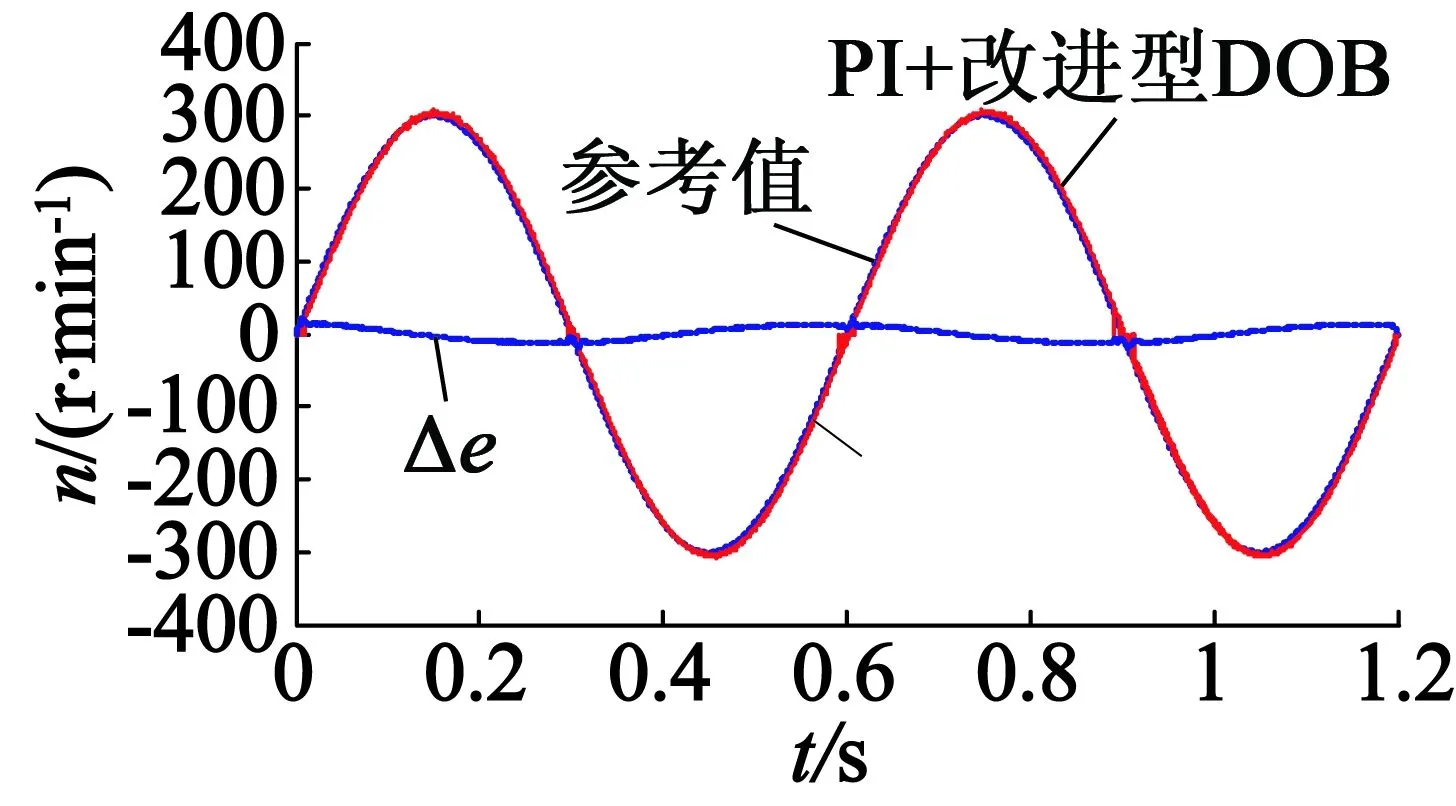
(c) 使用改进型DOB

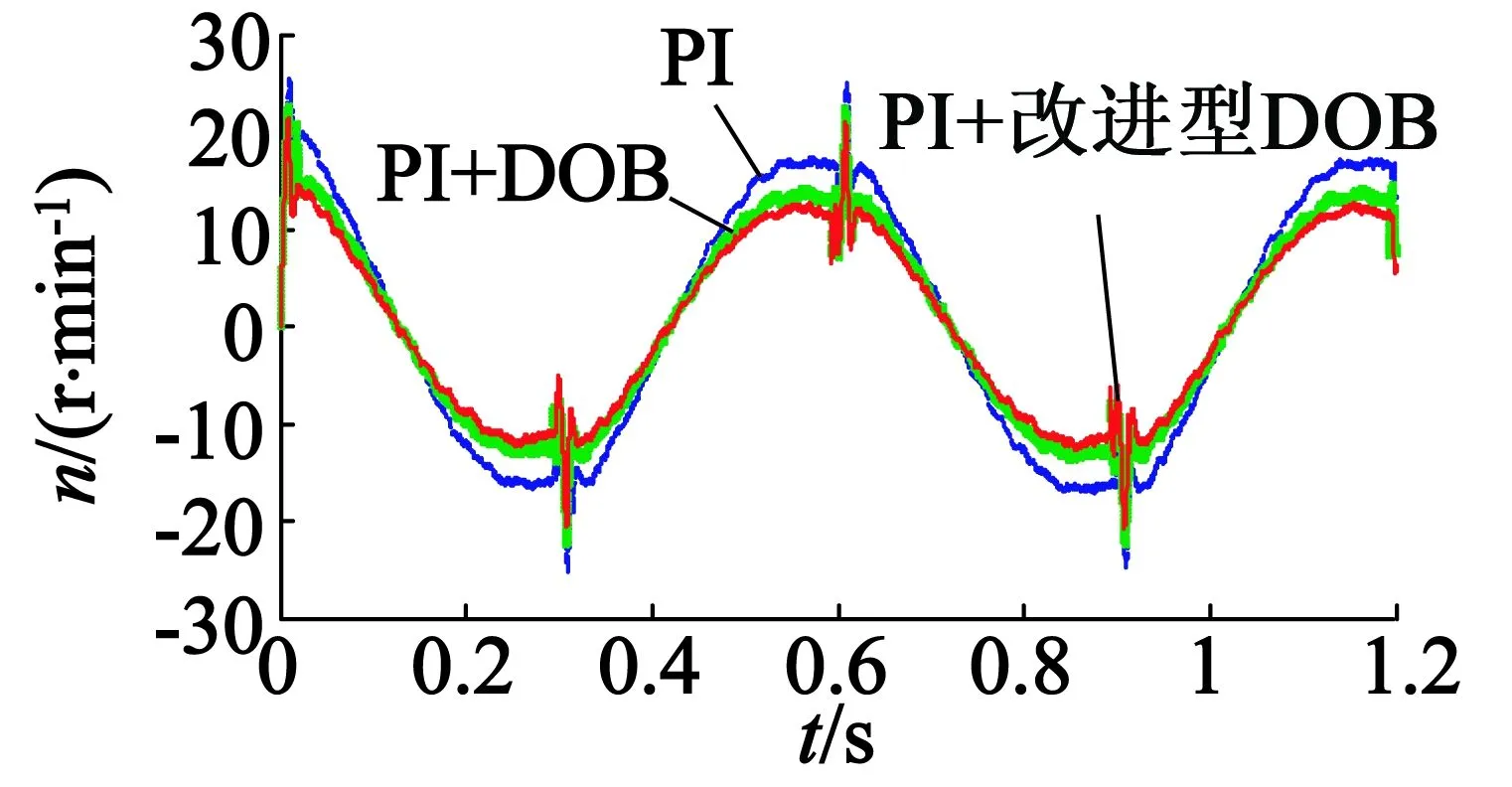
图15 速度偏差曲线

由速度偏差对比可知，分别使用单一PI控制、PI加经典DOB控制、PI加改进型DOB控制的速度跟随误差范围分别为-17～17 r/min，-14～14 r/min，-12～12 r/min。

3.3.2 加10%额定转矩

为模拟控制器对干扰力矩的抑制效果及突出实验现象，进行突加力矩干扰仿真实验，所加干扰力矩大小为10%的电机额定转矩。

速度为300 r/min时使用PI，PI加经典DOB和PI加改进型DOB、时的速度跟随效果如图16所示，速度跟踪偏差如图17所示。

(a) 使用PI

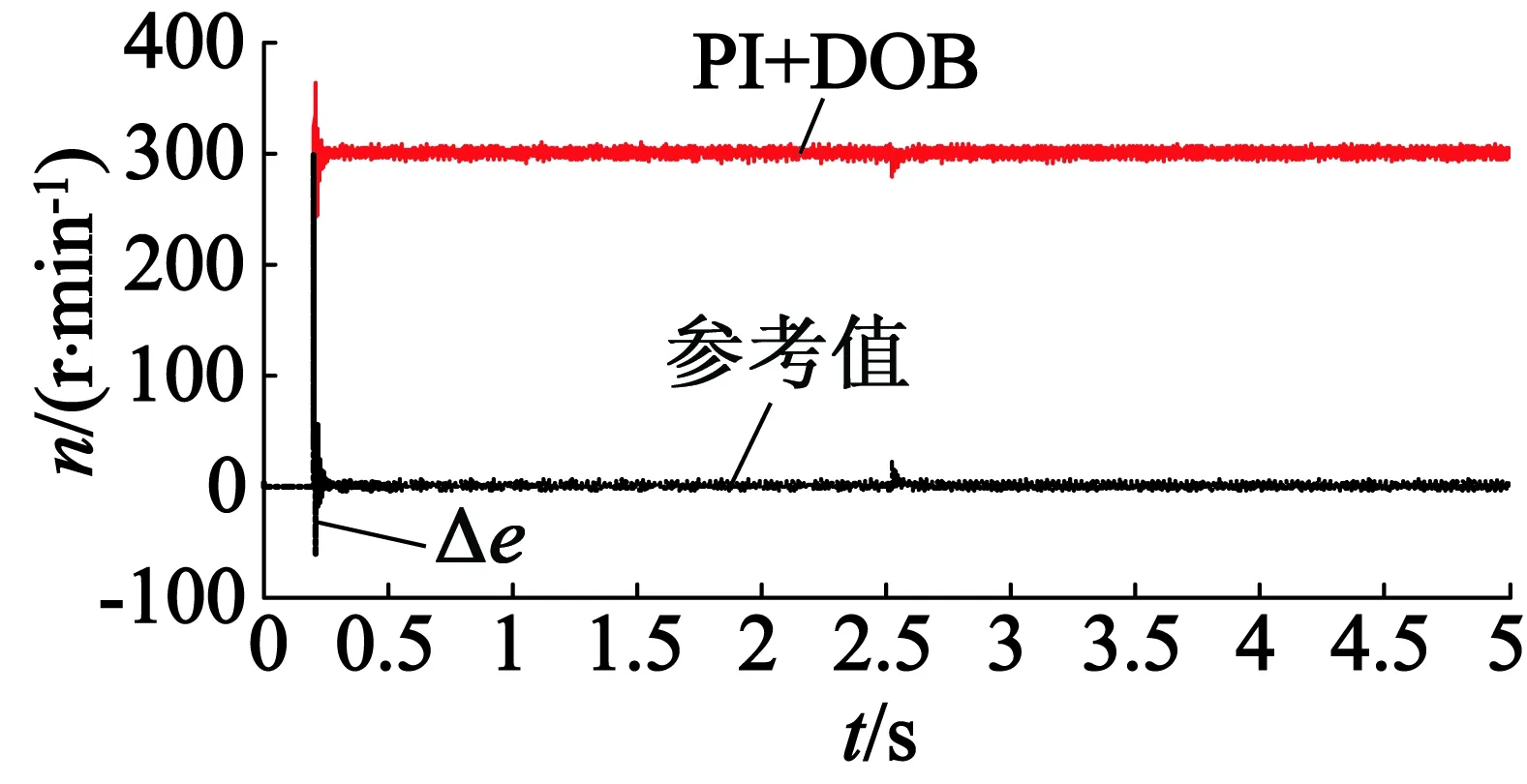
(b) 使用经典DOB

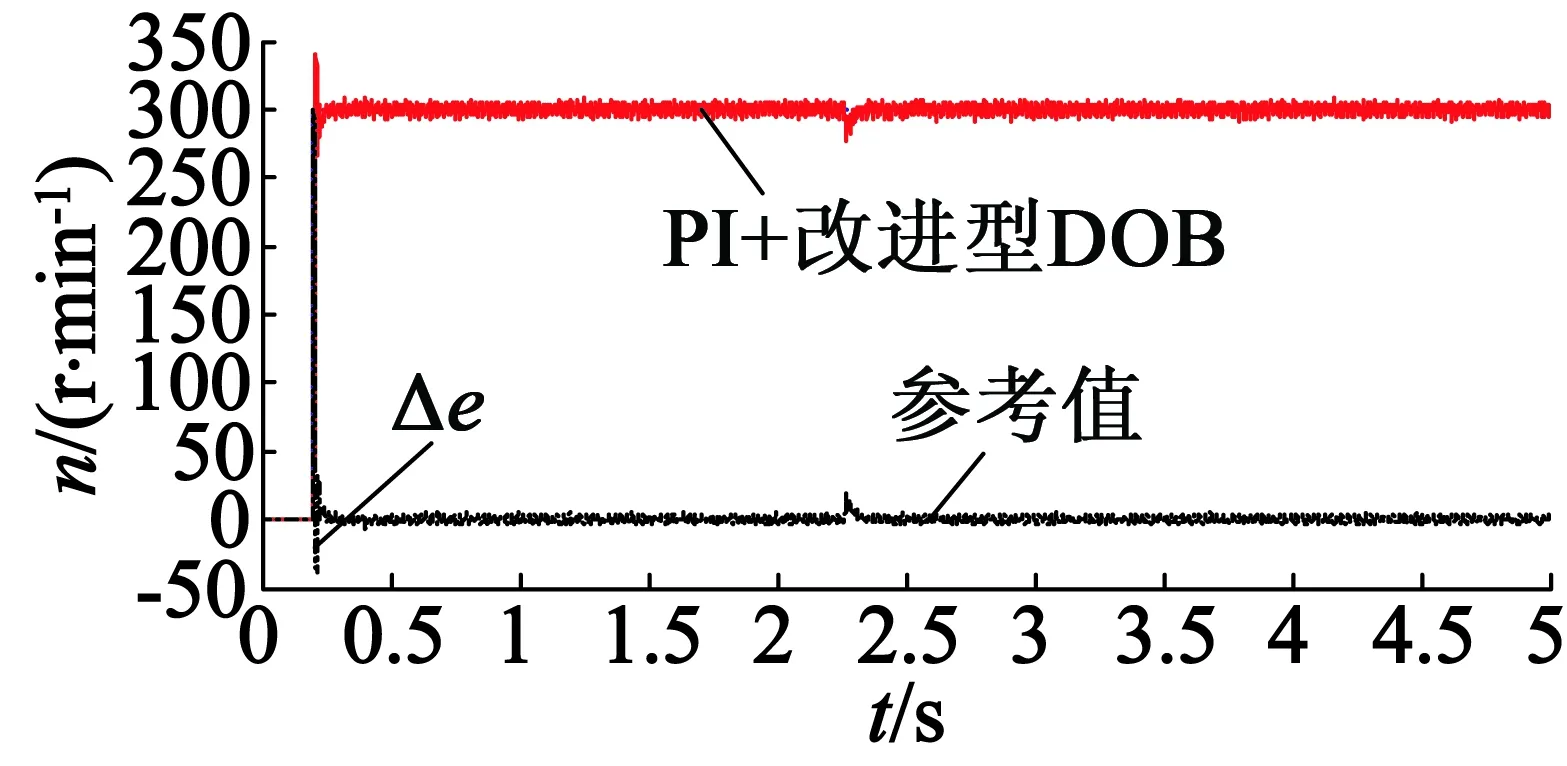
(c) 使用改进型DOB

图17 速度偏差曲线

由速度跟踪偏差曲线可知，在突加干扰力矩时刻，分别使用单一PI控制、PI加经典DOB控制、PI加改进型DOB控制的速度跟随误差最大分别为23.5 r/min，20 r/min，17 r/min。

4 系统验证

为验证加入改进型DOB后稳定平台对扰动的抑制能力，搭建稳定平台动态实验环境。控制系统使用以DSP作为主控芯片的控制器，实现相应的控制逻辑及控制算法。将稳定平台置于实验摇摆台上，人工以频率约为1 Hz，最大幅值约为16°摇摆摆台模拟载体姿态扰动。采集姿态测量传感器的实时动态数据，采用PI控制、PI加经典DOB控制和PI加改进型DOB控制时的俯仰方向姿态曲线如图18所示。

(a) 使用PI控制

(b) 使用经典DOB控制

(c) 使用改进型DOB控制

由以上俯仰方向姿态曲线可知，人工施加上述载体姿态干扰信号，使用单一PI控制时稳定平台俯仰角控制误差范围在-2.8°～3.1°之内；使用PI加经典DOB补偿时稳定平台控制角度误差范围约-1.3°～1.1°之内；使用PI加改进型DOB补偿时稳定平台控制角度误差范围约-0.6°～ 0.7°之内。

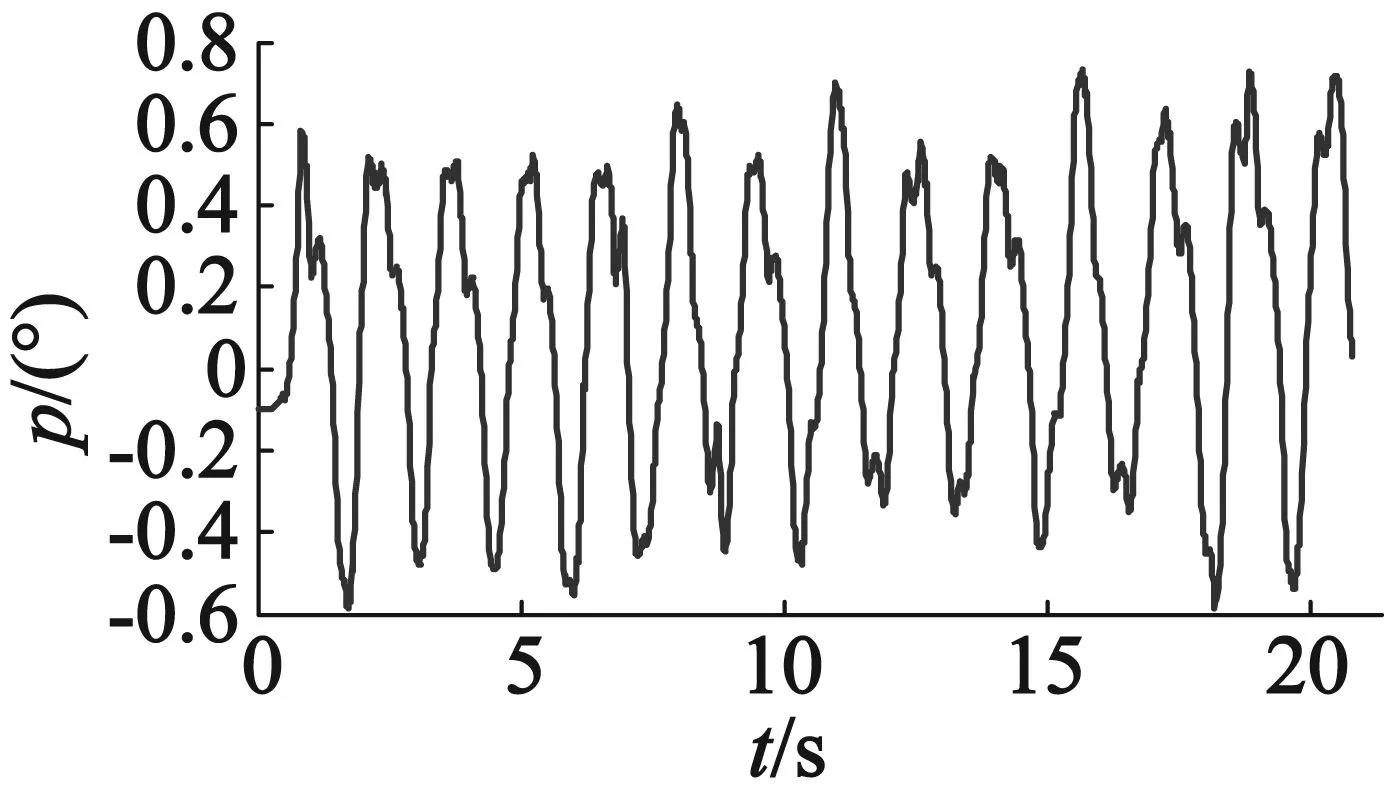
在稳定平台定位抖动实验中，设置K=10 000，使用S型加减速曲线，指令速度从0加速到800(脉冲频率)所用时间为30 ms。使用速度规划前稳定平台横滚方向与俯仰方向姿态如图19所示。使用速度规划后稳定平台横滚方向与俯仰方向姿态如图20所示。

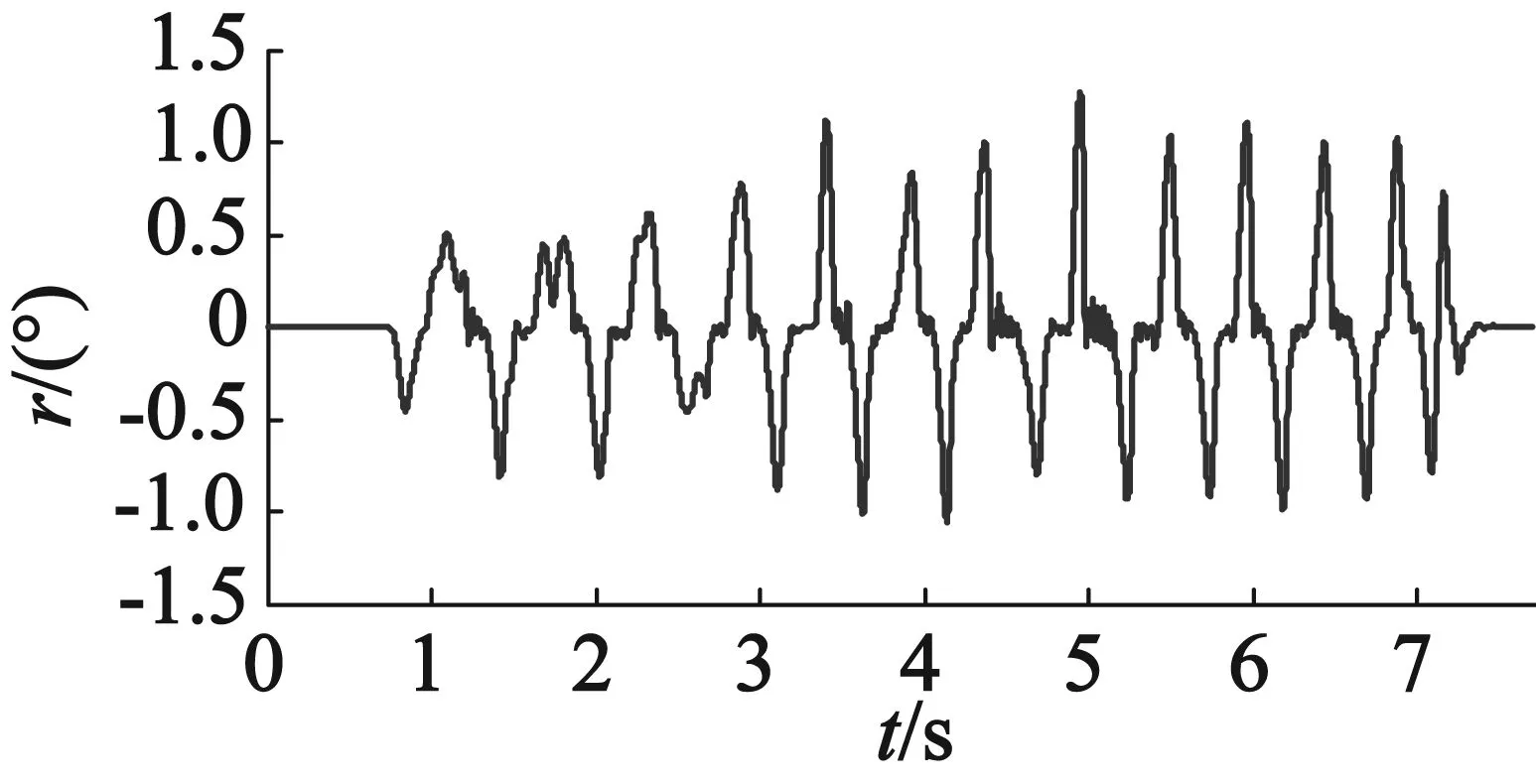
(a) 横滚角

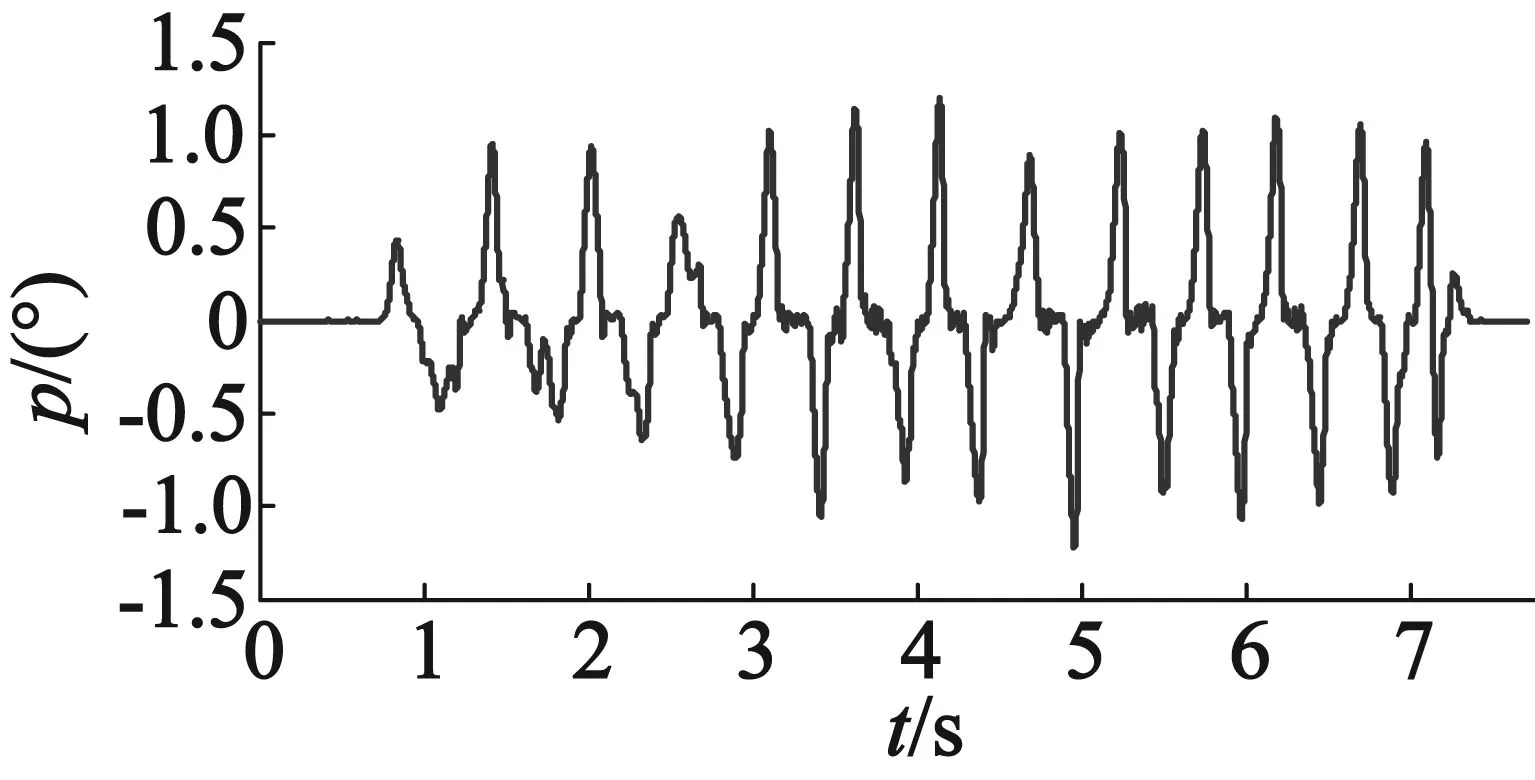
(b) 俯仰角

通过对比稳定平台使用速度规划算法前后姿态曲线可知，使用速度规划算法前稳定平台在定位过程中存在位置抖动，特别是在水平位置左右；使用速度规划算法后稳定平台在姿态调整过程运动更加平滑，并且明显提高了控制精度和稳定性，将稳定平台横滚角控制精度从-1.1°～1.3°以内提高到了-0.6°～0.7°以内，俯仰角控制精度从-1.3°～1.2°以内提高到了-0.6°～0.5°以内。

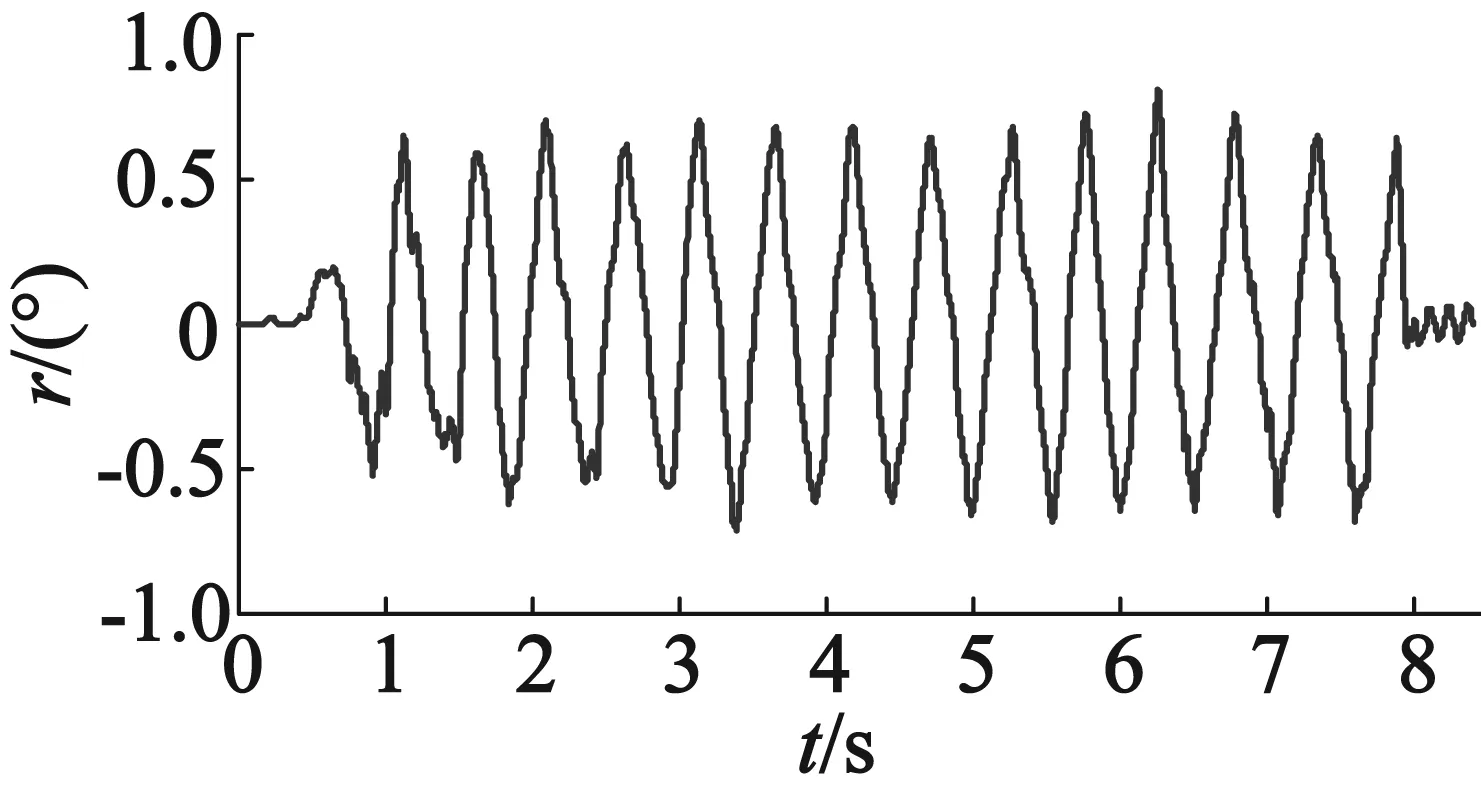
(a) 横滚角

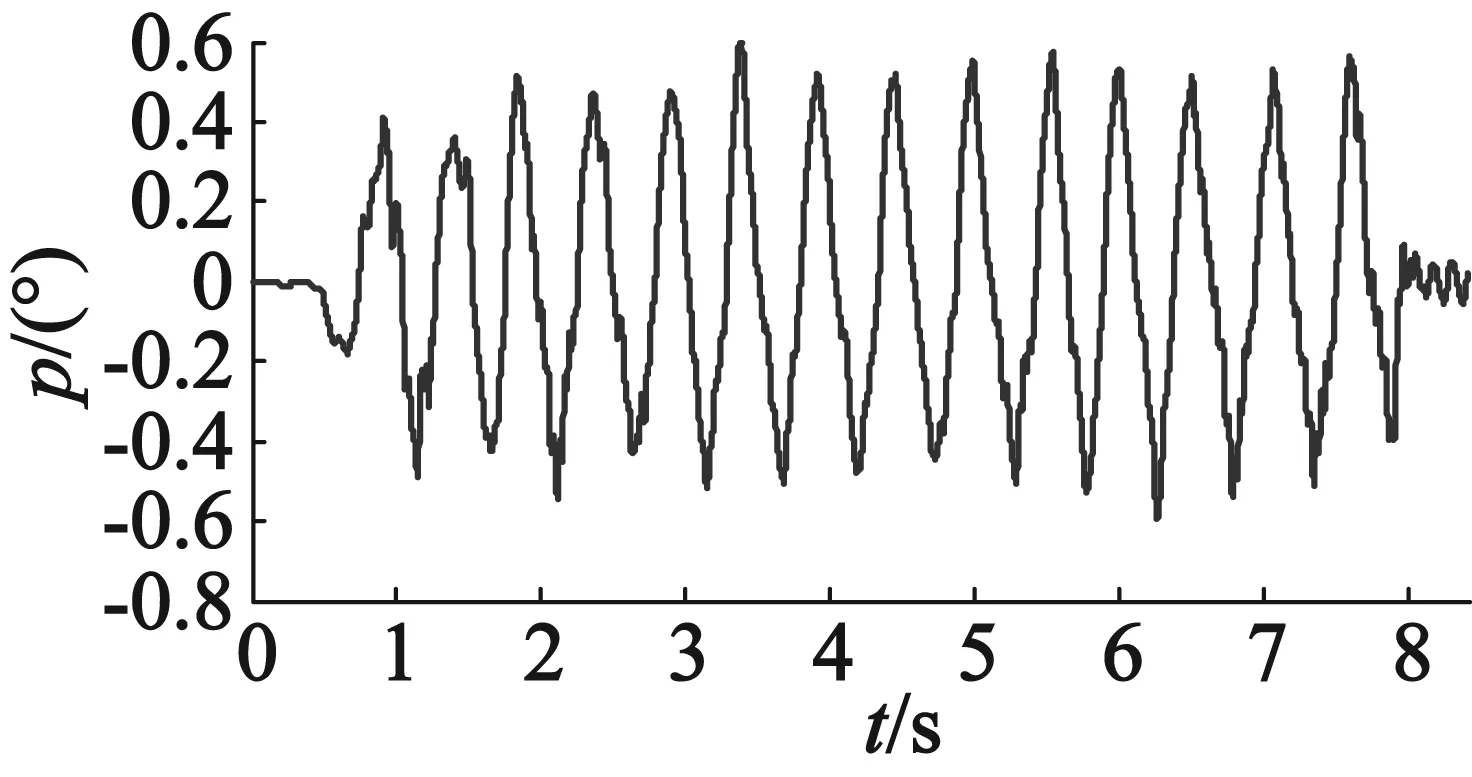
(b) 俯仰角

5 结 语

通过理论分析、数值分析、半实物仿真及系统实验，验证改进型DOB和速度规划算法在稳定平台干扰补偿中的应用，得出如下结论：

1) 相比于传统的PI控制方式，使用DOB及改进型DOB能够较好地估计出摩擦干扰力矩大小。

2) 将摩擦模型引入到系统中，仿真验证了DOB及改进型DOB算法的有效性。

3) 通过搭建半实物仿真实验平台，进行惯量盘作为负载、突加力矩模拟干扰实验，结果表明，使用改进型DOB相较于单一PI控制及加入经典DOB的控制系统，能够更好地跟踪速度指令。以惯量盘作为负载，跟随速度为300 r/min时速度跟踪波动降到12 r/min；跟随速度为500 r/min时速度跟踪波动降到20 r/min；在电机加载实验中，跟随速度为300r/min时速度跟踪波动降到17 r/min；跟随速度为500 r/min时速度跟踪波动降到11 r/min。

4) 经过稳定平台系统实物实验验证，使用改进型DOB后的平台控制姿态角度误差降0.7°之内，比使用经典DOB时的1.3°及单一PI控制时的3°的控制精度有显著提高；加入速度规划算法，明显抑制了平台定位抖动干扰，提高了稳定平台的控制精度及稳定性。