直线发电机在简谐振动下的感应电动势研究

伍 帆，吉 方，刘广民，吴祉群

(中国工程物理研究院机械制造工艺研究所，绵阳 621900)

0 引 言

在众多热电转换装置中，斯特林直线发电机具有适用热源广泛，可靠性高，工作寿命长的优点,已经在航天深空探索、军事便携供电、光热发电和微型热电联供等方面得到应用。如美国宇航局与能源部合作的Kilopower项目就是由核燃料裂变产生热量，再通过斯特林直线发电机完成热电转换[1]。在斯特林直线发电机方面，国外具有代表性的公司有美国Sunpower公司和以色列Qnergy公司，它们已进入商业化生产阶段[2]。而在国内，中国电子科技集团公司第十六研究所、中国科学院理化研究所、东南大学、沈阳工业大学等单位也展开了研究试验[3]。

与旋转发电机有所不同，直线发电机的应用场合是海浪发电[4]、对接各类活塞发动机发电[5]以及一般振动发电[6]，其动子通常并非做匀速直线运动，而是更接近简谐振动。此时会出现输出电压波形不规则的问题，为后处理带来困难。文献[5,7]主要从阻抗匹配的角度对直线发电机进行分析，重点在于功率和效率的均衡。文献[8]描述了简谐运动时的不规则电动势波形，但没有给出解决方案。文献[9-10]主要通过后处理电路对电输出进行改善。文献[11]使用异形永磁体组成Halbach阵列，在小振幅下产生较理想的感应电动势，但没有分析波形与振幅的关系。文献[12]针对简谐运动的条件，分析了海浪发电中直线发电机的幅频特性，说明了调节振幅的方法。本文通过分析和仿真发现，在简谐振动条件下，运动规律与磁场分布存在匹配较优的区间，通过选择合适的振动区间，可以有效改善电动势波形，提升输出性能。

1 简谐振动下感应电动势仿真分析

为说明简谐振动下感应电动势不规则的现象，以一台8极9槽三相直线发电机为例，使用ANSYS Maxwell软件建模并进行瞬态分析。直线发电机的动子由轴向充磁的N35永磁体与起导磁作用的10号钢交替排布。定子铁心为10号钢，永磁体轴向充磁。发电机的主要参数如表1所示，建立模型如图1所示。

表1 8极9槽圆筒型直线发电机结构参数

图1 8极9槽三相直线发电机结构

与旋转发电机的电角度相对应，直线发电机的位移以极距τp来衡量。令行程等于1倍极距，即振幅A=τp/2，振动频率f=50Hz，图1的振动中心(简称为第一种振动中心)位置下的空载电动势波形与磁链-位移曲线如图2和图3所示。

图2 第一种振动中心，1个周期内的电动势波形

图3 第一种振动中心，行程等于1倍极距时的

Ψ(x)曲线 调整发电机结构，以定子中间齿正对两磁体间隙处为振动中心(简称为第二种振动中心)，即以原来的τp/2位移处为新的位移原点。建立模型如图4所示。对应的空载电动势波形与磁链-位移曲线如图5和图6所示。

图4 8极9槽三相直线发电机结构

图5 第二种振动中心，1个周期内的电动势波形

图6 第二种振动中心，行程等于1倍极距时的Ψ(x)曲线

由图2和图5可知，当动子做小幅简谐振动时，不同振动中心位置对应的空载电动势波形不同。对空载电动势进行谐波分析如表2所示。在简谐振动条件下，三相直线发电机空载电动势存在较大的谐波分量，波形不规则，且电动势有效值不同，不利于负载平衡。

表2 振动行程等于1倍极距时三相直线发电机的空载电动势

2 简谐振动下感应电动势理论分析

根据法拉第电磁感应定律，即：

(1)

式中：e为感应电动势；Ψ为某相绕组的总磁链，t为时间。

针对直线运动进一步得：

(2)

而对旋转发电机有：

(3)

x(t)=Asin(2πft)

(4)

v(t)=2πfAcos(2πft)

(5)

设A，B，C三相的磁链-位移曲线符合正弦规律，且三者仅有120°的相位差别。对于第一种振动中心，设A，B，C三相磁链：

(6)

(7)

(8)

由式(7)和式(4)得：

(9)

将式(5)、式(9)代入式(2)可得B相的感应电动势：

(10)

同理可得A，C相的感应电动势：

(11)

(12)

对于第二种振动中心，设A，B，C三相磁链：

(13)

(14)

(15)

同理可得A，B，C三相的感应电动势：

(16)

(17)

(18)

由式(10)～式(12)以及式(16)～式(18)可知，在简谐振动下，感应电动势不是标准的正弦函数，而是复合函数。电动势波形的不规则是由磁场分布与运动规律匹配不佳造成的。

3 简谐振动下电动势波形的改善方法

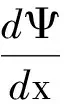
采用第一种振动中心位置，振动频率50Hz。初次设置振动行程为1倍极距，即A= τp/2，以确定Ψ(x)曲线零点的位置。有限元仿真得到的磁链-位移曲线如图8所示，Ψ(x)曲线在从-4.5～4.5mm(长度为1/3极距)的位移区间线性程度较好。将此作为新的振动范围，得到的感应电动势如图9所示。对其进行谐波分析，主要谐波分量为3次谐波，总谐波畸变率THD为3.08%。电动势波形接近正弦波，验证了优选振动区间对于波形改善的有效性。

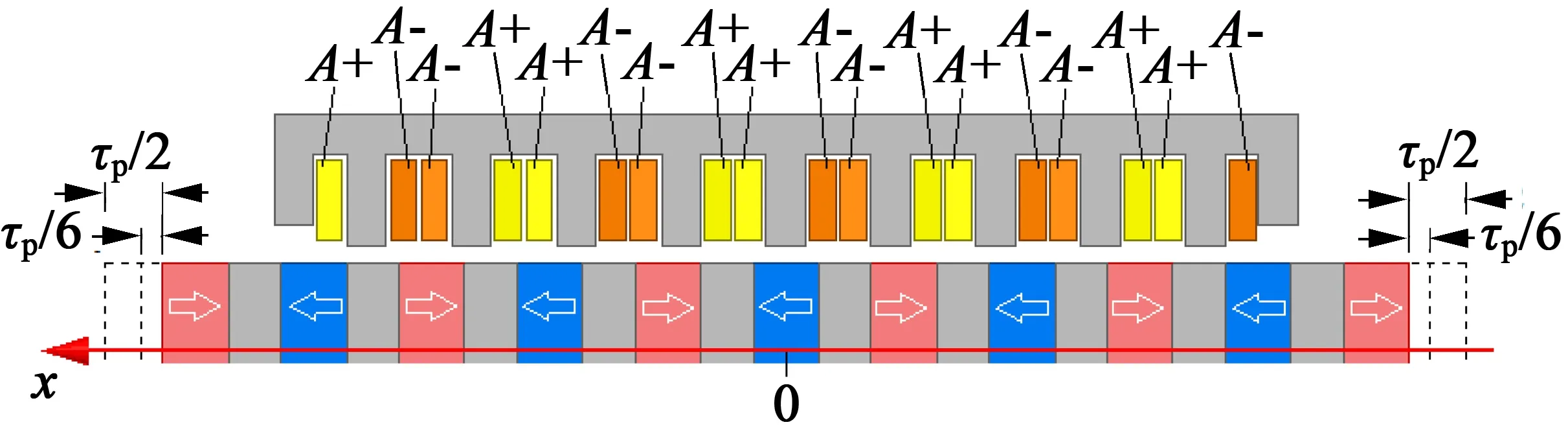
图7 8极9槽单相直线发电机，寻找适配的振动区间

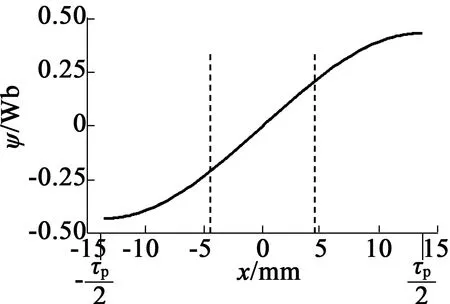
图8 单相直线发电机，行程为1倍极距时的Ψ(x)曲线

图9 优选振动区间(长度为1/3极距)后的感应电动势波形

4 简谐振动下三相与单相发电机的感应电动势比较

采用电动势矢量图法计算得：三相8极9槽(图1和图4)的绕组系数为0.945 2，单相8极9槽(图7)的绕组系数为0.630 1(图7)，说明在能充分发挥绕组优势的情况下，如匀速转动或长行程直线运动时，三相比单相更有功率优势。但针对行程较短(小于1倍极距)的简谐振动条件，须另作比较。按照表1参数，采用第一种振动中心位置，振动频率50Hz，对直线发电机在三相与单相、行程等于1倍极距(A=13.5mm)与1/3极距(A=4.5mm)下的空载电动势进行比较，如表3所示。

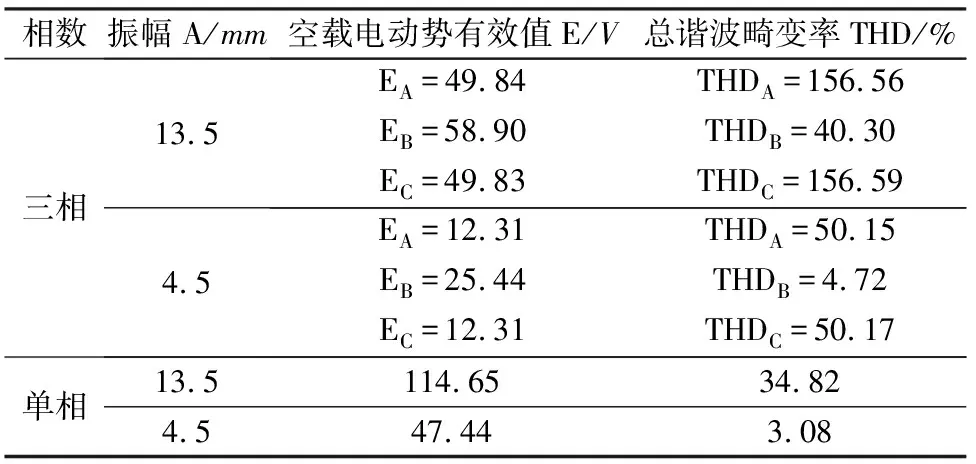
表3 简谐振动下，相同结构尺寸发电机，不同相数、不同振幅下的空载电动势比较

5 振动中心位置的稳定性

振动中心位置是否自然稳定，与振动中心附近定位力的方向有关。定位力由铁心与永磁体的结构和位置决定。本文对所述2种振动中心处的定位力进行分析，如图10和图11所示。由图1和图7所示，即第一种振动中心，此时在振动中心附近，当位移为正值时定位力同为正值；当位移为负值时定位力同为负值，即定位力与位移同向，定位力起到向外侧引出的作用，这表明振动中心处不是稳定位置。由图4所示，即第二种振动中心，此时在振动中心附近，当位移为正值时定位力为负值；当位移为负值时定位力为正值，即定位力与位移反向，定位力起到回复的作用，这表明振动中心处是稳定位置。对于振动中心不稳定的情况，可通过调整定子长度，改变定位力的相位，即对第一种振动中心，调整边端槽宽使定子总长由234 mm增至236 mm后，在振动中心附近定位力与位移反向，起回复作用，如图12所示，振动中心位置变为稳定。

图10 第一种振动中心，定位力与位移同向，振动中心位置不稳定

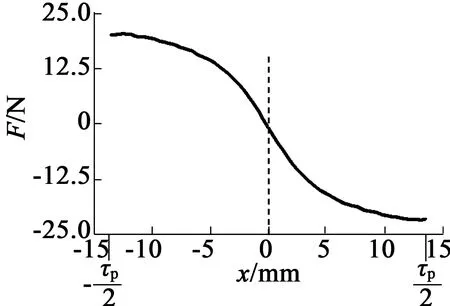
图11 第二种振动中心，定位力与位移反向，振动中心位置稳定

图12 调整定子长度后，定位力相位变化，在振动中心附近，定位力与位移反向，振动中心位置稳定

6 结 语

本文针对简谐振动条件下直线发电机的空载电动势进行分析。主要研究结论如下：

1) 简谐振动下，直线发电机的感应电动势通常不规则。采用单相绕组，通过选取Ψ(x)曲线零点附近1/3极距区间作为振动范围，可有效改善电动势波形。

2) 在小振幅条件下，单相直线发电机能充分利用Ψ(x)曲线在零点附近变化率最大的特性，综合输出特性更好。

3) 通过调节定子长度，可改变定位力的相位，使其在振动中心附近与位移反向，实现振动中心位置的自然稳定。

通过合理匹配运动规律与磁场分布，单相直线发电机可以实现较理想的电输出，适用于小振幅、高振频的斯特林发电系统。