中空形行波超声波电动机的研究

郎梦梦,曾劲松,张西平

(郑州大学，郑州 450001)

0 引 言

超声波电动机是利用压电陶瓷片的逆压电效应和电机定子的超声振动，借助电机定、转子之间的摩擦耦合，从而使电机转子运动的一种新型驱动器。超声波电动机具有无线圈、结构简单、设计灵活、动态响应快、质量力矩比大、高精度定位等优点[1-3]。随着科学技术的进步，特别在空间探测、光学工程、精密仪器、汽车产业等方面，超声波电动机的优势逐渐凸显[4-5]。

中空形行波超声波电动机因中空结构的特殊性，可应用于需要中空结构的驱动平台中，拓宽了其使用范畴[6]。中空形行波电动机可以被广泛应用于快速执行机构、电磁兼容要求高的机构、光学和医疗器械相关的机构。现有的超声波电动机以实心输出轴为主，因此中空形超声波电动机的设计极为迫切。

1 中空形电机运行机理

本文设计的超声波电动机定子呈中空的圆环形，压电陶瓷粘接在定子内表面，在压电陶瓷片上施加交流电压，通过压电陶瓷的逆压电效应在中空圆环上形成一个沿周向行进的面内弯曲行波。当行波在圆环上行进时，圆环外壁的质点会产生椭圆运动，从而在摩擦力的作用下推动转子旋转。

圆环的面内行波一般是由两相面内弯曲振动叠加而成。要在圆环上激励出理想的行波，必须先设法激发出圆环的2个同形、同频、正交的面内弯振模态。

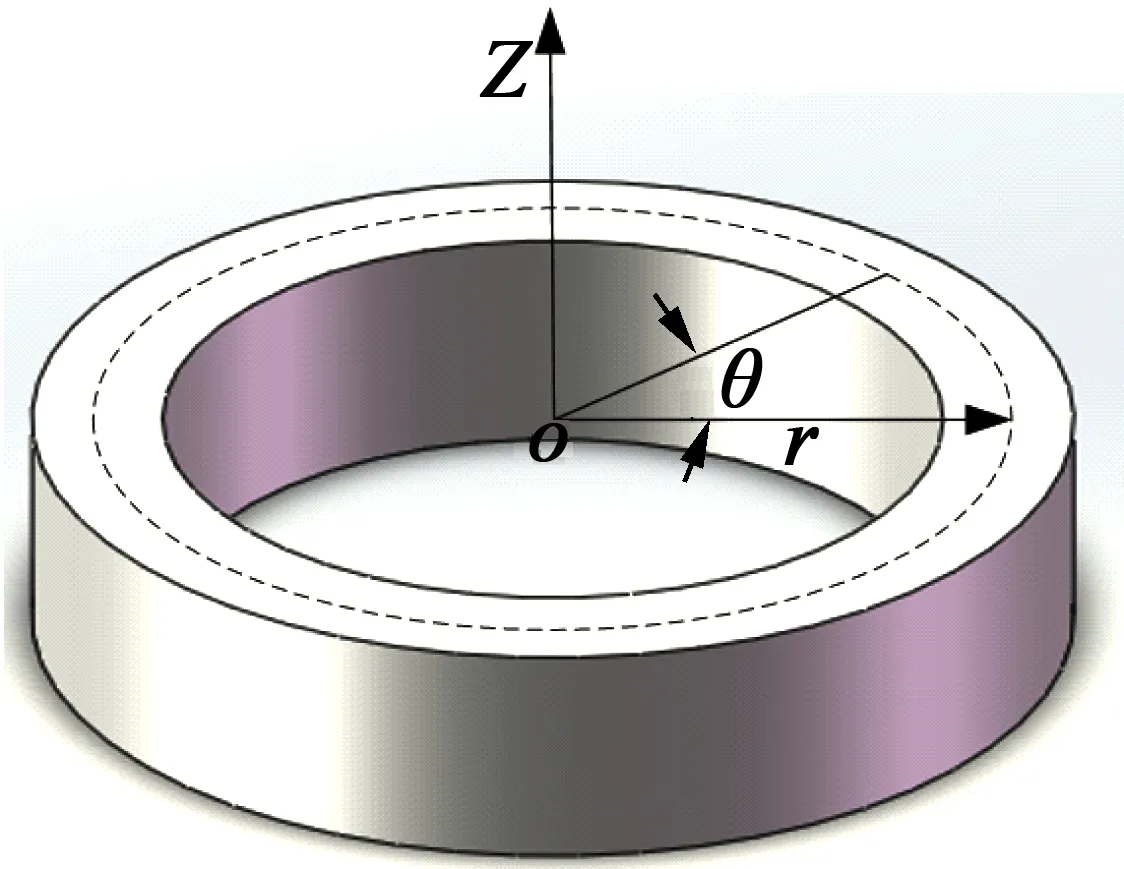
图1 定子环模型的极坐标

圆环的2个面内弯振模态在空间上需满足正交关系。图1为了中空定子的极坐标简图。在极坐标中，定子圆环中性层的2个径向振型函数可表示：

φ1(θ)=sin(nθ)

(1)

(2)

忽略干扰模态及结构阻尼的影响，当外界的2个振动激励作用在圆环上时，将激发圆环产生同频的n阶面内弯振模态响应[7]：

U1(θ,t)=φ1(θ)q1(t)=K1sin(nθ)cos(αnt)

(3)

U2(θ,t)=φ2(θ)q2(t)=K2cos(nθ)cos(αnt+δ)

(4)

式中:K1,K2分别代表圆环的2个面内弯振模态的响应幅值；αn代表振动激励的角速度，δ代表2个外界振动激励之间的相位差。

根据线性叠加原理，定子的位移响应：

U(θ,t)=U1(θ,t)+U2(θ,t)=

(K1+K2sinδ)sin(nθ-αnt)+

2K2cos(nθ)cos(αnt)cosδ}

(5)

U(θ,t)=K0sin(nθ-αnt)

(6)

由振动理论可知,在定子自由状态下,定子圆环沿圆周方向产生2阶、3阶以及高阶振动模态。实际上由于共振频率越高, 定子振动时内部发热越多，所以一般优先选择低阶模态作为工作模态。振动模态示意图如图2所示，虚线表示变形前定子形状，实线表示变形后的形状。

图2 振动模态示意图

2 中空形电机结构设计

中空形超声波电动机定子结构如图3所示。根据图3可知,此定子为中空的环形，为尽量有较大的中空空间,以及便于压电陶瓷片的粘贴，设定定子内圈为正十六边形。定子齿呈锥形，并呈周向分布在定子圆环上。齿与齿之间进行开槽设计，不仅可以放大周向位移，而且可以容纳磨损时的磨屑。

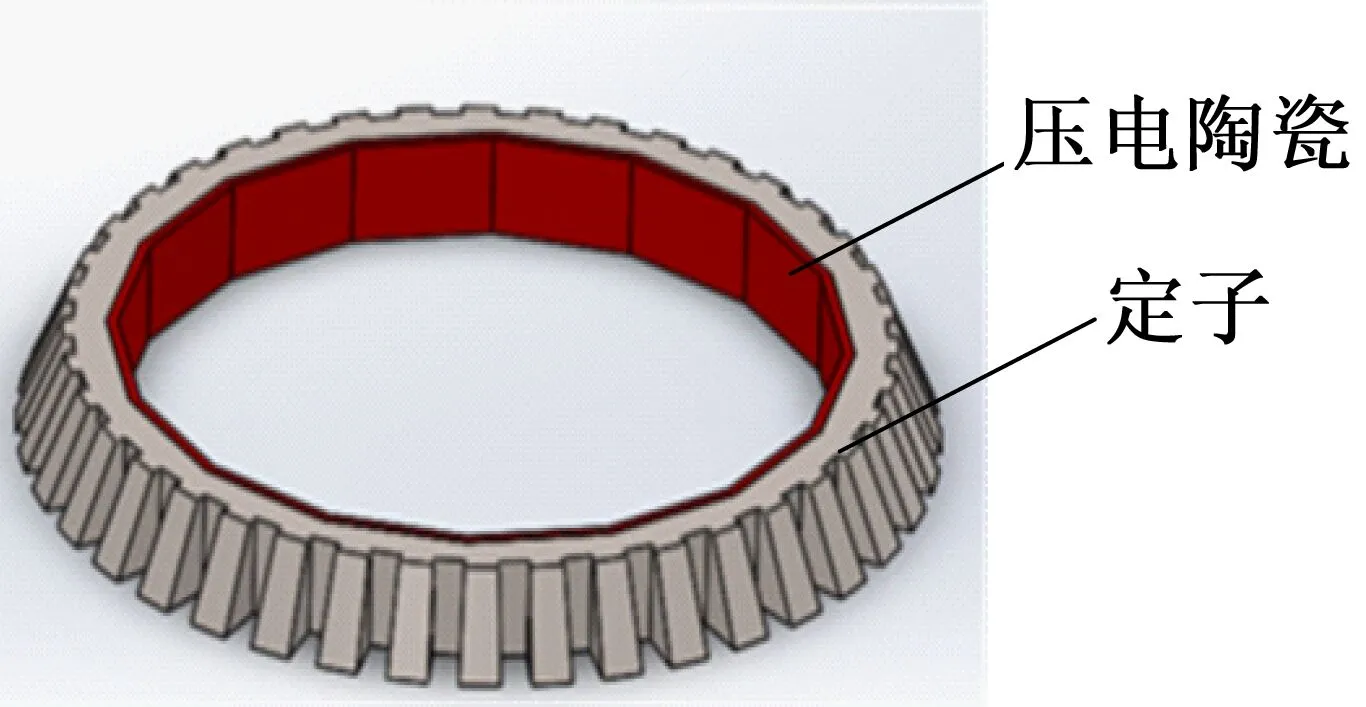
图3 定子结构图

中空形超声波电动机整体结构如图4所示，超声波电动机包括定子、转子、中空底座、薄壁轴承、摩擦材料以及预压力机构等主要构件。超声波电动机作为一种依靠摩擦力传递动力的驱动器，要求定、转子之间必须有预紧力作用，碟簧和卡簧的施加使得转子受到均匀的轴向预压力。定子外径较小的一端嵌套入转子的腔体中，环形的定子锥面与转子相嵌，锥形的接触界面使得转子具有良好的自动定心作用，且可将转子对定子的轴向预压力转化成周向预紧力，定子的圆周运动带动转子转动，可以得到较大的驱动力矩。为了确保将定子振动的能量尽可能完全传递给转子，提高能量利用率，转子的外径应与定子的外径相等，因为在相同条件下，定子外径质点的周向速度最大。支承的设计，应尽量减少对定子振动模态的影响，本文定子与中空底座通过螺纹连接，即在定子下底面的外圆周上开有细牙螺纹与底座连接，且定子与中空底座之间留出一定间隙。定子与转子的结构便于加工，实用性强。

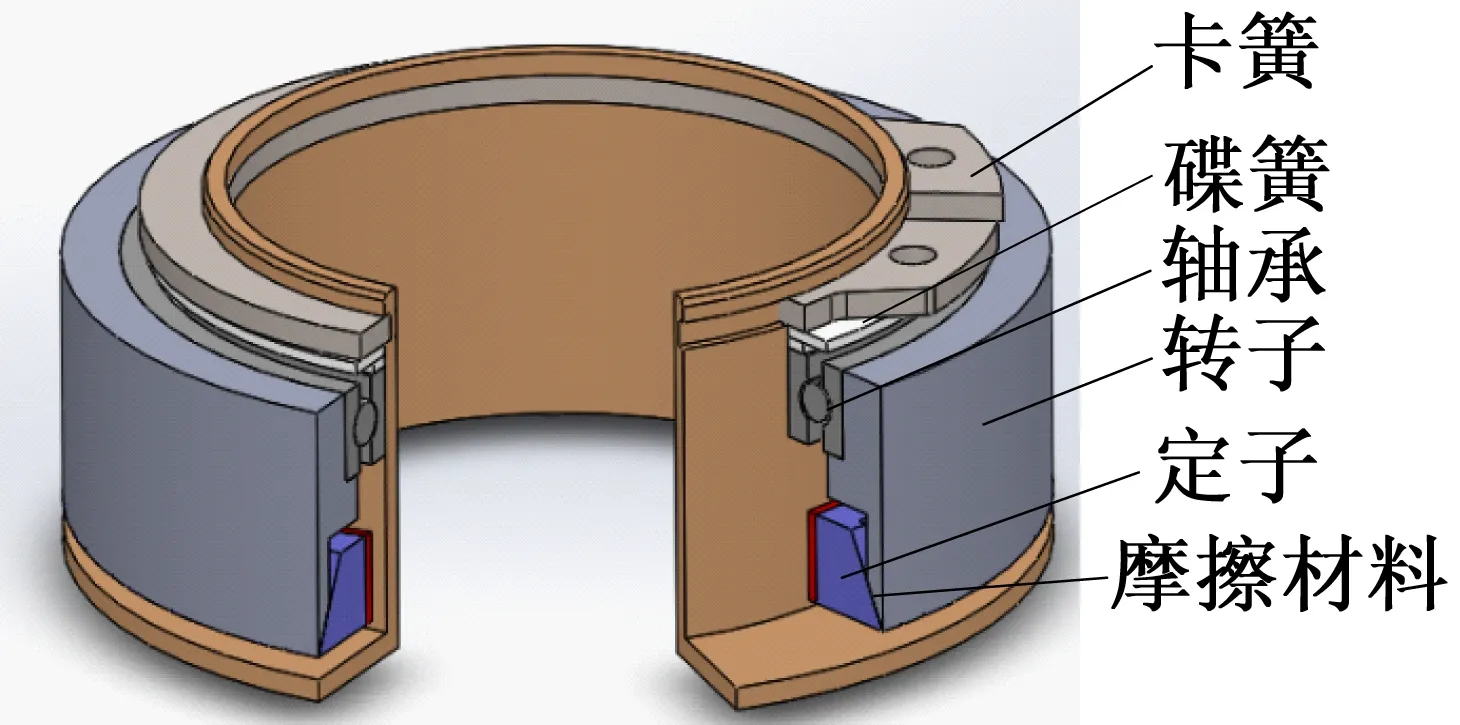
图4 整体结构图

3 定子模态分析

通过对中空形行波超声波电动机进行动力学分析,能够明确电机的机械特性[8]。模态分析可模拟超声波电动机定子的实际振动，从而确定定子的固有振动频率及振型。

运用ANSYS有限元分析软件对定子及压电陶瓷片组件进行实体建模，且定子和压电陶瓷片的接触采用粘接处理，并进行模态分析。本文定子的材料采用316L钢，压电陶瓷材料选用PZT-8。

为了满足实际应用需求，设定环形定子下底面直径为42 mm；为了便于转子与定子的相嵌，锥形定子齿的斜率不宜过高，设定环形定子上底面直径为38 mm，定子高度为4 mm。为使定子有较大的中心孔，即正十六边形内切圆的直径与定子下底圆的直径比尽量接近1，设定正十六边形的边长为6.5 mm。考虑到加工精度，齿与齿之间的间隔宽度为1.4 mm，且齿根圆的半径为18.5 mm,齿数为40。

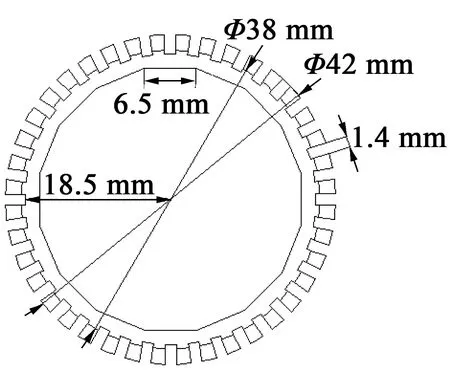
图5 定子尺寸图

对超声波电动机在19～40 kHz频率范围进行10阶模态分析，模态分析中，设置边界条件为自由振动，忽略阻尼。分析结果如表1所示。

因高阶面内振动的振动频率相对较高，相应造成较大的振动消耗，所以本研究选用面内四阶模态振型，即振动阶数为1阶与2阶。由表1可知，面内四阶振动模态频率为21.542 kHz，与其相邻的3阶振动频率相差5 126 Hz，相差较大，激励时不会造成模态混叠，可以证明电机在工作时是稳定的，同时也证明了本文设计的中空式结构的电机定子的合理性。面内四阶模态频率图如图6、图7所示。

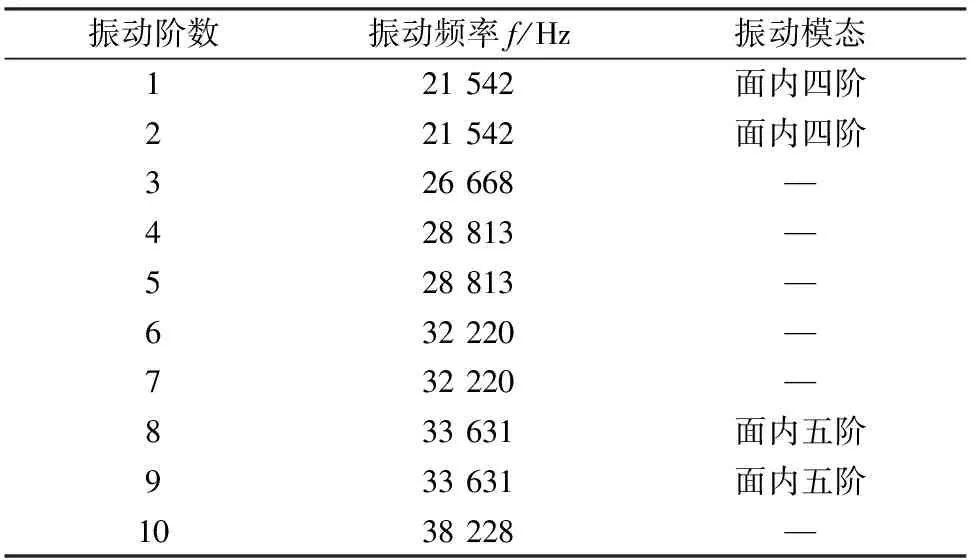
表1 定子模态频率

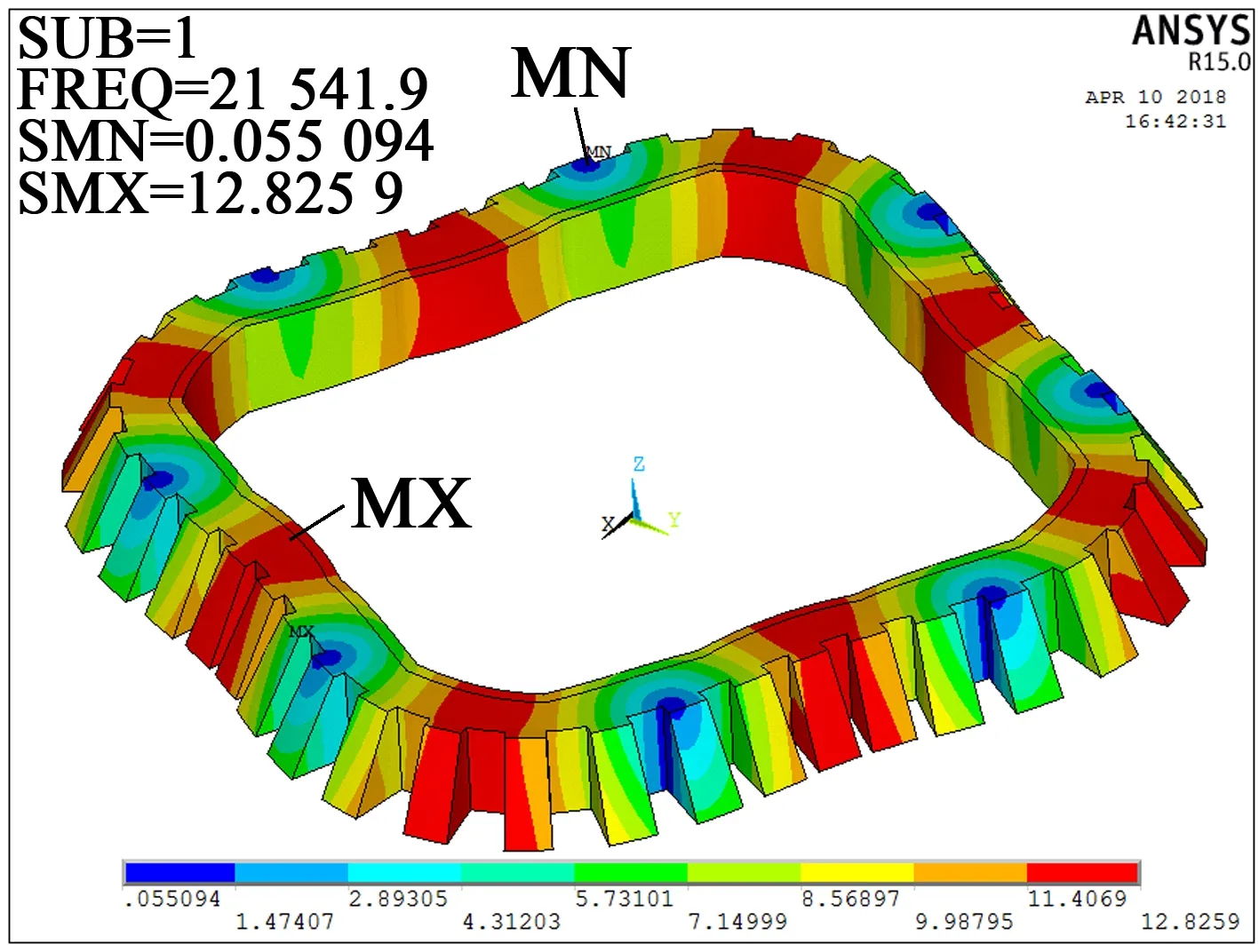
图6 面内四阶模态振型1

图7 面内四阶模态振型2

4 定子谐响应分析

中空形行波超声波电动机的运转性能与定子的振幅有很大关系，对定子进行谐响应分析，可模拟电机的实际工况，计算出定子在特定激励电压和频率下的振幅。且谐响应分析可验证模态分析所选择的振动频率是否为最佳工作频率。

根据面内行波运行机理并结合实际要求设计中空超声波电动机压电陶瓷的粘接方式，图8为定子施加电压的俯视图，16片压电陶瓷紧贴在定子内十六边形的孔内，压电陶瓷的极化方向为从正号到负号，即从压电陶瓷片的内侧向外侧极化。接触定子基体一侧的压电陶瓷片接地，另一侧的压电陶瓷片电压按照sin，cos，-sin，-cos的顺序激励出行波。

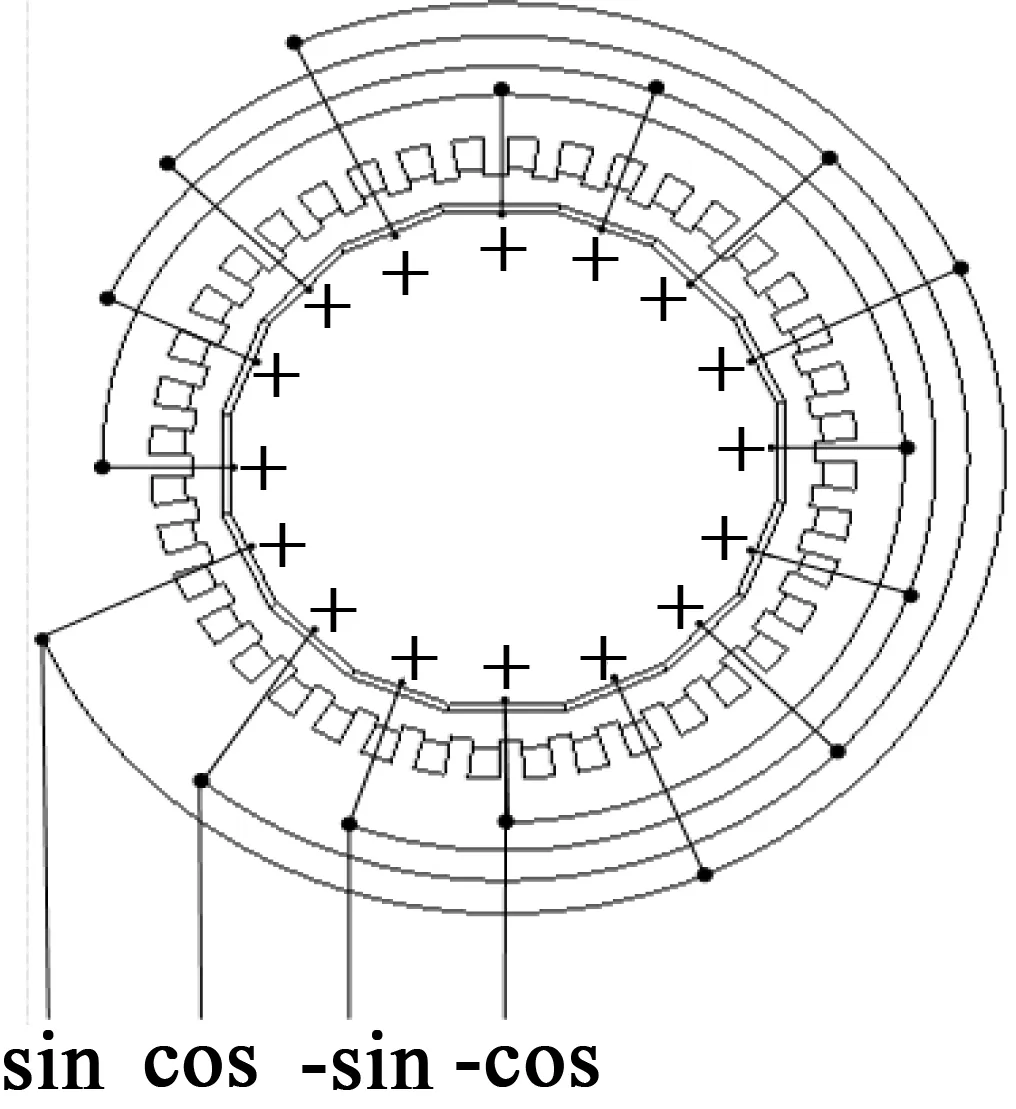
图8 四相接线示意图

依据工作模态频率附近的范围内进行谐响应分析，对此定子施加峰峰值为160V，频率范围为21.2～21.7 kHz的交变电压，设定40个子步，这样缩小了计算范围，大大缩短计算时间。在柱坐标系中提取定子上与转子相接触的某一质点的径向位移与周向位移，如图9所示。由图9可知，在所选频率范围内，质点在频率为21.375 kHz时达到峰值，接近模态分析频率。且径向位移Sr为3.3 μm,周向位移Sc为2.95 μm，周向位移与径向位移比为0.9，具有良好的输出状态，满足预设要求。

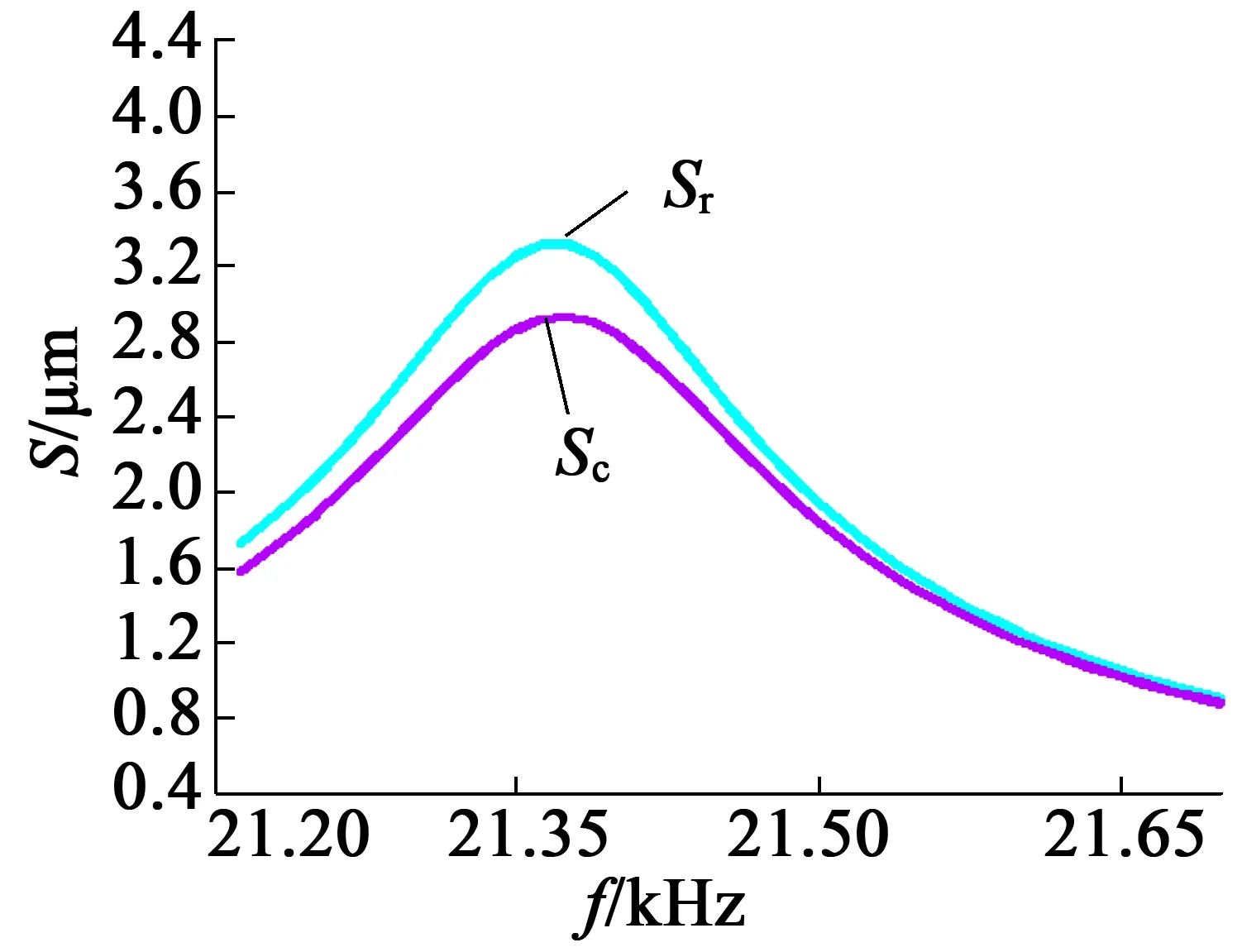
图9 质点位移图

为提升电机的运转性能，可通过提高电机定子表面质点周向位移和径向位移来实现，一种行之有效的方法是在合适的模态基础上增大激励电压。通过施加不同峰峰值的交变电压，频率为面内四阶振动的共振频率，研究质点位移随电压变化情况，如表2所示，定子质点的周向位移与径向位移随着电压的升高呈线性分布，且都具有较大的位移比。

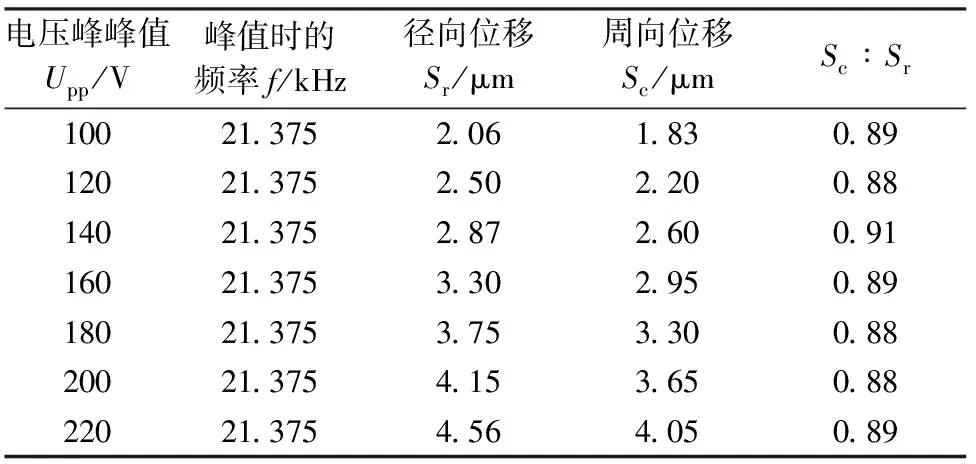
表2 质点位移变化

5 结 语

电机较为理想的工作状况是电机转子运转平稳且电机定子与转子无相对滑动。实现电机良好运转，要选择合适的振动模态，电机定子表面质点应有较大的周向位移和径向位移，且周向位移和径向位移之比尽量大。本文研究的是一种中空形行波超声波电动机，定子的设计一改传统的结构，定子齿呈锥形，设计新颖，内孔为正十六边形，不仅便于压电陶瓷片的粘贴，也有利于中心孔空间的较大利用。

依据实际的需求，并结合理论，进行合理的尺寸设计，选择模态振型，通过对定子施加不同电压值进行谐响应分析，证明电机输出性能较好、随时可调速度快，以此验证结构设计的合理性。