霍尔位置检测的电动汽车永磁电机矢量控制

易 磊，曲荣海，李新华，孔武斌

(1.湖北工业大学，武汉 430068；2.华中科技大学，武汉 430074)

0 引 言

内置式永磁同步电动机具有高效率、高功率密度和较低的转矩脉动等优点，被广泛用于电动汽车驱动领域。相对于无刷直流电动机的六步换相控制，永磁同步电动机磁场定向控制产生的转矩脉动和噪声较小，效率高，但磁场定向控制需要得到高精度的转子位置信息。传统的转子位置检测方法分为有位置传感器法和无位置传感器法，有位置传感器法是在永磁同步电动机转轴上安装旋变、编码器等，但位置传感器成本高且易受环境干扰[1]；无位置传感器法省去机械传感器，可降低系统成本，但算法实现复杂，并且转子初始位置检测和带载起动困难，不适用于电动汽车应用场合[2]。

霍尔位置传感器具有安装简单、体积小、成本低等特点，但是其输出位置信号分辨率低，每个电周期只有6个离散的转子位置信息，不能满足磁场定向控制的要求。因此通过对低分辨率转子位置信息进行位置估算算法的研究，得到与高精度位置传感器类似的转子位置和速度，已经成为低分辨率位置估算转子位置技术的关键[3-7]。

本文提出采用低分辨率霍尔位置传感器进行电动汽车用内置式永磁同步电动机磁场定向控制的方法。内置式永磁同步电动机转子结构为V形磁钢，利用与转子同轴连接的磁环和安装在端盖上的霍尔位置传感器检测转子离散位置。在6个离散转子角度基础上通过平均速度法获得连续转子位置，从而实现磁场定向控制，降低电机转矩脉动，提高系统舒适性。

电动汽车运行时需要满足低速大转矩和高速恒功率的要求，在电池容量和安装空间受限的前提下，为提高电机运行速度，需要采用弱磁控制。由于电动汽车运行工况复杂，并且存在交直轴电感和磁链等时变问题，通过采用基于电压外环的弱磁控制，实现电机弱磁升速，提高系统控制的鲁棒性。

1 永磁电机数学模型和矢量控制

内置式永磁同步电动机通过利用磁阻转矩可有效实现大扭矩和高转速要求，采用恒相幅值变换得到d,q旋转坐标系下永磁同步电动机的数学模型如下。

电压方程：

(1)

磁链方程：

(2)

电磁转矩方程:

(3)

式中：ud，uq分别为d，q轴电压；id，iq分别为d，q轴电流；Ld，Lq分别为d，q轴电感；Rs为定子电阻；ψf为永磁体磁链；ωe为转子电角速度。

电动汽车用内置式永磁同步电动机采用转矩控制方式，基于最大转矩电流比控制策略来实现d，q轴电流分配，通过霍尔位置传感器和估算算法得到转子位置，控制系统框图如图1所示。

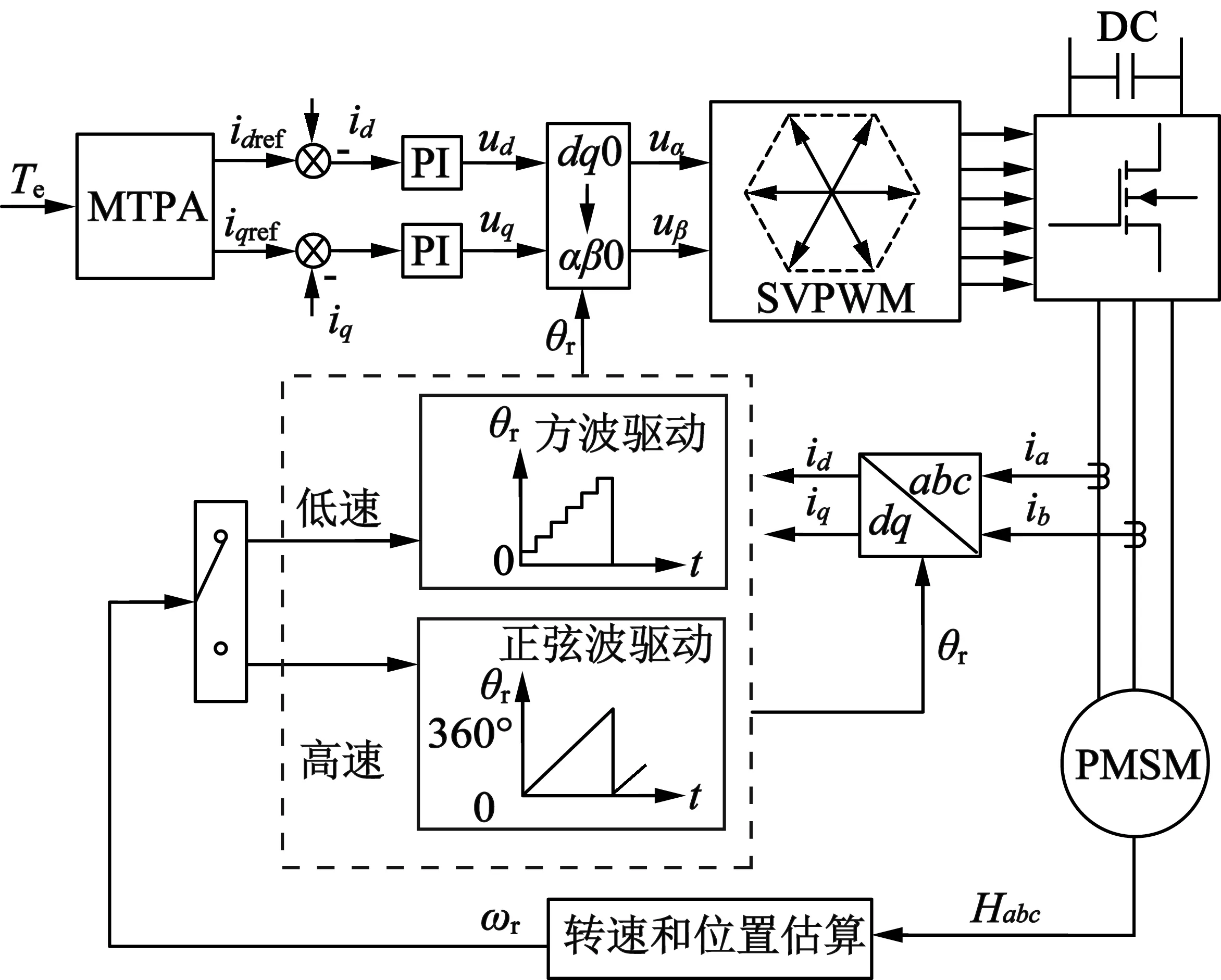
图1 基于霍尔位置传感器的永磁电机磁场定向控制

从图1可看出，采用霍尔位置传感器的永磁同步电动机，起动和低速阶段坐标变换采用离散转子位置，高速后采用位置估算算法得到连续的转子位置信号，从而实现起动过程中方波和正弦波电流切换。基于转子磁场定向的矢量控制需要合理分配定子的电流大小和相位，而定转子磁场相位关系主要通过位置估算算法得到，因此能否通过霍尔位置传感器得到精确的转子位置信号直接影响控制性能的好坏。

2 转子位置估算原理

2.1 霍尔位置传感器

永磁同步电动机转子位置通过3路互差120°的开关型霍尔位置传感器得到，考虑到电枢反应会造成气隙磁场畸变，因此实际应用中采用与转子磁钢同轴连接的磁环。当电机旋转时，3路霍尔传感器输出互差120°、脉宽180°电角度的方波信号，其中逆时针运行时霍尔位置信号如图2所示。

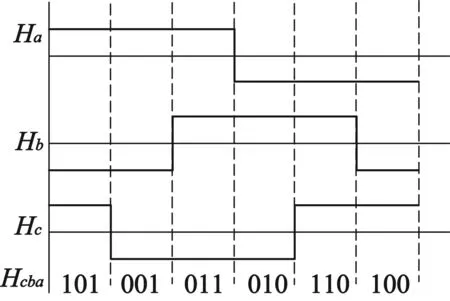
图2 逆时针霍尔位置信号

从图2可以看出，电机逆时针旋转时霍尔信号相序为a，b，c，对应霍尔状态Hcba为1-3-2-6-4-5。同理，可以根据旋转磁场关系得到，顺时针霍尔信号相序为a，c，b，对应霍尔状态Hcba为1-5-4-6-2-3。由此，可以根据霍尔状态变化序列，判断出电机的旋转方向，实现在霍尔边沿处由不同状态下转子离散位置校正。

根据霍尔传感器和定子三相绕组轴线相对位置，得到低分辨率转子位置和霍尔状态关系，如图3所示，其中转子位置定义为d轴与A轴夹角。

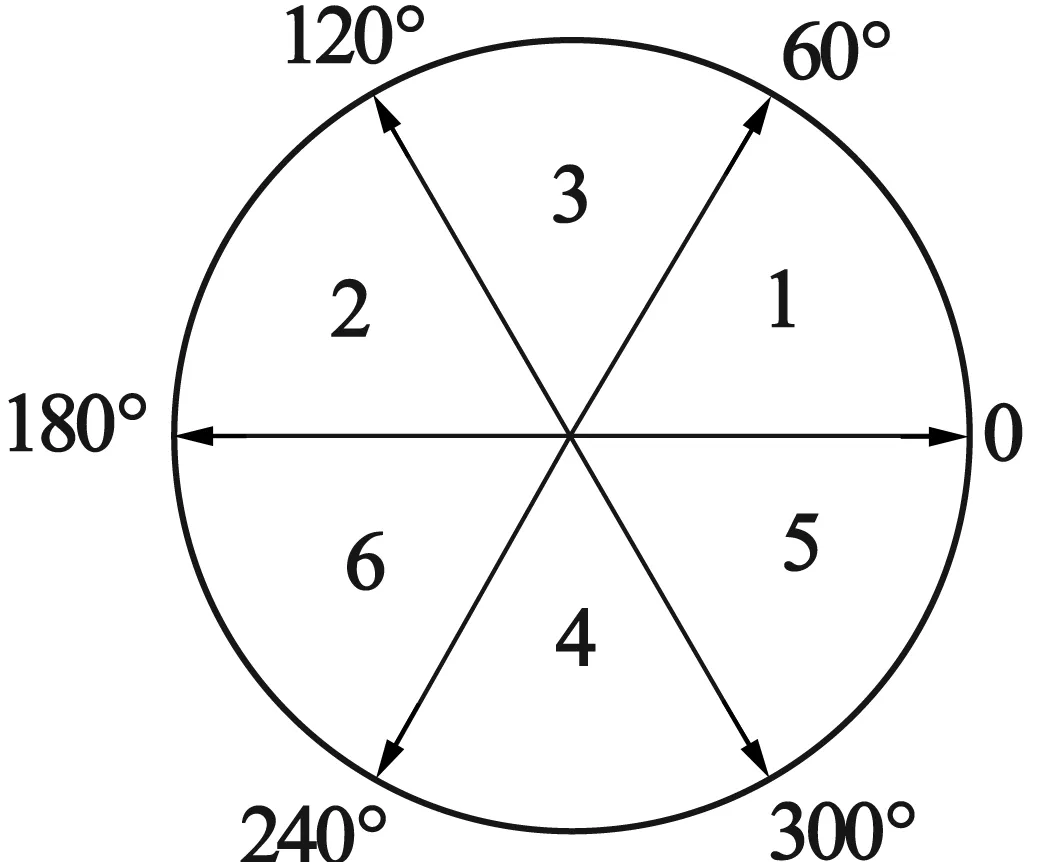
图3 霍尔状态与低分辨率转子位置

由图3可直观看到，当霍尔边沿发生时，根据不同霍尔状态，可得到对应的低分辨率转子位置。电机处于不同旋转方向下，对于同一霍尔状态而言，边沿处校正的转子位置有所不同，其中逆时针旋转对应的低分辨率转子位置比顺时针小60°。由于电机起动和低速阶段的位置估算算法误差较大，此时坐标变换采用扇区的中间角度，由图3可知，存在±30°角度误差，对应的电流驱动为方波电流，转矩脉动较大。在高速下，基于霍尔位置传感器信号，通过位置估算算法可得到电机连续转子位置，实现矢量控制。

2.2 转子位置估算方法

由于3路霍尔位置传感器每个电周期只提供6个离散的位置信号，无法满足永磁同步电动机矢量控制要求，因此需要利用位置估算方法得到连续的转子位置,常用的位置估算算法包括平均速度法和平均加速度法等。

其中，平均速度法适用于电机稳态运行，但是电机起动或者转速突变时，可能会存在估算误差。在一阶算法中引入平均加速度法能够解决转速突变情况下带来的误差，但是阶数的提高必然导致算法过于复杂化，实用性不足。同时，在上述2种方法中，存在一个最小转速使得算法不能成立，因此需要单独设计起动方法[8-10]。

采用平均速度法的位置估算算法，其基本原理：根据电机的机械时间常数远大于电气时间常数，假定每60°霍尔区间内转子速度是均匀的，因此可以利用上一个区间的平均速度作为下一个区间的初始速度，通过对速度的积分得到连续的转子位置信号，在霍尔边沿处对转子位置进行强制校正以消除估算误差，转子位置估算算法示意图如图4所示。

图4 转子位置估算算法示意图

对于图4中t时刻转子位置θest计算公式：

(4)

θest=θi+kωi-1Ts

(5)

θi≤θest≤θi+1

(6)

式中：ωi-1为扇区i-1内平均速度；Ti-1和Ti分别为扇区i-1，i所用时间；Ts为采样周期；k为采样次数；θi-1，θi，θi+1分别为低分辨率位置信号。当到达霍尔信号边沿处时即进行强制校正，如式(6)所示，经过位置校正后，消除估算累计误差。通过位置估算算法得到连续的转子位置信号，根据磁场定向控制的原理实现永磁同步电动机转矩控制[11]。

3 基于电压外环的弱磁控制

为解决永磁同步电动机因高速运行造成电压过高而导致电流调节器饱和的问题，提出弱磁控制策略以降低电机电压，常用的控制方法包括超前角弱磁调速法、查表法、电流调节器法等[12]。为实现电流调节器退饱和，可以利用d轴去磁电流抵消永磁体磁场，使电机端电压不超过逆变器电压极限值。由于d轴去磁电流和电机端电压及母线电压有关，因此，通过利用电机端电压和母线电压作为电压环输入，经过PI运算后输出d轴去磁电流，基于电压外环的弱磁控制策略如图5所示。

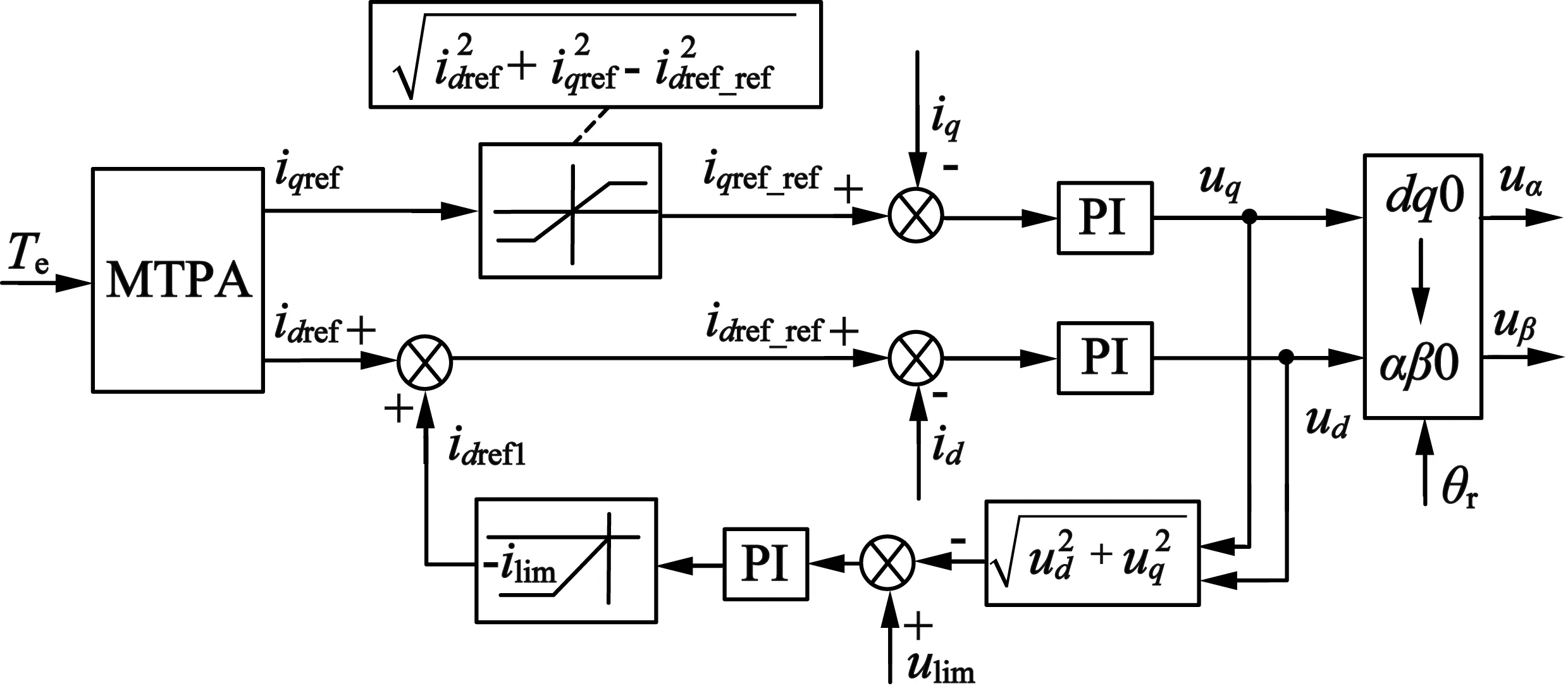
图5 弱磁控制策略框图

图5中，当电机低速运行时，电机端电压低于母线电压，电压外环PI输出限幅值为0，此时电压调节器不起作用，电机运行在恒转矩模式下。当电机运行在高速时，此时电机端电压超过逆变器输出极限值，电压外环起作用，输出去磁电流以抵消永磁体磁场。由于电机相电流受到逆变器限制，因此d轴电流需要限制在最大电流下，对应此时q轴电流进行限幅。最终通过弱磁控制保证电机运行于恒功率模式，电机电压和电流均达到极限值。采用该方法可以最大程度地利用母线电压，由于采用电压外环PI，具有一定的鲁棒性，不需要依赖电机参数。

4 实验结果

4.1 实验平台

为验证采用低分辨率霍尔传感器实现永磁同步电动机矢量控制和电动汽车转矩控制，本文搭建了永磁同步电动机调速系统，如图6所示。该系统主要由蓄电池、STM32F103核心控制板、MOSFET 并联逆变桥、永磁电机和磁粉制动器负载组成。

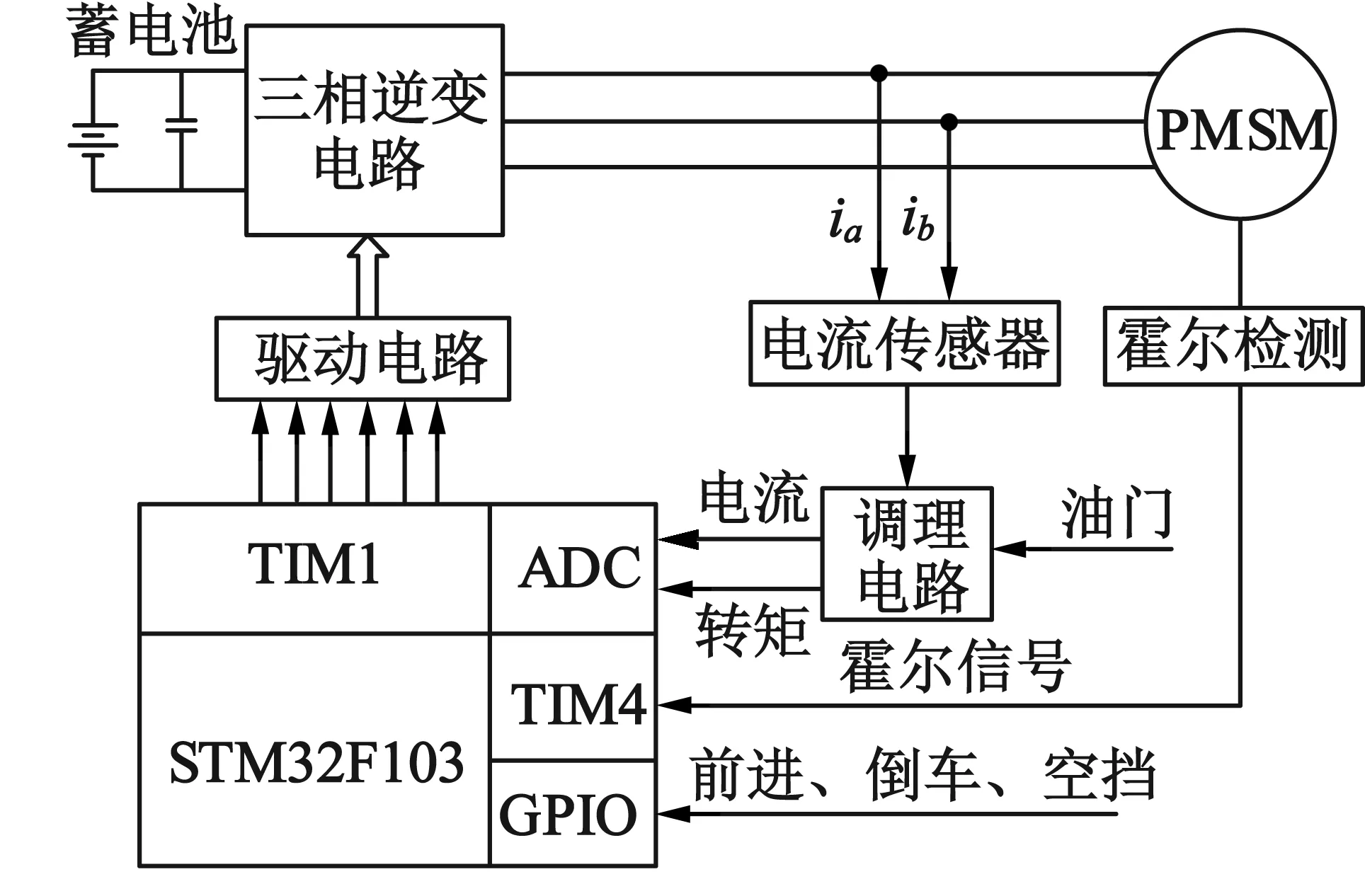
图6 永磁同步电动机调速系统框图

根据电动汽车性能指标要求，本文选择的内置式永磁同步电动机具体参数如表1所示。

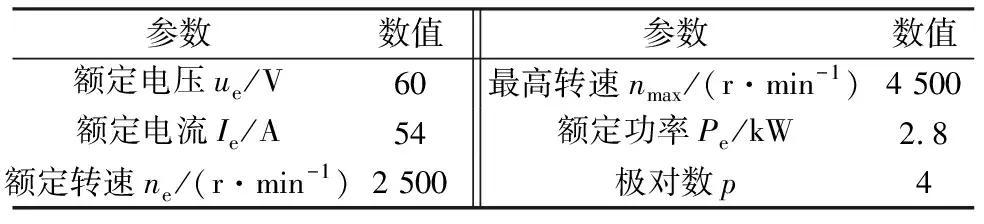
表1 内置式永磁同步电动机主要参数

电机与控制器系统测试平台如图7所示。测试电机经减速器后连接磁粉制动器负载，测试数据利用功率分析仪WT1800和录波仪DL850得到，相关观测变量通过D/A芯片输出。

图7 实验平台示意图

4.2 实验结果与分析

图8为电机逆时针起动阶段实验结果，转子角度采用霍尔状态对应的扇区中间角度，通过减小角度误差以实现负载下电机顺利起动。图9为电机电流和位置角切换过程的实验结果，图9(a)切换点处电流平滑地过渡到正弦波驱动，电流突变较小；图9(b)中转子位置完成从离散切换到连续角度，在霍尔边沿处进行位置校正以消除累计误差。图8和图9实验结果表明，电机可实现负载条件下正常起动和电流切换过程。

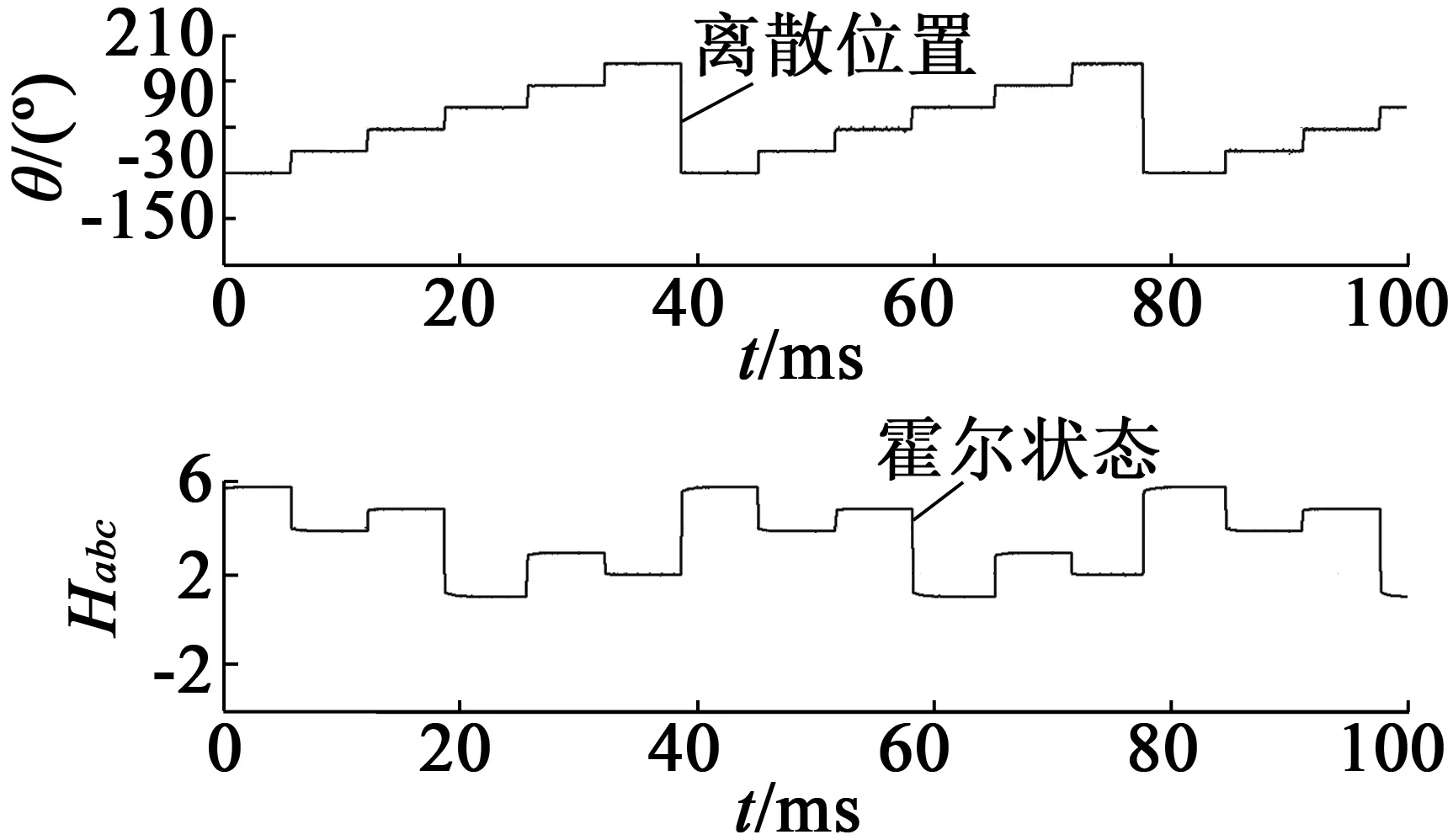
图8 电机逆时针起动时霍尔状态和转子离散角度波形

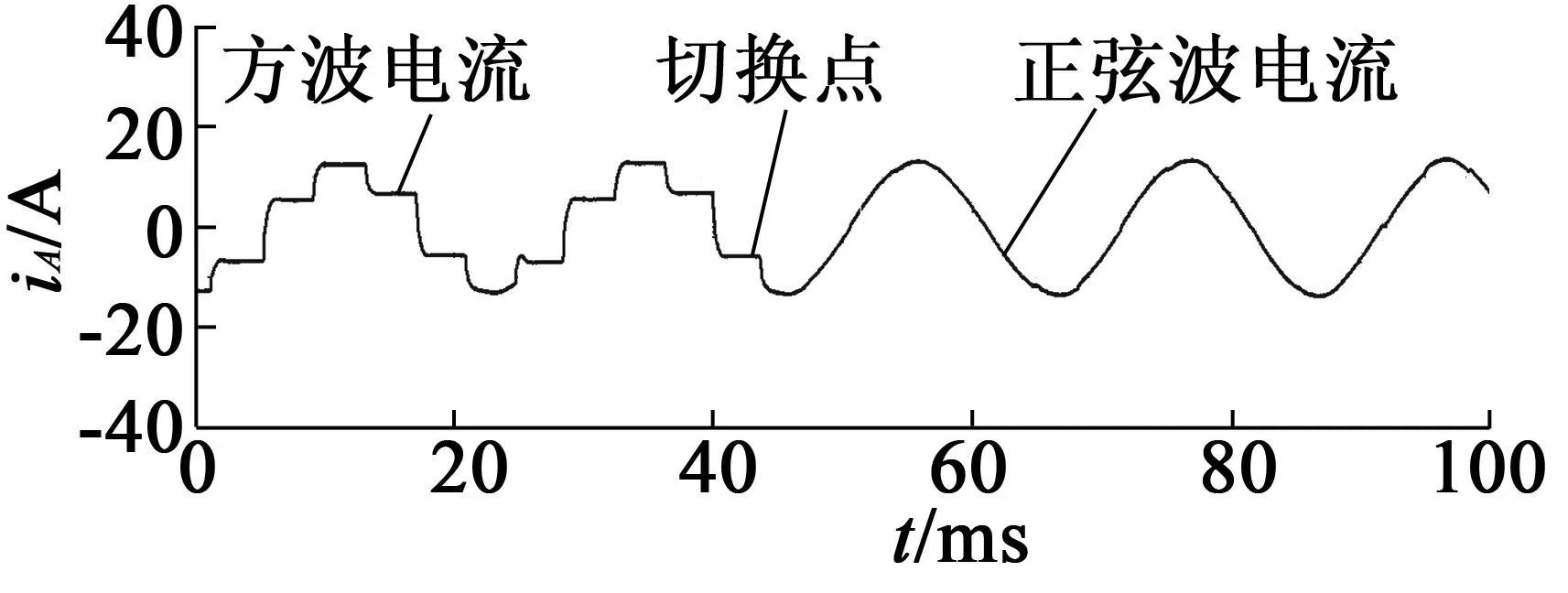
(a) 电流波形

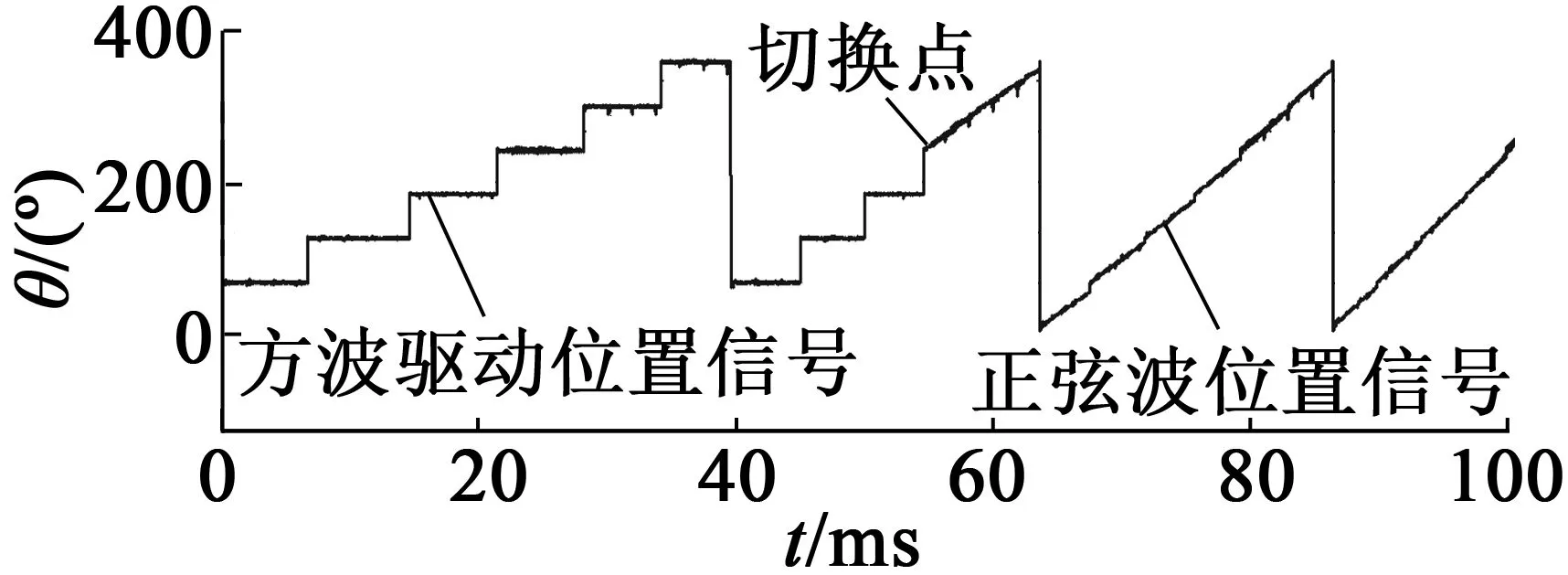
(b) 转子角度波形

额定负载时电机转速突变的动态过程如图10所示。实验过程中指令转速从1000r/min增加到1 800r/min后稳定，最后减小到1 000r/min，负载转矩为额定转矩10.7N·m。

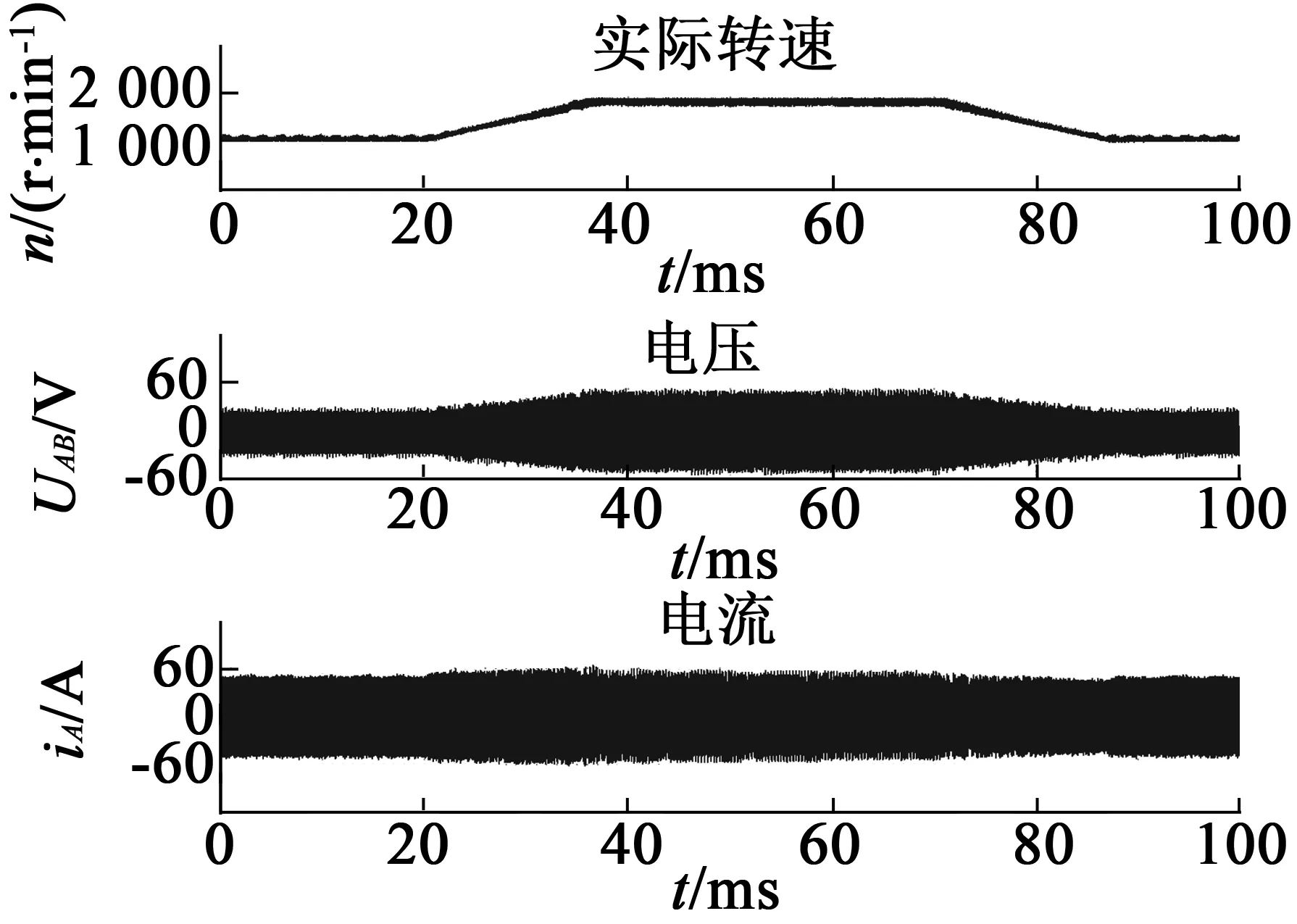
图10 额定负载下电机转速突变的动态过程

由图10可知，满载条件下电机实际转速与给定转速变化过程一致，加速和减速阶段电流突变较小，稳态过程转速误差较小，线电流达到56A，线电压接近60V。实验结果表明，电机转速和转矩动态控制性能较好，电流和电压均控制在设计指标内。

基速以下电机满载运行的测试数据如下表2所示。转速间隔500r/min，利用功率分析仪测量电机相电压、电流和输入功率。

从表2可以看出，电机处于满载情况下，不同转速时相电流有效值基本保持56A不变，相电压有效值和转速成正比增大。基速以下，电机额定点时效率高达91.4%，满足系统要求。

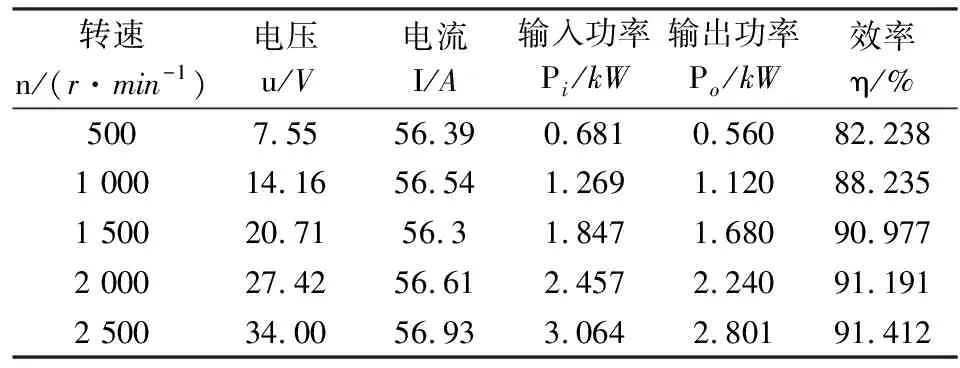
表2 基速以下满载实验数据

为测试电机和驱动器性能，在实验平台上测试恒转矩区域内转矩10.7 N·m，恒功率区域内电机输出功率保持在3 kW的运行点。测试得到电机的稳定运行区域，如图11所示，在2 500 r/min以下为恒转矩控制，2 500 r/min以上为恒功率控制，控制功率保证在3 kW。

图11 永磁同步电动机稳定运行区域

通过测试表明，电机及控制器完全能够满足设计要求，低速时能够输出额定力矩，高速时可以输出高功率达3 kW，最高转速高达4 500 r/min。

图12为电机效率和控制系统效率测试图。电机在低速阶段效率较低，而在中高速电机与控制器效率均可达到90%以上。

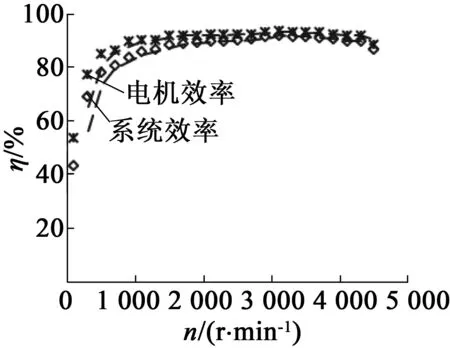
图12 电机效率和控制系统效率测试图

5 结 语

经过理论推导和实验分析得到如下结论：基于霍尔位置传感器的永磁同步电动机可实现电动汽车转矩控制，负载情况下起动时方波和正弦波电流驱动切换过程平缓。采用基于电压外环的弱磁控制可实现电机高速运行，在整个运行区域内电机与控制器具有较高的效率，采用霍尔传感器可以较大地降低系统成本，具有市场竞争意义。