电动汽车用异步电动机定子槽优化设计

董妍男，颜建虎，陈远晟，应展烽，张旭东

(南京理工大学，南京 210094)

0 引 言

电机驱动控制系统作为电动汽车的主要执行机构，是电动汽车的核心部件之一。异步电动机具有结构简单、运行可靠、维护方便等特点，被广泛地运用于低速电动汽车中。但是车用电机狭小的工作空间、频繁的起停与加减速等特点，导致电机温升较大。温升直接影响着电机的寿命和效率等性能以及汽车的安全稳定行驶[1]。因此，国内外众多学者围绕电机温升与损耗优化开展了电机结构参数与控制方面的研究工作。

在电机结构参数优化设计中，大多采用有限元法建立电机模型对其参数进行优化，该方法可以在预优化阶段对模型进行较快的粗优化[2]。目前已有学者用有限元方法就电机定子槽对损耗与温度的影响进行了研究。文献[3]研究了定子槽开口对定子铁心和永磁体功率损耗的影响，研究结果表明定子槽开口会使得定子铁心的磁密整体下降，同时较大的定子槽口也会引起气隙中磁密的变化，导致涡流损耗的增加。文献[4]针对永磁电机建立了有限元仿真模型，在半开式槽和一台全开式槽的电机上进行了有限元计算，结果表明定子槽口在使得定子铁耗降低的同时会导致涡流损耗的增大。文献[5]通过建立轴向磁通永磁样机模型并开展二维负荷性能分析，发现可以通过在开口处引入软磁楔的方法，改善电机的空载性能。文献[6]对小型感应电机进行了二维有限元仿真，通过函数拟合的方法得到了某种型号电机定子槽开口与转子涡流损耗之间的定量变化关系。文献[7]提出了一种考虑了气隙的三相感应电机半解析模型和铁损模型，通过动态分析得出，定子开槽对铁损有着不可忽略的影响。

由于目前对定子槽所引起的损耗研究大多针对永磁同步电机，并且只分析其中某一参数对损耗的影响，未考量各参数的综合影响与参数间的相互影响。为解决上述问题，本文针对低速电动汽车驱动要求，以一台4 kW的异步电动机为例，基于损耗分析与有限元法，建立电机损耗与温度模型，研究了定子槽槽宽、槽口宽以及槽半径对电机损耗与温度的影响，并综合分析了各参数间的相互影响。在保证输出功率、转矩不发生较大变化的前提下，对定子槽尺寸进行优化，达到降低电动汽车电机运行温度的要求。

1 异步电动机有限元计算

1.1 电磁场损耗计算

本文以型号IPQ472，额定功率4 kW的异步电动机为例，基本参数在表1中列出，用Maxwell建立了该电机的二维电磁场模型，如图1所示。

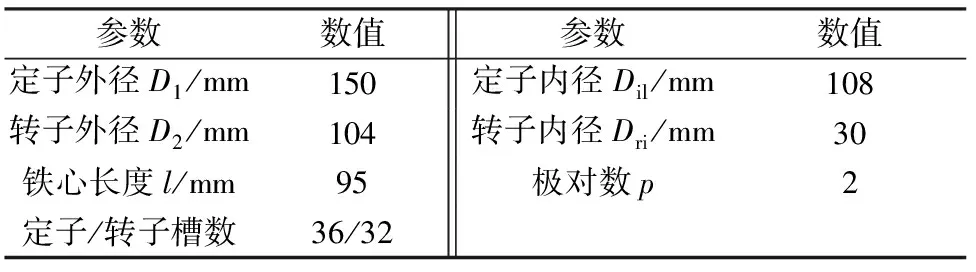
表1 电机基本参数

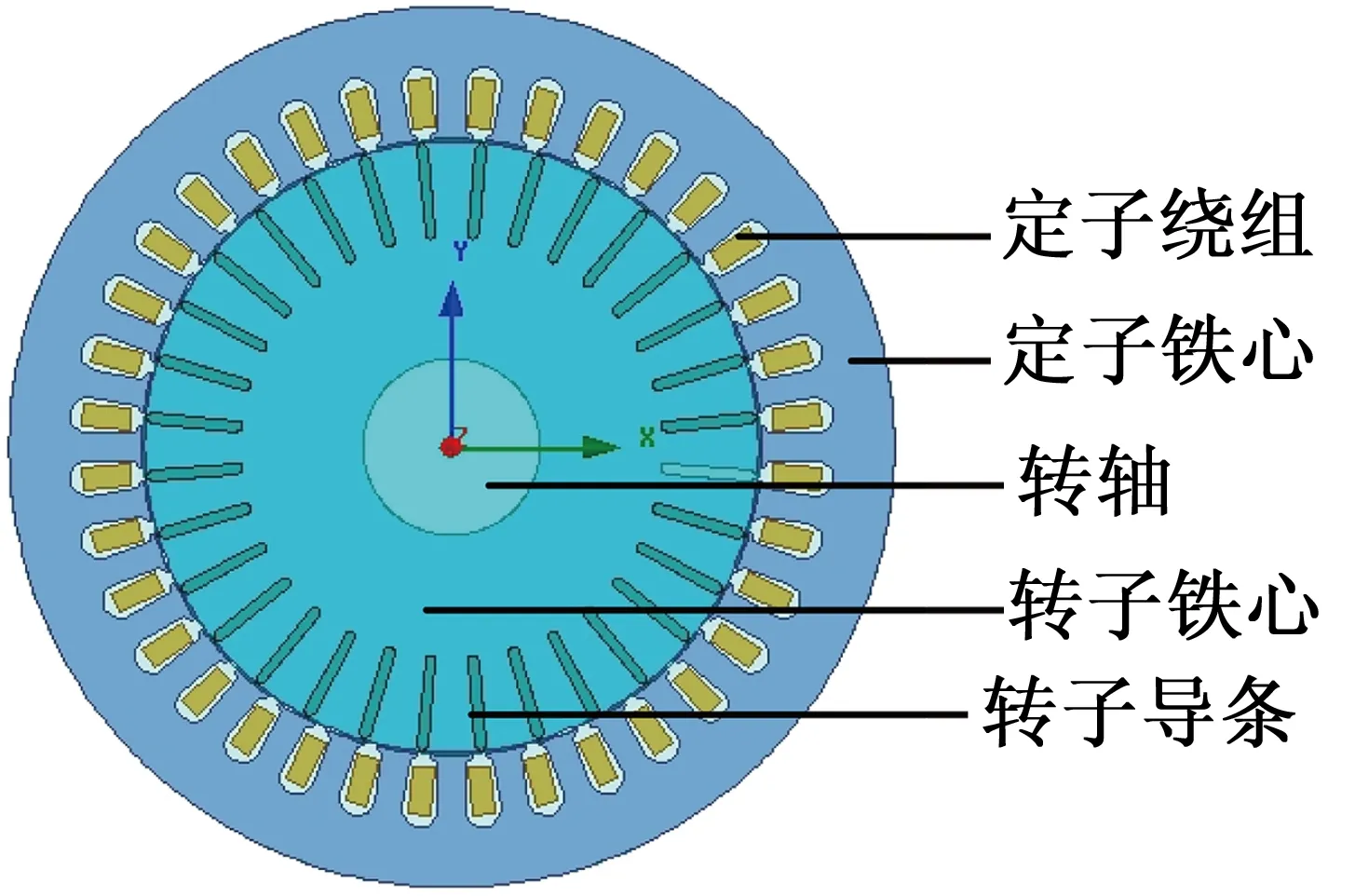
图1 二维电机模型

在电机正常工作时，其损耗可分为铁心损耗、铜耗以及杂散损耗，由于电机的铁耗与铜耗是电机损耗的主要部分[8-9]，因此本文只对铁耗与铜耗进行计算分析。

对于铁耗的计算，国内外学者已提出过多种计算模型与方法[10]，目前普遍认为在交变磁场下铁磁材料的损耗分为磁滞损耗、涡流损耗和异常损耗3部分，总的铁耗计算模型[11]：

(1)

式中：khBαf为磁滞损耗；Bm为磁场幅值；ke,ka分别为与材料相关的涡流和异常损耗系数。

传统的计算定转子铜耗的方法未能将谐波电流的铜耗考虑在内，使用有限元法计算的定子总铜耗[12]：

(2)

式中：pscu为定子总铜耗；Rs为定子相电阻；ivA,ivB和ivC为三相绕组的各频次电流，v为谐波次数，v =2k+1(k=0,1,2,3，…)，v =1时表示基波。

考虑集肤效应，转子铜耗的有限元计算式[12]：

(3)

式中：pRcu为转子总铜耗；σ为导条电导率；Lef为导条有效部分的长度；Sn为有限元各单元面积；Jnv为包括基频在内的各频次电流密度有效值。

1.2 温度场计算

用ANSYSWorkbench建立电机三维温度场模型，由于电机在稳态运行时几何结构与损耗分布的对称性[13]，建模时取轴向的一半并取定子转子各一槽作为简化计算模型，如图2所示。

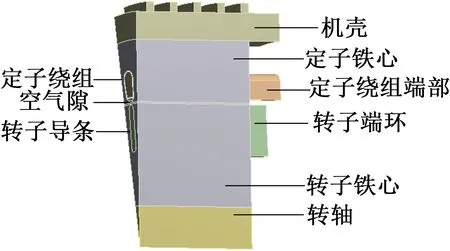
图2 三维电机物理模型

在三维温度计算过程中，为简化计算，作如下假设[14]：(1) 全部损耗以热量的形式从机壳表面散出；(2) 气隙与电机内端部空气温度均匀；(3) 导热系数随温度的变化可忽略。

将电机运行中产生的损耗作为热源，分别施加到定子绕组、转子导条、铁心等部分，来计算电机运行达到稳态时的温度分布，首先要确定气隙的导热系数与电机表面的散热系数。

电机气隙内的空气运动过程，一般采用经验公式，引用等效导热系数的概念[15-16]，将转子看作静止处理，气隙中的空气等价为静止空气，则等效导热系数[17-18]可以用下式计算。

气隙雷诺数：

(4)

式中：g为气隙厚度；ν为空气运动粘度系数。

临界雷诺数：

(5)

式中：Di1为定子铁心内径。

气隙中的空气流动为层流时(RegRecr)，气隙等效传热系数λg计算如下：

(6)

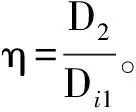
电机运行过程中处于封闭空间，机壳表面为强制对流，对流换热系数[19]：

(7)

式中：v1为机壳表面空气流动速度。

定子铁心端部散热系数：

(8)

式中：vr1为转子表面线速度。

定子绕组端部对流换热系数αet[16]：

(9)

(10)

(11)

(12)

式中：Nuet为定子绕组端面的努塞尔数；λa为空气的热传导系数。

转子铁心端部对流换热系数[16]：

(13)

(14)

(15)

式中：Nur为转子铁心端部努塞尔数。

考虑上述导热系数，忽略各部分间的接触热阻，按照上文方法计算，将损耗当作热源，代入三维模型中，即可得到电机运行时的温度分布。

2 不同槽形尺寸对温度影响的分析

本文电机采用梨形槽，如图3所示，其基本尺寸主要包括槽口宽度b01、槽口高度h01、槽高h12、槽宽bs1、槽肩角α、槽半径Rs。槽形尺寸如下：b01=2.24mm，h01=0.47mm，h12=8.945mm，bs1=4.53mm，α=30.15°，Rs=3mm。

由文献[20]可知，槽口高度、槽肩角、槽高对电机损耗的影响程度较小，在优化过程中调整其数值对其他参数的影响也较小，故本文主要研究槽口宽度、槽宽以及槽半径对电机温度的影响，同时考量在槽面积固定的情况下各参数间的相互影响，以便优化电机的结构参数。

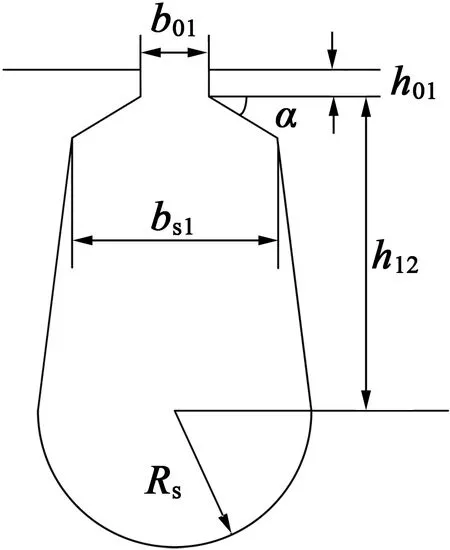
图3 梨形槽基本槽型尺寸

2.1 槽口宽度的影响

将定子槽口宽度分别设置为2.04mm,2.14mm,2.24mm,2.34mm,2.44mm，调整槽口高度、槽肩角、槽高，以保证槽面积无较大变化，在电机空载情况下分别计算损耗与温度分布，结果如表2所示。

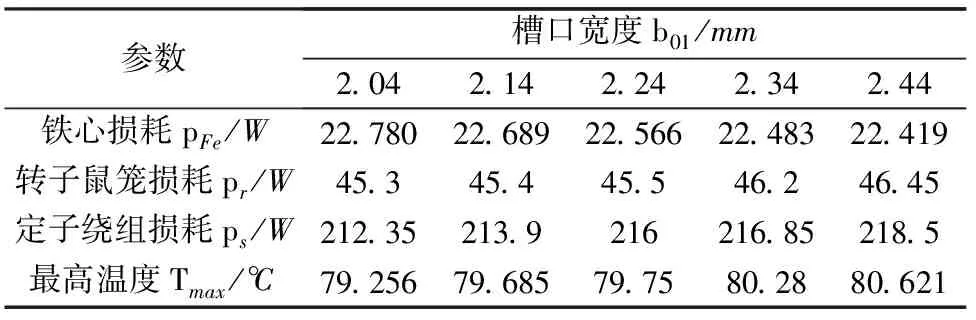
表2 槽口宽度对空载损耗的影响

可以看出，随着定子槽口的增大，电机的温度不断升高。这是由于随着槽口宽度的增大，转子齿中的脉振损耗增大，同时转子齿中的磁通脉动增大，导致在转子导条中形成涡流，从而产生转子空载铜耗，槽口宽度越大，这种损耗就越大。

2.2 槽宽的影响

仿真中槽宽的取值分别为4.33mm，4.43mm，4.53mm，4.63mm，4.73mm，同样保持槽面积的基本一致，在空载情况下算得其温度分布,如表3所示。

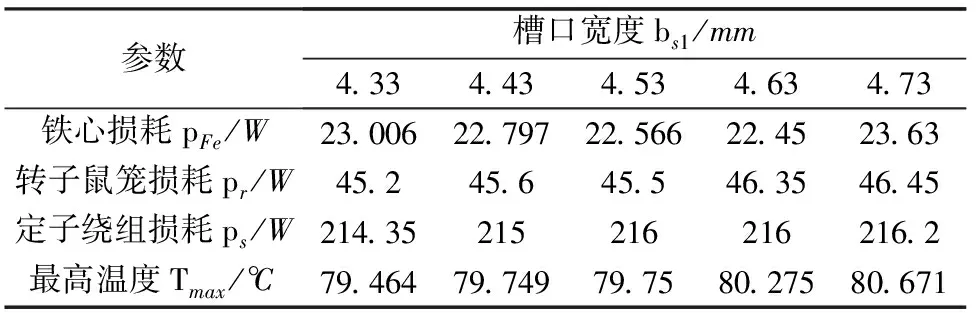
表3 槽宽对空载损耗的影响

由表3可得，温度随槽宽的增加而升高。这是因为定子齿部宽度的减小，使得磁路饱和程度与损耗均增大，所以温度上升。

2.3 槽半径的影响

槽半径分别设置为2.9mm，2.95mm，3mm，3.05mm，3.1mm，按照上述条件计算温度分布,如表4所示。

表4 槽半径对空载损耗的影响

随着槽半径的不断增大，轭部磁路面积减小，饱和程度增加，损耗增大，故温度不断上升，且槽半径的大小对槽面积影响较大，在选择尺寸时变化不宜过大。

根据表2～表4数据得到如图4所示的温度随参数变化曲线。可看出，不同尺寸变化程度与温度变化程度的关系。作为对温度影响较大的3个参数，在一定的变化范围内，槽半径和槽宽对温度的影响程度相对较大，但是在保证槽面积不变的情况下，槽半径和槽宽对其他尺寸参数的影响也较大。所以在优化定子槽参数时，在保证槽满率不发生较大变化的情况下，小程度调整槽半径、槽宽，重点调整槽口宽度，同时对槽口高度、槽肩角、槽高等参数略微调整，使电机温升得到一定程度的优化。

3 定子槽的优化

根据上述所得结论对定子槽尺寸进行优化，以达到降温的目的。为了使得电机在优化后仍适用于大规模传统工艺生产，各尺寸调整需要考虑以下几个方面：

(1) 槽口尺寸合理，以便加工时嵌线；

(2) 优化后的定子铁心齿部机械强度与轭部刚度基本不变；

(3) 优化后的槽满率不宜过高；

(4) 适当调整气隙长度，减小谐波漏抗，使得总漏抗，基本不变，确保起动性能。

在满足上述条件的情况下对槽的尺寸进行优化，得到的槽形尺寸如表5所示。

表5 优化前后尺寸对比

按照式(18)计算优化后的槽满率为71.2%，与优化前的70.1%相比，没有明显增加加工难度。

(16)

式中：N为导线并联根数；Zn为每槽导线数；S为选用导线的截面积；An为槽面积。

考量优化前后电机的起动性能与输出功率，额定工况下起动转矩最大的瞬时值分别为20.47 N·m和20.41 N·m，由此可见，优化后电机原有的起动性能未受到影响。

表6为额定工况运行时，优化前后各项损耗的对比数据。可以看出，总损耗下降了6.17 W，由于定子槽尺寸的改变，使得齿部饱和程度降低，并且槽口变窄会使谐波电流减小，从而使铜耗降低。如图5所示，优化后磁密有小幅上升，故铁心损耗有所升高，但升幅较小，电机整体损耗下降。

表6 优化前后满载损耗对比

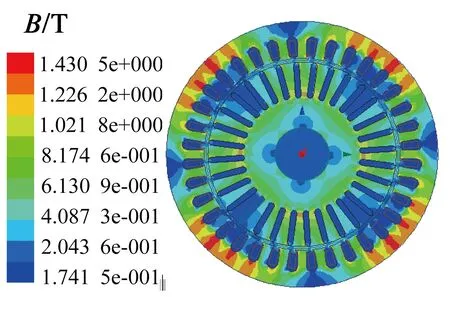
(a) 优化前磁密分布

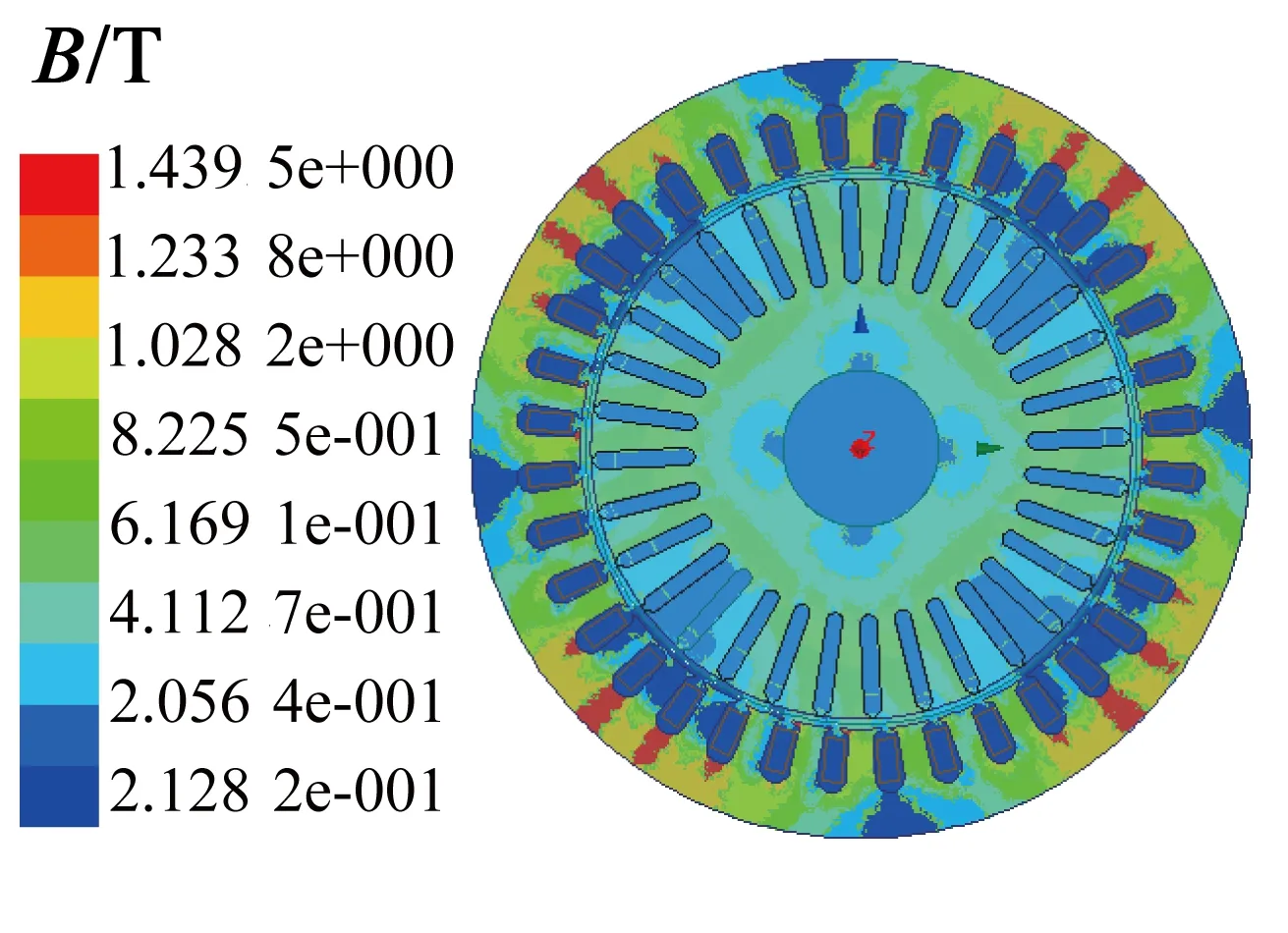
(b) 优化后磁密分布

考虑到研究的实用性，按照理论模型计算优化前后电机在额定工况下的温度分布，如图6所示。与原电机相比，优化后电机的最高温度下降了1.3%。

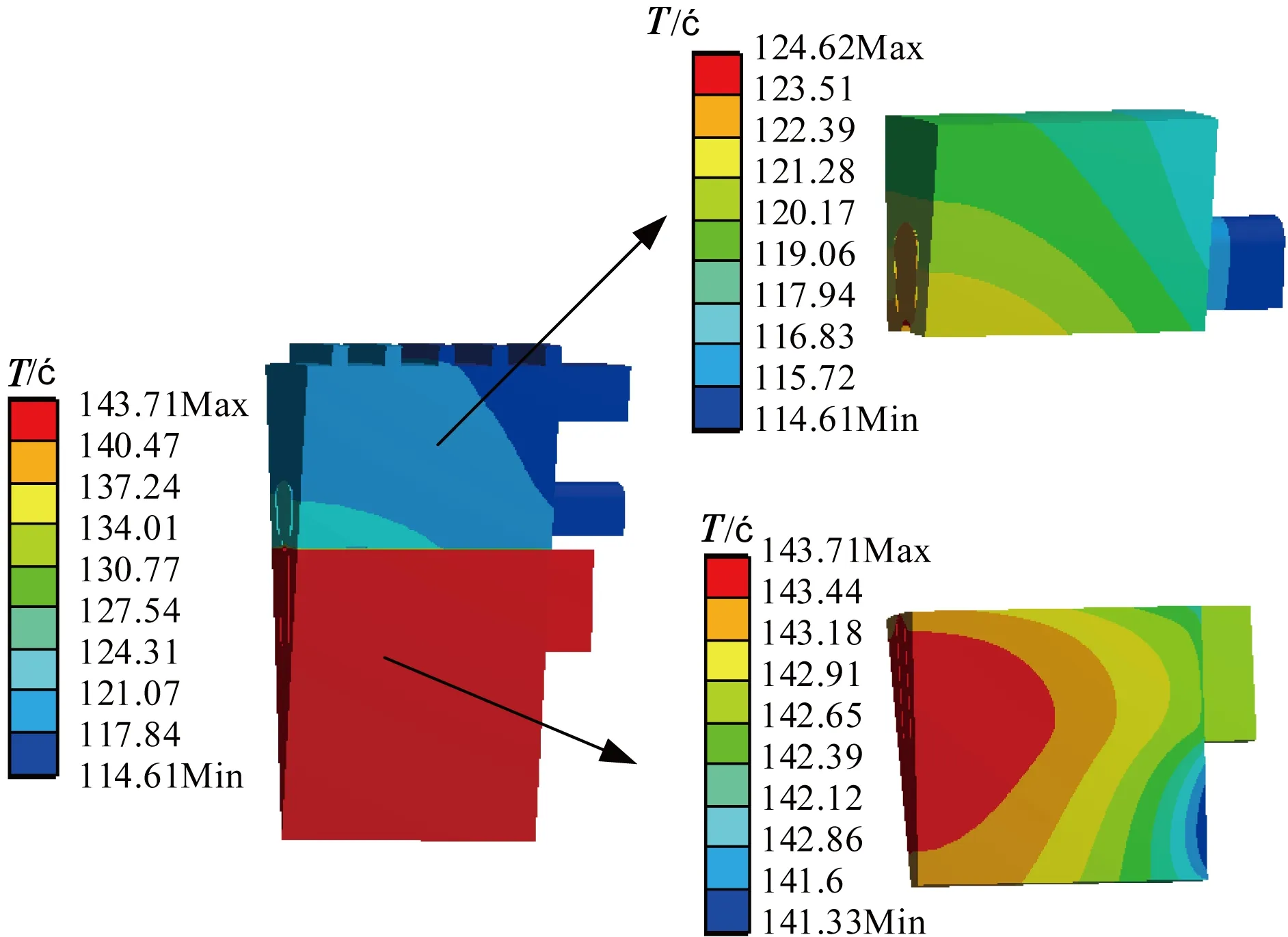
(a) 优化前温度分布

(b) 优化后温度分布

4 结 语

本文以一台2对极4 kW的电动汽车用异步电动机为例，围绕其损耗与温度展开了研究。首先建立了二维电磁场模型，分析了损耗产生的主要原因，总结了计算损耗的方法公式；然后建立三维温度场模型，利用有限元方法求解了额定工况下的温度场分布，并分析了不同定子槽参数对温度分布的影响程度；最后根据分析结果对定子槽各参数进行优化，得出下述结论：

1) 电机在运行过程中转子的温度是最高的，这是因为转子材料良好的导热性，其温度在各区域内基本不变。而转子与定子的较大温度差异主要由气隙的不良散热环境导致。

2) 槽半径、槽宽与槽口宽度均对电机的温度有较大的影响，但是在一定范围内，槽口宽度变化导致温度发生较显著变化的同时，对其他参数的影响较小，而槽半径与槽宽虽可使温度降低，但也使其他参数发生了较大变化，影响槽满率。

3) 为降低电机运行温度，对定子槽参数优化时，在槽面积一定的条件下适当调整槽口宽度、槽宽与槽半径，同时对槽口高度、槽肩角与槽高做相应调整。

4) 本文对电机模型所做的定子槽参数优化，可有效降低电机损耗与运行温度，同时不影响原有的运行性能。