一种基于PWM的音圈电机改进控制方法

周 平，吕 勇，夏润秋，王德钊

(北京信息科技大学，北京 100192)

0 引 言

音圈电机是单相两极装置，是一种通过安培力驱动的线性运动电机[1-3]，具有结构简单、响应快、运动精度高等特性[4]。随着对高速、高精度定位系统性能要求的提高，以及音圈电机技术的迅速发展，音圈电机被广泛用于高速、高精度系统中，例如高档数控机床、光学电子显微镜[5]、医学装置中精密电子管及光学系统中透镜定位等。

音圈电机的驱动方式有2种，一种是直接通过线性功率放大器驱动，它的不足之处在于线性功率放大器驱动音圈电机工作时器件功耗大，尤其在密闭的环境中散热成为问题，小功率音圈电机常用这种驱动方式[6]；另一种驱动方式为开关型脉宽宽度调制式(以下简称PWM)，PWM稳压电路是在控制电路输出频率不变的情况下，通过电压反馈调整其占空比，从而达到稳定输出电压的目的。它具有实现容易、控制简单、动态响应好、控制精度高等优点[7]，PWM驱动音圈电机方式广泛应用于自动控制系统中。文献[8]采用PWM驱动音圈电机的方式控制快速反射镜系统，系统带宽达到150 Hz以上；文献[9]利用PWM设计了基于音圈电机的直驱阀阀心位置控制系统等。由于音圈电机在高速精密定位控制中存在多种非线性因素，如摩擦力、死区和迟滞特性等[10]，当输入的PWM信号占空比较小时，PWM信号驱动的音圈电机运动效率较低，系统无法获得理想的动态特性，直接采用传统的闭环控制算法难以满足高动态特性要求。目前国内外对低占空比PWM信号驱动音圈电机的特性研究较少,本文提出一种改进闭环控制算法，降低由于PWM驱动信号占空比减小对音圈电机动态特性带来的影响，并将该算法应用于高速精密光束指向系统。

1 PWM信号驱动的音圈电机工作特性

音圈电机在高频高速运动中具有非线性的复杂特性，尤其带负载运动时，存在动静摩擦力[11]。高频率运动下，音圈电机中的磁体电流、摩擦力和重力场等非线性因素严重影响着音圈电机的执行效率[12]，而小占空比PWM信号产生的驱动电流较小，不足以驱动音圈电机克服上述阻尼实现线性运动，PWM信号驱动音圈电机未发生任何位移的占空比范围为PWM占空比“控制死区”。

为了准确了解音圈电机在不同占空比PWM信号驱动下的工作特性，以某款音圈电机为例，开环状态下，给定音圈电机不同占空比的PWM信号，获取了音圈电机归一化行程与PWM信号占空比之间的关系。测试结果如图1所示，其中音圈电机行程的正负表示音圈电机移动的方向，音圈电机为“1”表示音圈电机满量程，为“0”表示音圈电机处于初始位置。

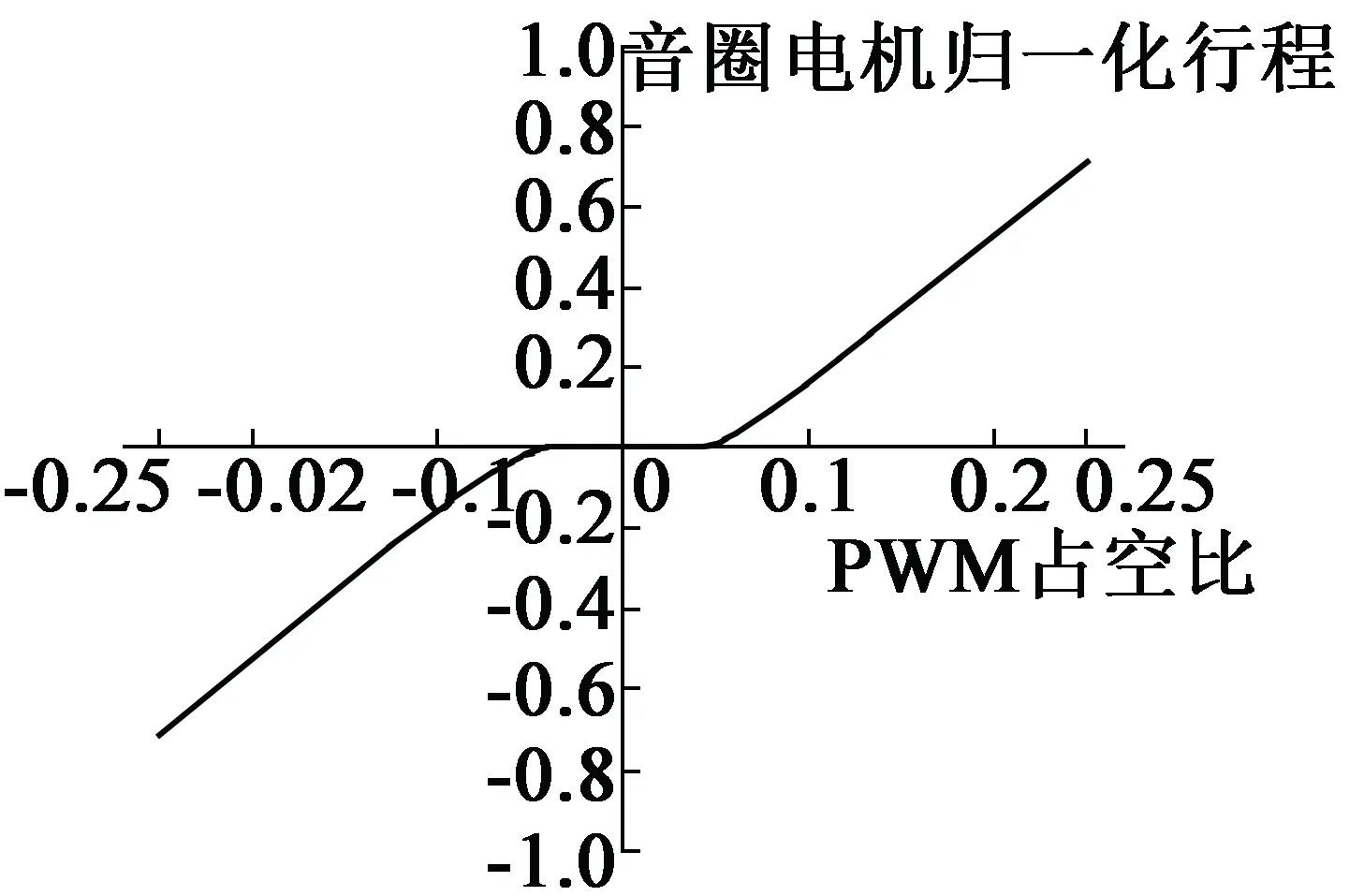
图1 PWM占空比与音圈电机位移关系

由图1可以看出，开环状态下，PWM占空比在-0.05～0.05范围内，音圈电机未发生任何位移，该段即为PWM占空比“控制死区”。在该范围外，音圈电机的位移量随着PWM占空比的增加呈线性变化。在PWM占空比“控制死区”内，由于音圈电机不能产生任何响应，PWM驱动的音圈电机伺服系统利用常规PID控制算法不能达到快速精确的性能要求。

2 改进双闭环控制算法原理

在电机控制中，双闭环控制算法基于经典PID控制算法的思想实现，一般由电流环和电压环构成[13-17]，或由电流环和速度环组成[18-19]。其中电流环作为内环，通过控制电流来提高系统的性能；电压环或速度环作为外环，控制系统精确达到目标位置。双闭环算法使得系统性能得到较大提高。但由于电流环和位置环均需要独立的反馈装置，增强了系统设计的复杂性。本文提出一种改进双闭环控制算法，用于应对PWM占空比“控制死区”缺陷。改进双闭环控制算法的结构如图2所示。 该算法采用位置环和速度环相结合的方式，通过位置环实现对音圈电机伺服系统位置控制；速度环反馈量与位置偏差量相关，根据音圈电机移动速度的大小实现对位置环中PID算法积分环节控制。

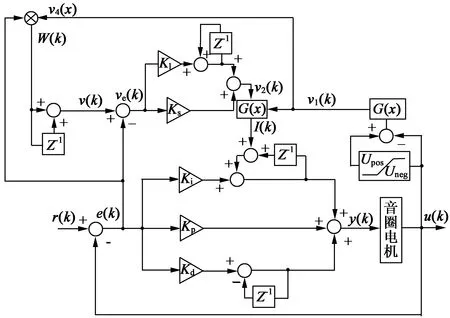
图2 改进双闭环控制算法结构图

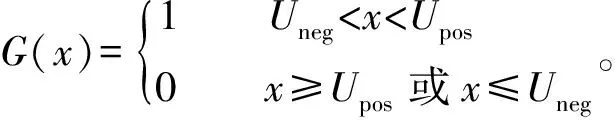
改进双闭环控制算法位置环的输入变量为期望值r(k)与输出值u(k)之间产生偏差信号e(k)，位置PID控制器根据偏差信号e(k)计算输出值y(k)，进而将输出值y(k)对应的PWM占空比驱动音圈电机产生偏移。其中位置PID控制器公式[20]：

(1)

同时，产生的偏差信号e(k)与期望的速度v(k)做差分，产生速度偏差信号ve(k),并根据测试占空比死区对应的音圈电机位移范围[UnegUpos]，判断音圈电机当前位置是否处于占空比死区范围内，如果处于该范围内，G(x)的值为1，输出信号v(k)为1，I(k)为v2(k)与v1(k)的乘积，W(k)为e(k)与v4(k)的乘积，则将速度偏差信号作为速度环的输入信号，并将计算后输出结果M叠加在位置PID控制器上，从而实现双闭环控制。其中期望速度v(k)根据音圈电机位置位于[UnegUpos]范围临界区前一时刻速度v(k-1)确定,并在[UnegUpos]范围内保持该速度不变；超出该范围后，G(x)的值为0，速度环控制失效。v(k)取值如下：

(2)

速度环输出结果M的取值如下：

(3)

式中：Ks为速度环中比例系数；KI为“速度环中积分系数。则整个控制器输出表达式：

(4)

改进双闭环算法的流程图如图3所示。

改进双闭环算法降低了系统设计的复杂性，同时该算法对于占空比死区范围外部分，速度环作用消失，不影响位置环PID控制参数，使得控制算法中各项参数能够独立调节，参数整定容易。

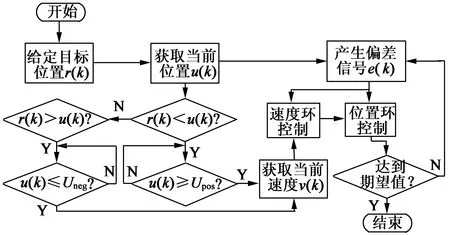
图3 改进双闭环算法流程图

3 实验验证

搭建高速精密光束指向系统，系统结构如图4所示，由两两相互对称的4个音圈电机通过柔性铰链连接反射镜组成。音圈电机采用推拉的方式控制反射镜偏转到指定角度。其中沿竖直方向对称的一组音圈电机控制反射镜沿x轴方向移动，水平方向对称的一组音圈电机控制反射镜沿y轴方向移动。通过2组音圈电机相互作用，系统可以偏转到任意方向指定的角度。

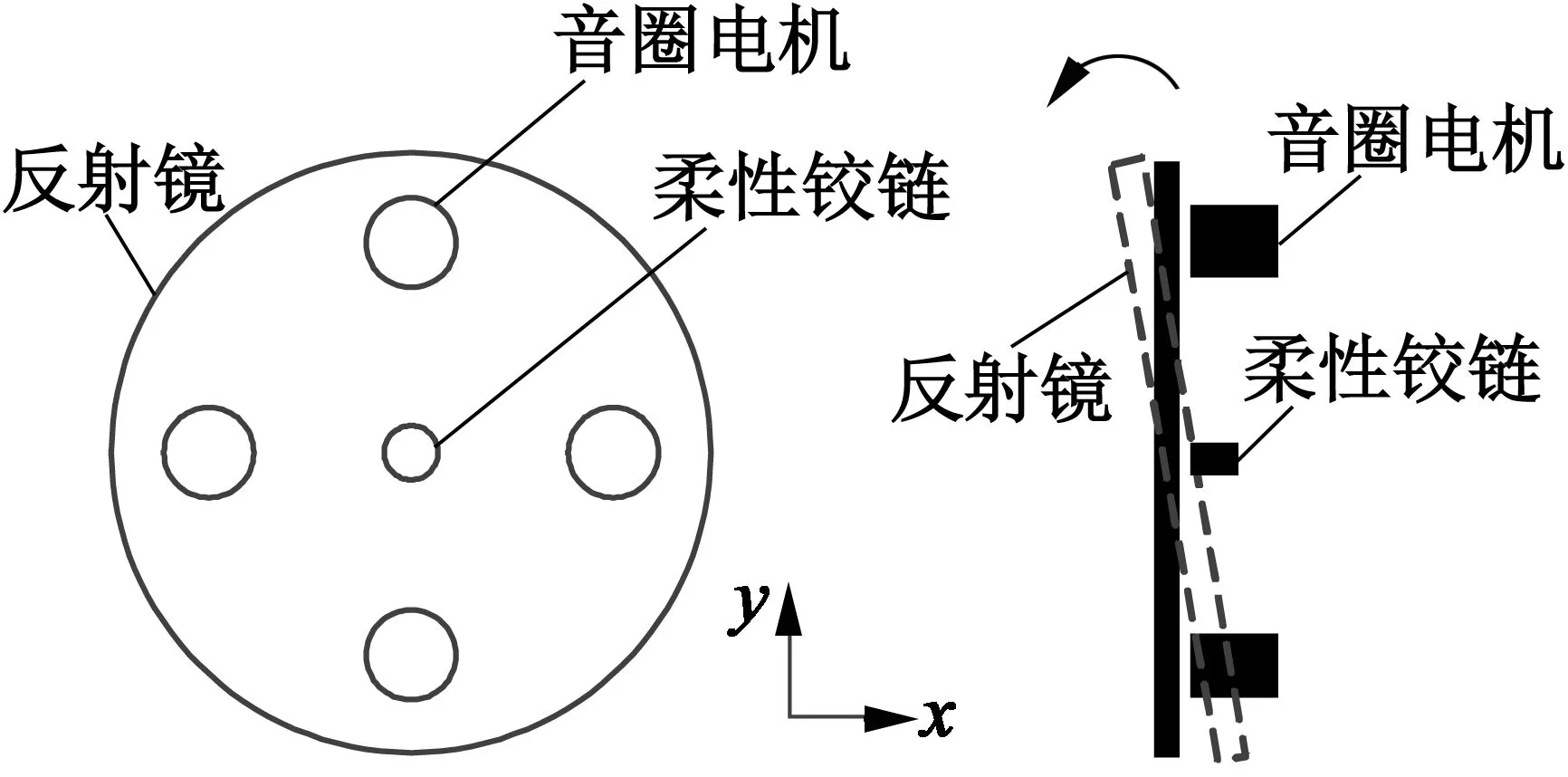
图4 高速精密光束指向系统结构图

将改进双闭环控制算法和常规算法分别应用于该系统中，分别调整改进双闭环控制算法和常规算法中的各项参数，并给定系统阶跃信号，使得PWM信号占空比变化区间包含占空比“控制死区”，获取了2种算法阶跃响应控制曲线，如图5所示。

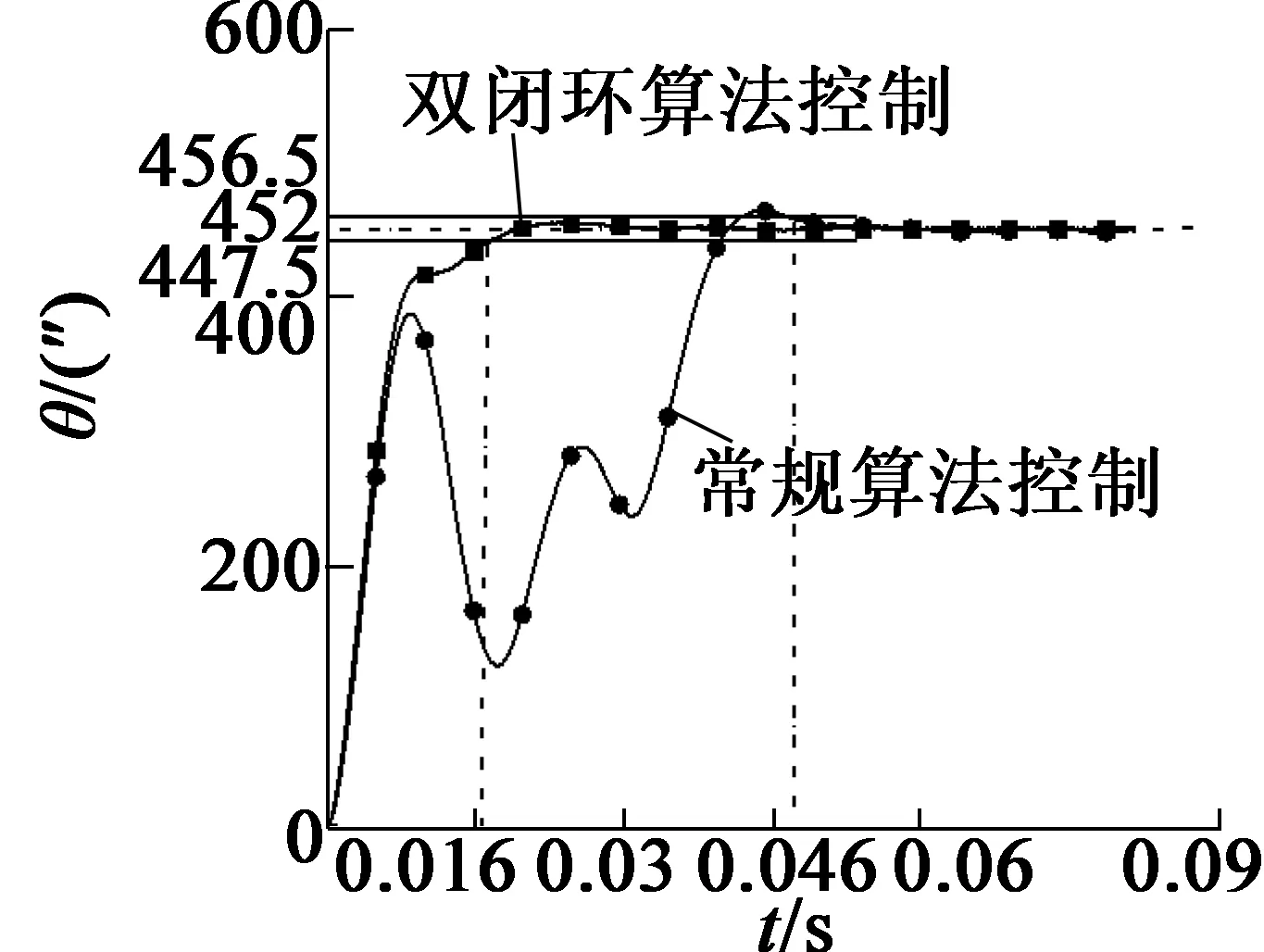
图5 改进双闭环算法和常规算法阶跃响应曲线

图5以时间为横轴，高速精密光束指向系统偏移角度为纵轴绘制曲线。从图5可以看出，在系统稳态误差1%允许范围内，常规PID控制算法控制的系统产生阶跃响应调节时间为0.046 s，控制时间较长，且系统振荡严重，动态性能较差，控制效果不理想。改进双闭环算法控制的系统调节时间为0.016 s，将系统的调节时间缩短了约65%；同时系统控制过程中振荡也得到较大的削弱。由此可见，改进双闭环算法提高了高速精密光束指向系统的动态性能，在经过占空比“控制死区”时的控制性能优于常规PID算法的控制性能。

4 结 语

本文结合PWM驱动音圈电机线性运动的特性，针对PWM控制的音圈电机存在占空比死区问题，提出了改进双闭环控制算法，并将该算法应用于高速精密光束指向系统。当音圈电机位置处于占空比“死区”时，该算法不仅降低了该“死区”对整个控制回路的影响，将系统的调节时间缩短了约65%，还使系统在死区范围内振荡得到削弱，提高了系统的稳定性。

改进双闭环控制算法不仅适用于高速精密光束指向系统，同时还可以用于PWM控制的其他伺服控制系统中，不但能提高控制系统的动态响应特性，还增强了系统的鲁棒性。