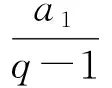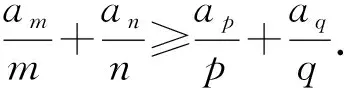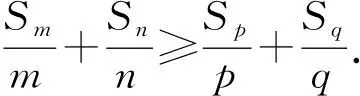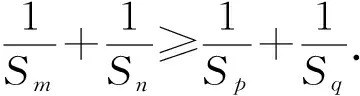由省赛题谈数列“凸性”的简单应用*
●
(严州中学新安江校区,浙江 建德 311600)
2018年浙江省高中数学竞赛已经落幕,纵观全卷,难度较2017年明显下降.笔者对第13题的数列不等式题产生了兴趣.

(2018年浙江省高中数学竞赛试题第13题)
1 证法探究
本题的证明并不难,参考答案提供的是反证法,证法如下:

1)若x1 009,x1 010同为正数,由xn,xn+2同号可知:x1,x2,…,x2 018同为正.
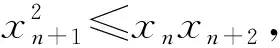
从而
即
x1 009x1 010≤x1 011x1 008,
于是
x1 011x1 008>1.
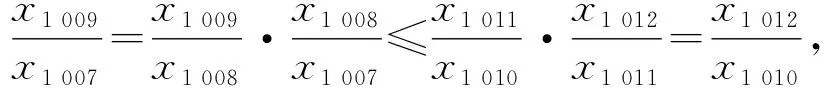
即
x1 007x1 012>1,

2)若x1 009,x1 010同为负数,由xn,xn+2同号可知:x1,x2,…,x2 018都为负数,故
即
由情形1)知不等式成立.
赛后跟学生交流,发现学生的想法也很不错,笔者略作整理,得到如下两种证法:

1)若x1 009·x1 010<0,则结论显然成立.
2)若x1 009·x1 010>0,则x1,x2,…,x2 018全同号,不妨设全为正数(若为负数,则可用-xi代替xi,不影响结果).
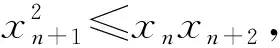
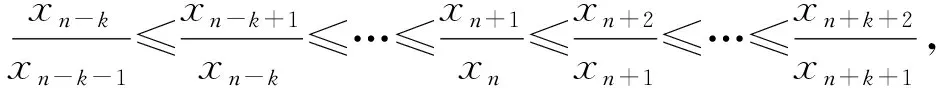
从而xn+k+1xn-k≤xn+k+2xn-k-1(其中0≤k≤n).
取n=1 009,得
x1 009x1 010≤x1 008x1 011≤x1 007x1 012≤…≤x1x2 018,
从而
即
x1 009x1 010≤1.

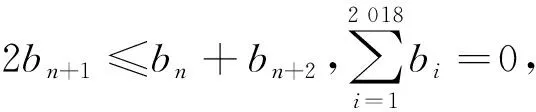
bn+2-bn+1≥bn+1-bn,
即数列{bn+1-bn}单调不减,则
其中k=1,2,…,1 009,即
b1 009+b1 010≤bk+b2 019-k,
对k求和得
即
故
b1 009+b1 010≤0.
2 题源探究
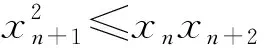
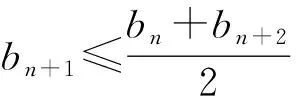
定义若实数列{an}满足ak-1+ak+1≥2ak(其中k=1,2,…),则称数列{an}为下凸数列,简称凸数列,当且仅当{an}为等差数列时,等号对所有k∈N*成立.
由定义可知,对于实数列{an},若Δan=an+1-an(其中n=0,1,2,…),则数列{an}为凸数列的充要条件是数列{Δan}为单调不减数列.
因为等差数列是特殊的凸数列,那么一般的凸数列是否具备类似等差数列的性质呢?从证法3可得到凸数列的一个重要性质:
性质1若数列{an}为凸数列,满足1≤m 证明因为n>q≥p>m≥1,又{an+1-an}单调不减,所以 即 an-aq≥ap-am, 结论成立. 此外还有一些类似等差数列的性质,在此不再一一例举.在一些大型的考试中,也屡见凸数列的“身影”,下面试举两例来说明. 真题1设实数x1,x2,…,x30满足x1=1,x30=88,2xn+1≤xn+xn+2(其中n=1,2,…,28),求x10的最大可能值. (2018年中国女子数学奥林匹克浙江省选拔试题第3题) 解由题意知数列{xn}为凸数列,故{xn+1-xn}是单调不减数列,令Δxn=xn+1-xn,则 Δx1≤Δx2≤…≤Δx29, 且 Δx1+Δx2+…+Δx29=87, 即 Δx1+Δx2+…+Δx9≤27, 故 x10=x1+(Δx1+Δx2+…+Δx9)≤28. (2008年上海市春季数学高考试题第21题) 证明易知 bn=(1,an+1-an)·(0,1)=an+1-an, bn+1=an+2-an+1, 因为bn+1>bn,所以 an+2-an+1>an+1-an, 即数列{an}为“下凸数列”.要证 即证 aq-ap>an-am. 由于q-p=n-m,将所证不等式改写为 由{an+1-an}的递增性,知结论显然成立. 在研究完两个真题后,笔者感到意犹未尽,在翻阅文献时,发现在文献[1]中给出等差、等比数列的一些统一性质,其论证过程比较麻烦.经过尝试,笔者发现若利用凸数列的性质来证明,可以极大地简化证明过程. 性质2正项等差数列或等比数列{an}中,当m+n=p+q,m 证明1)若{an}为等比数列,则显然有 aman=apaq. 2)若{an}为正项等差数列,设an=pn+q(其中p>0),则令bn=-lnan,考虑 f(x)=-ln (px+q)(其中x>0), p,q为常数,则 从而f(x)为凸函数,故数列{bn}是凸数列,则 bm+bn≥bp+bq, 即 -lnam-lnan≥-lnap-lnaq, 亦即 aman≤apaq. 性质3正项等差数列或等比数列{an}中,当m+n=p+q,m 证明1)若{an}为等差数列,则显然有 am+an=ap+aq. 2)若{an}为正项等比数列,设an=a1qn-1(其中a1>0,q>0),显然数列{a1qn-1}是凸数列,则am+an≥ap+aq. 性质4设正项等差数列或等比数列的前n项和为Sn,则当m+n=p+q,m 从而f(x)为凸函数,故数列{-lnSn}是凸数列,于是 -lnSm-lnSn≥-lnSp-lnSq, 即 SmSn≤SpSq. 则 从而f(x)为凸函数,故{-lnSn}是凸数列,即 -lnSm-lnSn≥-lnSp-lnSq, 于是 SmSn≤SpSq. 性质5设正项等差数列或递增等比数列的前n项和为Sn,则当m+n=p+q,m 2)若{an}为正项等比数列且q=1,则显然有 Sm+Sn=Sp+Sq. 此外通过性质2~5的证明,笔者还发现了与凸数列有关的等差、等比的其他一些性质: 由于性质6~8的证明过程和性质1~5类似,故在此不再赘述.在性质2~8中对于等差、等比数列还有一定的限制,那么对于更一般的等差、等比数列,上述性质还成立吗?由于笔者能力有限,未能给出结果,请同行帮忙证明.3 用“凸性”研究真题
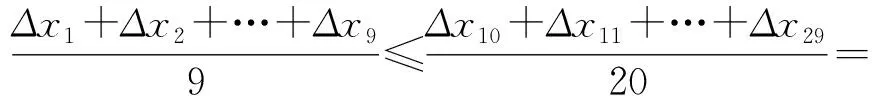
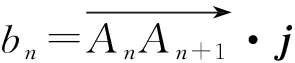
4 由“凸性”研究等差、等比数列的统一性质