一题多维“细”探究 零点反思“化”归根*
——一道高考函数压轴题的解法探究与反思
●
(天水市第一中学,甘肃 天水 741000)
1 试题呈现
题目已知函数f(x)=ex-ax2.
1)若a=1,证明:当x≥0时,f(x)≥1;
2)若f(x)在(0,+∞)上只有一个零点,求a.
(2018年全国数学高考卷Ⅱ理科试题第21题)
2 表征解读
本题条件只是一个含e的函数解析式,蕴藏着一个参数a和两类基本函数(指数函数和二次函数),第1)小题属于不等式的证明;第2)小题通过零点求参数,结构与形式凸显了数学之美:简单、简洁、简捷.结构如此经典之美的数学题,就会激发学生对解法作深入研究的动力.
3 解法探究
3.1 第1)小题剖析
视角1函数角度.
从证明的目标“当x≥0时,f(x)≥1”成立入手,将目标直译为在条件“x≥0”下,不等式“f(x)min≥1”成立即可.
解法1若a=1,则函数f(x)=ex-x2,求导可得f′(x)=ex-2x,此时不好判断该导数f′(x)的正负,故设g(x)=ex-2x,则
g′(x)=ex-2,
令g′(x)=0,解得x=ln 2,列表1.

表1 导函数对应值
从表1可知g(x)≥g(ln 2)=2-2ln 2>0,从而f′(x)>0,因此函数f(x)在区间[0,+∞)上单调递增,故f(x)>f(0)=1.
视角2等价转化角度.
对所要证明的不等式,如果直接不好证明,可以先进行等价变形,然后再证明其成立即可.
解法2当a=1时,不等式f(x)≥1等价变形为(x2+1)e-x-1≤0.设函数g(x)=(x2+1)e-x-1,求导可得
g′(x)=-(x2-2x+1)e-x=-(x-1)2e-x.
当x≠1时,g′(x)<0,函数g(x)在区间(0,+∞)上单调递减.而g(0)=0,故当x≥0时,g(x)≤0,即f(x)≥1.
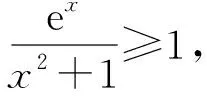
易知在[0,+∞)上g′(x)≥0恒成立,因此g(x)在x=0处取到最小值,即g(x)≥g(0)=1,故不等式f(x)≥1成立.
评注本题是一道常规不等式的证明题,既考查了学生对简单问题的转化能力,又考查了数学思想.学生在考试中容易从函数角度思考,思路如果清晰,就能够很快解决问题.若对此题进行深入研究,就会发现此题中对函数f(x)直接求导,不容易确定函数的走势,需要灵活处理:等价变形为
(x2+1)e-x-1≤0,
或
或对导函数f′(x)=ex-2x二次求导才能够解决问题,有利于对导数与函数关系的深刻理解.
3.2 第2)小题剖析
本小题是零点问题,属于高考的热点问题,求解时常将零点问题转化为方程解的问题,或转化为两个新函数的图像交点问题.一旦参数参与其中,问题就会变得复杂一些.
视角1直接分离参数.

令h′(x)=0,解得x=2,列表2如下:

表2 导函数对应值


视角2直接对参数讨论.
上述视角1的直接分离参数是常用方法,但有时也可以对参数直接进行分类讨论.本题中函数f(x)的导函数f′(x)的正负无法直接判断,因此需要对导函数f′(x)进行二次求导,当x∈(0,+∞)时,对参数a进行分类讨论.
解法2对函数f(x)=ex-ax2(其中x>0)求导可得f′(x)=ex-2ax,设g(x)=ex-2ax,对函数g(x)求导可得g′(x)=ex-2a.
由于x∈(0,+∞),下面对参数a进行分类讨论:

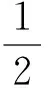
此时需要讨论1-ln 2a的正负:


联立

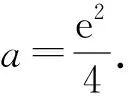

视角3直线与曲线相切.

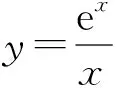
从而


视角4两条曲线相切.
借助常见的函数y=ex和y=ax2(其中a>1)的图像与性质,将“方程ex-ax2=0只有一个根”,变形为“方程ex=ax2只有一个根”,等价转化为“函数y=ex的图像和函数y=ax2(其中a>1)的图像相切”,从而求得a的值.
解法4f(x)=ex-ax2=0变形得ax2=ex.设函数g(x)=ex,h(x)=ax2,易知g(x)在(0,+∞)上单调递增.
由第1)小题ex>x2可知,参数a一定满足a>1.又函数y=ax2(其中a>1)在(0,+∞)上单调递增.结合题意“方程ex-ax2=0只有一个根”,即“方程ex=ax2只有一个根”,下面讨论的对象是指数函数y=ex与二次函数y=ax2的交点问题.
结合题设条件,易知“函数y=ex的图像”和“函数y=ax2(其中a>1)的图像”具有上升的特征,两条曲线只有相切时才能够符合题意.也就是两个函数的图像只有一个公共切点(有一条共同的切线),不妨设该切点M的坐标为(m,em).易知第一个关系式
em=am2(其中a>1,m>0),
两条曲线在公共点M处的斜率相等,可得第二个关系式
em=2am(其中a>1,m>0).

评注两条曲线相切的研究形式多样,曲线的走势多变,研究其相切的难度比较大.
视角5先等价转化,再分类.
本题中的“f(x)在(0,+∞)上只有一个零点”等价于“函数h(x)=1-ax2e-x在(0,+∞)上只有一个零点”,再讨论函数h(x)的单调性,结合h(x)的最小值分类讨论得到a的值.
解法5设函数h(x)=1-ax2e-x,则f(x)在(0,+∞)上只有一个零点当且仅当h(x)在(0,+∞)上只有一个零点.
1)当a≤0时,h(x)>0,h(x)没有零点.
2)当a>0时,h′(x)=ax(x-2)e-x.
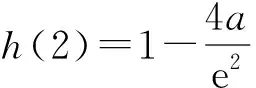

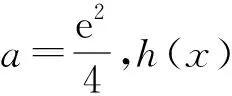

故h(x)在(2,4a)上有一个零点,因此h(x)在(0,+∞)上有两个零点.
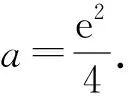
评注对参数a分类讨论,需要判断各种情况下得到的参数a的范围是否符合题意,把各种符合题意的范围取并集,即为参数a的取值范围.但有一些不等式恒成立问题需要对自变量x进行分类讨论,对各种情况下的a的取值范围取交集,即为参数a的取值范围.
4 解后反思
4.1 审题立足数学概念,思悟规律回归教材
函数零点(或方程根的个数)问题是近几年高考的热点.在函数的定义域内,探究函数单调性和极值,需要弄清函数的走势,以及函数的零点个数或零点近似值范围.本题第2)小题涉及“函数只有一个零点”,强调了“零点”的个数和唯一性等特征下,“确定”对应的参数a的值.
第2)小题解法剖析中的几种思维视角,不外乎分离参数、分离函数和等价转化等三大审题、解题策略.本题的分离参数只有视角1,分离函数有视角3和视角4,等价转化有视角2和视角5,不论哪一种策略,都会立足数学中的函数、导数等概念,如视角2中,对导函数又采用了二次求导,此时一定要切记“导函数正负决定了原函数的增减”这一根本点,在此基础上讨论极值问题或最值问题就会显得自然和舒坦.
4.2 挖掘审题视角,深究通性通法
高度重视导数、函数之间的关系(解析式、图像等),掌握函数走势(单调性、周期性、对称性等)的确定方法与技巧,既可以提高解题效率,又可以提升学生审题的自信心.近几年数学高考常常以函数为载体,在导数、方程、不等式等知识点的交汇处命制压轴题,要求学生要重视运算能力和运算速度的提高,特别是涉及参数取值范围的确定,平时训练一定要注重算理、算法和正确地分类,否则转化方式方法中的逻辑性就会混乱,简捷的思维就难以形成.

4.3 注重数学思想方法,积淀解题经验
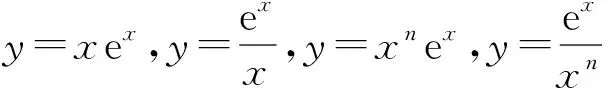
总之,还要掌握一些典型函数问题的解题策略:判断函数的单调性、求函数的极值(或最值)、证明不等式、讨论函数的零点或函数的图像等审题、解题常用的方法技巧,力争做到讨论不遗漏、分析要全面、计算要精准、思路要简捷,从而提高借用数学思想方法确定最优解题方法的选择能力,缩短解题长度和提升解题能力,有利于学生思维层次的提升,同时也积淀了多方位、多视角探究解题的经验,更加有利于学生数学核心素养的养成与提升.

