对一个二元最值问题的探究*

●

(内江师范学院数学与信息科学学院,四川 内江 641100)

《现代汉语大词典》对“探究”的解释是探索研究，即努力找出答案、解决问题．数学探究活动是围绕某个具体的数学问题，开展自主探究、合作研究并最终解决问题的过程.具体表现为：发现和提出有意义的数学问题，猜测合理的数学结论，提出解决问题的思路和方案，通过自主探索、合作研究论证数学结论.《普通高中数学课程标准(2017年)》(下文简称《标准》)指出：数学探究活动是运用数学知识解决数学问题的一类综合实践活动，也是高中阶段数学课程的重要内容[1].可见，数学探究是重要的学习方式.从学习方式的实践来看，数学探究活动一般要经历4个阶段：提出问题、分析问题、解决问题、推广问题.本文以一个二元最值问题为例，展示数学探究活动的4个阶段.

1 提出问题——探究的核心

《标准》指出：数学探究课题的选择是完成探究学习的关键.课题的选择要有助于学生对数学的理解，有助于学生体验数学研究的过程，有助于学生形成发现、探究问题的意识，有助于鼓励学生发挥自己的想像力和创造性[1].可见，好的数学问题是开展探究活动的核心.什么样的数学问题算得上一个好的数学探究问题呢？根据探究的内涵——“努力找出答案、解决问题”来看，探究必然是一个深刻的思维过程.因此，我们认为探究的问题应具备三度：一定的难度、一定的深度和一定广度.一定的难度是开展数学探究的必要，一定的深度是深入探究的前提，一定的广度是高效探究的保障.

问题已知a2+ab+b2=3，求a2-ab+b2的最大值和最小值.

问题评价上述问题具有一定的难度、深度和广度，亮点纷呈：形式优美、构思巧妙、叙述简洁、通俗易懂、不偏不怪、解法多样、内涵丰富、数学味浓、不设陷阱、可一般化.完全包含了数学家匈菲尔德在1994年提出一道好的数学题应具备5个要求：容易接受的、一题多解、蕴含了重要的数学思想、不故意设陷阱、可推广和一般化.因此，本文呈现的问题有助于学生体验数学研究的过程，有助于学生对数学的理解，是数学探究的好问题.

2 分析问题——探究的关键

分析问题指弄清问题已知条件(起点)、待求或待证目标(目标)、已知条件的等价条件、待求或待证目标的等价目标以及起点和目标之间的差异、实现目标的路径.具体来讲，探究者应清楚：已知条件是什么？已知数据有哪些？哪些条件处于支配地位、是解题的核心要素？哪些条件预示着解题的方向？由已知条件能推出哪些结论？已知条件的等价条件有哪些？待求或待证量是什么？待求或待证量的等价形式是什么？等等.分析问题是解决问题的前提，是数学探究的关键.波利亚指出：“对你所不理解的问题做出答复是愚蠢的.”[2]分析问题一般要经历两个过程：直观感知和信息加工.直观感知指对信息源提供信息的初步接受，即弄清字面意义；信息加工指对初步接受的信息进行识别、筛选、处理，包括弄懂数学含义、识别题目模式、揭示解题方向[3].

2.1 初步审题，直观感知

已知条件a2+ab+b2=3.

待求目标求a2-ab+b2的最大值和最小值.

初次审题后的感受：问题简单，但无从下手.

2.2 再次审题，信息处理

解题经验提取根据待求目标的特点，可断言：取最小值时a,b同号；取最大值时a,b异号(这正是目标取得最大、最小值对应的条件).

模式识别1配对偶式法.

记M=a2-ab+b2，则

(1)

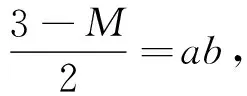
(2)

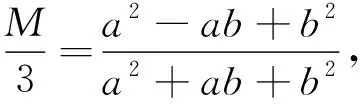
(3)

尝试1求a2-ab+b2的最值，可以转化为求式(1)或式(2)或式(3)的最值.

初中视角将式(1)和式(2)孤立来看，最值不易求得.但将两者视为整体可以发现a2+b2与ab有天然的联系：

a2+b2+2ab=(a+b)2≥0⟹a2+b2≥-2ab;

a2+b2-2ab=(a-b)2≥0⟹a2+b2≥2ab.

由上述两个不等式可以建立关于M的不等式，进而求得M的最值.

高中视角式(3)可视为求二元函数的值域问题.

二元函数的值域常转化为一元函数的值域：

模式识别2线性规划.

尝试2a2+ab+b2=3看成“约束条件”，a2-ab+b2看成是“目标函数”，作出曲线，运用线性规划知识处理，但较难.

尝试3a2+ab+b2=3看成是二次曲线，a2-ab+b2看成是“目标函数”，可运用三角换元法将目标函数转化为一元函数值域问题.但二元曲线非圆、椭圆、双曲线等常见图形，因此在三角换元时需要作一些处理：由a2+b2+ab=3，得

再运用三角换元即可.

3 解决问题——探究的重点

数学问题是数学研究的对象，而解决问题不仅是数学研究要达成的目标，同时也是数学活动的基本形式和主要内容.数学家哈尔莫斯指出：“数学家存在的主要理由是解问题，数学的真正组成部分是问题和解.”波利亚指出：“中学数学的首要任务就是加强解题训练，掌握数学就意味着善于解一些要求独立思考、思路合理、见解独到和有发明创造的题.”在数学探究中，解决问题是分析问题环节的具体实施、是数学探究的最基本形式和主要内容.探究者应力求从不同视角解决问题，通过一个问题的探究实现一小类问题的解决，通过一小类问题的解决实现一大类问题的解决，最终通过有限道题的探究去领悟解决无限道题的数学机智.

3.1 思维层次1：初中办法

解法1令M=a2+b2-ab，则

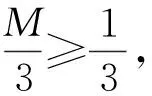
得M≤9，当且仅当a=-b时等号成立.故1≤M≤9.

解法2记M=a2+b2-ab,由3=a2+b2+ab,得

3-M=2ab，

从而

即

M≥1.

又由(a+b)2-3ab=M和(a+b)2-ab=3,得

2(a+b)2=9-M≥0，

从而M≤9,故1≤M≤9.

解法3令M=a2+b2-ab，由a2+b2+ab=3，得

a2+b2=3-ab.

因为-(a2+b2)≤2ab≤a2+b2，所以

ab-3≤2ab≤3-ab，

从而

-3≤ab≤1，

于是M=a2+b2-ab=3-ab-ab=3-2ab，

即

1≤M≤9.

3.2 思维层次2：高中办法

解法4判别式法.

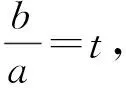
(M-3)t2+(M+3)t+M-3=0，

得

Δ=(M+3)2-4(M-3)2≥0,

于是

1≤M≤9.

解法5三角变换法.

由a2+b2+ab=3，得

于是

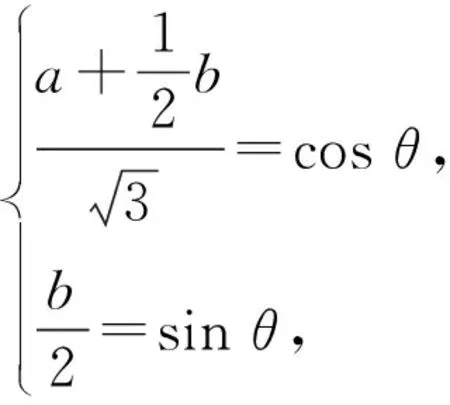
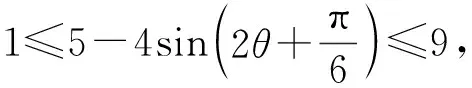
张奠宙先生指出：“在日常的中学数学教学中，能够用高等数学的思想、观点、方法去解释和理解中学数学问题的例子很多．重要的是，作为一名数学教师应该具有这样的思维意识.”我们不禁要问：能从高等数学的角度对解决方法进行解释吗？能用高等数学知识直接解决探究问题吗？

3.3 思维层次3：大学办法

模式识别3二次曲线的变换法.

a2+ab+b2=3看成二次曲线的最大的麻烦是含有ab.否则，a2+ab+b2=3即为圆的标准方程.怎样将二次曲线中交叉项ab去掉呢？下面从高等数学视角给出分析：

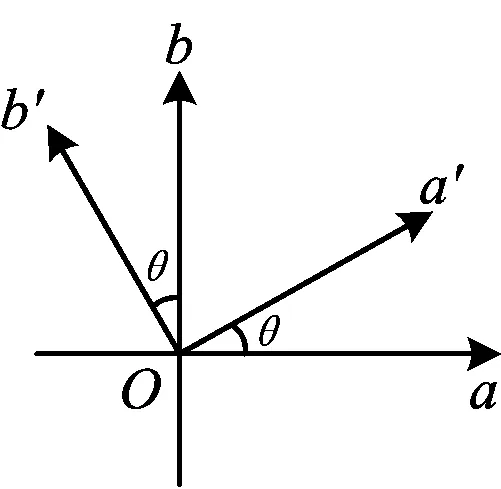
图1

解法6坐标变换法[4].

如图1，得

a=cosθ·a′-sinθ·b′,

b=sinθ·a′+cosθ·b′，

代入a2+ab+b2=3中，可得

(1+cosθsinθ)a′2+(1-cosθsinθ)b′2+(cos2θ-sin2θ)a′b′=3.

(4)

令cos2θ-sin2θ=0，得

cosθ=sinθ,

即

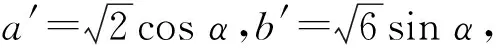
a2+b2-ab=(1-cosθsinθ)a′2+

(1+cosθsinθ)b′2+(sin2θ-cos2θ)a′b′=

1+8sin2α,

从而

1≤1+8sin2α≤9，

得a2+b2-ab的最大值为9，最小值为1.

解法7正交变换法[5].

令z=a2+b2+ab-3，则

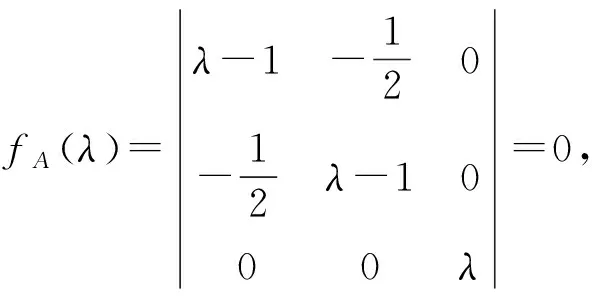
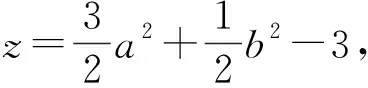
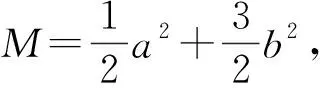
模式识别4拉格朗日乘数法[6].

在高等数学中，解答多元函数最值问题的最直接方法是拉格朗日乘数法.

解法8拉格朗日乘数法.

令M=a2+b2-ab，l(a,b,λ)=a2+b2-ab-λ(a2+b2+ab-3)，再令la=2a-b-λ(2a+b)=0，lb=2b-a-λ(2b+a)=0,lλ=-(a2+b2+ab-3)=0,则

得a=±b.当a=b时，a2=1，则Mmin=a2=1；当a=-b时，a2=3，则Mmax=3a2=9,故a2+b2-ab的最大值为9，最小值为1.

4 推广问题——探究的难点

数学推广是指在一定范围内或一定层次上对数学概念、定理、法则进行拓展，使之在更大范围或更高层次上成立.此外，也指对条件、结论进行结构分析以后，进行适当变化，使得到的新命题为真[7]．张景中院士指出：“推广是数学研究中极其重要的手段之一，数学自身的发展在很大程度上依赖于推广.数学家总是在已有知识的基础上，向未知的领域扩展，从实际的概念及问题推广出各式各样的新概念、新问题.”[8]

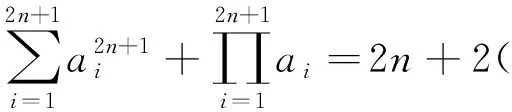
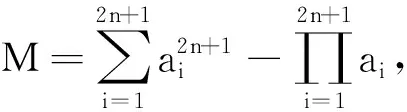
从而M≥2n，当a1=a2=…=a2n+1时，等号成立.

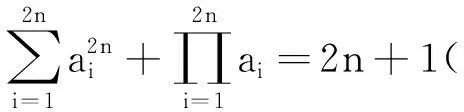
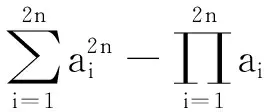
于是

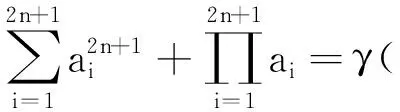
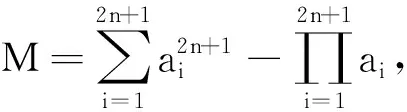
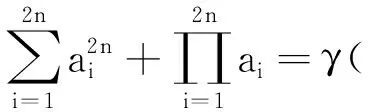
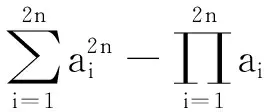
于是

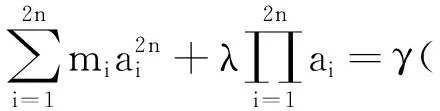
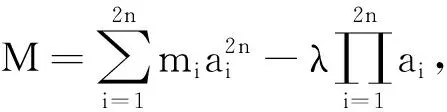
从而

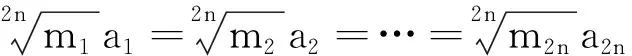
波利亚指出：一个有责任心的教师与其穷于应付烦琐的数学内容和过量的题目，还不如适当地选择某些有意义但又不太复杂的题目去帮助学生发掘题目的各个方面，在指导学生解题的过程中，提高他们的才智与推理能力.本文的数学探究正是通过对一个好的问题从不同层面反复、深入地剖析，实现学生能力提升、认知结构优化和解题经验的积累.因此，数学探究无可厚非地成为了当前最为重要的学习方式.