品读平面向量考题 构建复习教学框架*

●

(温州第二高级中学，浙江 温州 325000)

平面向量是高考的重要考点之一，是架起平面几何图形与坐标系下代数运算的知识枢纽．综观2018年全国各地数学高考卷的平面向量试题，有对向量基本运算的考查，也有创新背景探寻数形转化的思想，凸显向量的学习与应用意义．

1 基于双基考查的考题品读

平面向量的线性运算、基本定理及坐标表示是向量的基础知识，也是高考重点考查的内容．在应用的过程中，平面向量融数、形于一体，具有代数形式与几何形式的双重身份，构成了向量解题中的两种基本方法．

例1设a,b均为单位向量，则“|a-3b|=|3a+b|”是“a⊥b”的

( )

A.充分而不必要条件

B.必要而不充分条件

C.充分必要条件

D.既不充分也不必要条件

(2018年北京市数学高考理科试题第6题)

分析本题考查向量模的计算与垂直关系的判断，将|a-3b|=|3a+b|两边平方，得

a2+9b2-6a·b=b2+9a2+6a·b，

则

a·b=0，

即

a⊥b.

故选C．

也可以设a=(cosα,sinα)，b=(cosβ,sinβ)，通过坐标运算得到

cos(α-β)=0，

推得a⊥b．

( )

(2018年全国数学高考卷Ⅰ理科试题第6题)

分析本题考查平面向量的线性运算与基本定理,即

线性运算转换的方法有很多，可以利用中线关系

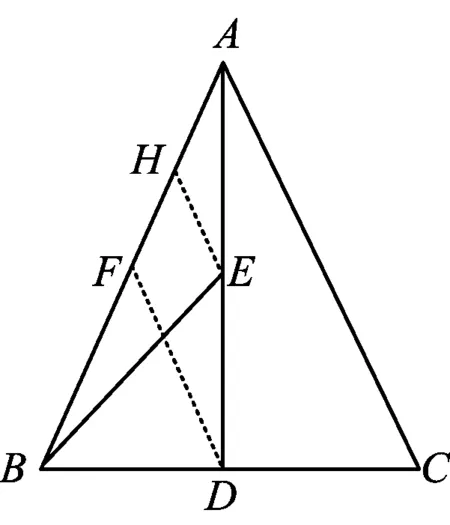
图1

线性运算是以基底向量为目标的分解与合成运算，借助平行四边形法则与三角形法则完成，可添加辅助线.如图1，先取

AB的中点F，联结DF，再取AF的中点H，联结HE,可得

2 基于几何背景的考题品读

向量表示与运算中涵盖着有关长度、角度和垂直关系的问题，在解题中探寻出这些几何要素，借助图形的关系，可以大大简化运算的难度．

( )

(2018年浙江省数学高考试题第9题)

分析本题的难点是b2-4e·b+3=0，化简得

(b-e)·(b-3e)=0，

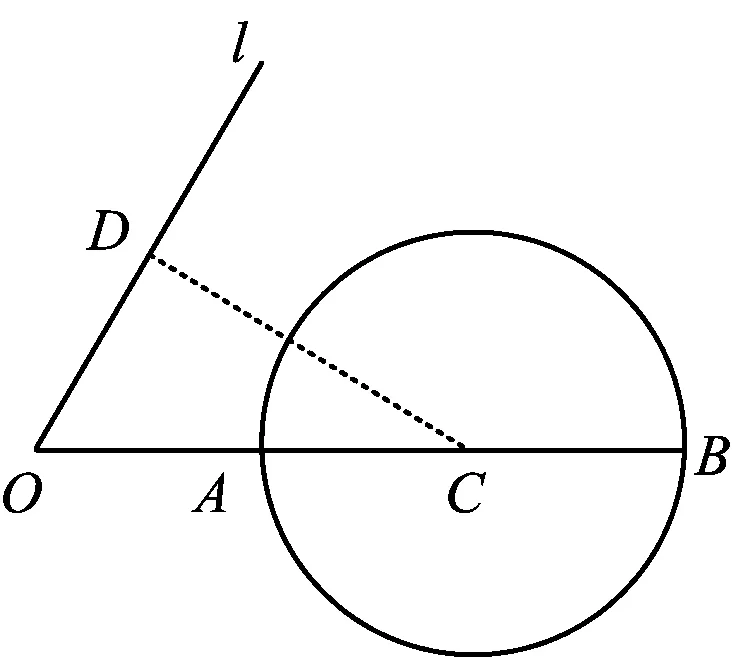
图2

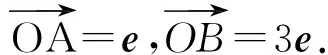
对向量关系(c-a)·(c-b)=0，可推广为

(c-a)·(c-b)=λ(其中λ≠0)，

通过极化恒等式的可化简为

(c-a)·(c-b)=

则

( )

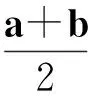
(2018年天津市数学高考理科试题第8题)

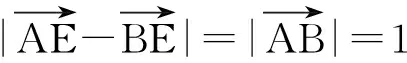
图3 图4

如图3，取AB的中点F，得

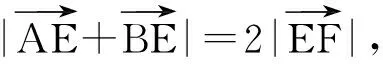
3 基于构造向量的考题品读

以平面向量为载体，结合其他知识的考查是高考命题的一个亮点，常常与解三角形、解析几何、三角函数等内容交叉渗透，既能对图形的性质与特征赋予代数的运算，又能将抽象的代数巧妙地转化为几何关系，使得解题处处妙笔生花．

例5在△ABC中,角A,B,C所对的边分别为a，b，c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为______.

(2018年江苏省数学高考试题第13题)

分析因为点A,C,D共线，结合角平分线定理，得

两边平方得

化简得

a+c=ac,

即

运用柯西不等式，得

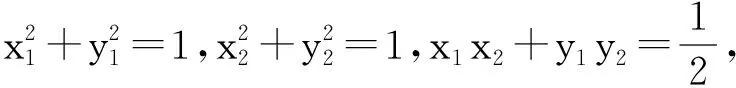
(2018年上海市数学高考试题第12题)

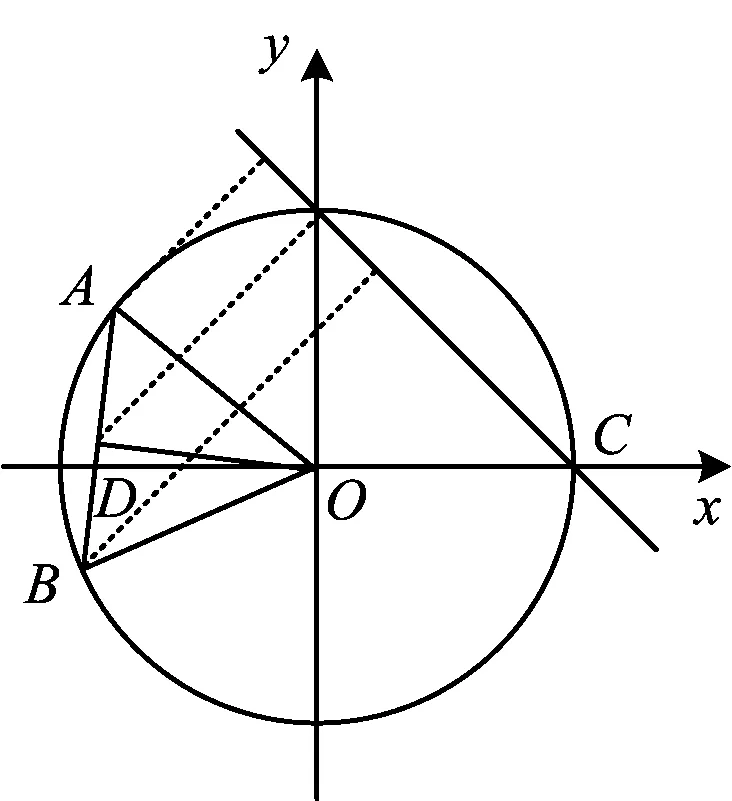
图5

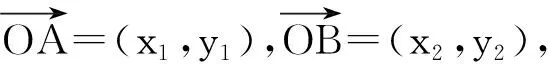
得△ABO是正三角形．设C(1,0)，且AB的中点为D，取直线l:x+y-1=0的垂直向量为m=(1,1)，从而

4 构建平面向量的复习教学框架

“高考考什么与怎么考”如同一面镜子，照出“教师教什么以及怎么教”．解读高考试题的特征与思路，反思教学行为，回归课堂，尤其是高三的复习课，从数形思想、几何背景与运算工具这3个角度去主动构建起复习教学的框架，更好地对经典数学问题进行回溯，让复习教学更加有效．

4.1 明确平面向量代数与几何双角色，凸显双线

在平面向量的知识点复习过程中，例题的示范应凸显双线，双管其下，让学生感受到手中有两招，可选择可优化，形成几何与代数这两个解题流程．明确双线的定位，教师在教学中能更好地有的放矢．例如，在三角形的四心向量形式的问题上，学生受困于向量形式的多变，无法下手，其原因多在于教师过于注重几何形式的推导，若能增加代数方法，将三角形特殊为直角三角形，建系算出四心坐标，就能轻松解决．双线框架的建立让学生从想不到的困境中走出来，变成此路不通另谋出路，指明了方向．

4.2 积累平面向量几何背景的转换形式，画龙点睛

平面向量解题的难点之一是对向量形式所涵盖的几何背景的转换.在复习过程中，可通过典型例题的学习提炼模型，不断积累，形成以共线、圆、垂直、极化恒等式、三角绝对值不等关系等几何背景框架．学生面对高考题，能快速有效地反馈信息，锁定模型特征，联想过往相似类型对应的解题思想与方法[1]．

沿着这一思路，学生能轻松识别圆的向量形式，即|a-b|=1是距离为定长引发的圆；(a-c)(a-b)=0由圆周角为90°联想到圆；|a|=2|a-b|是阿波罗尼斯圆．其他几何背景也是如此，归纳解题模型是成功解答高考试题的有效方法之一．

4.3 注重平面向量运算工具的灵活使用，纵横交汇

平面向量是一个运算的工具，具备形与数转化的便利，学习过程中应该不断地尝试并发散联想：一方面在有显著几何特征的图形中寻找向量关系，比如在△ABC中，在边BC的中线AD背景下，就容易联想到

平方再相加得到

得到关于中线的一个等量关系，由极化恒等式得到

另一方面在代数运算的情景下构造向量关系，比如对2018年浙江省数学高考试题第11题中出现的方程组

当z=81时，得

从而求解过程就可以理解为

(19,73)=x·(1,5)+y·(1,3)，

这是一个向量的线性运算．