一道浙江省数学竞赛题的“源”与“流”*
●
(杭州学军中学,浙江 杭州 310012)
2018年浙江省高中数学竞赛颁奖大会已经结束,笔者有幸参加了此次会议,并在会议上做了一个20分钟的讲座,内容是对一道省赛题的思考.会后笔者与一些专家和同行进行了交流,讲座的内容反应良好,故笔者将其整理成文,和读者分享.
题目将2n(其中n≥2)个不同整数分为2组:a1,a2,…,an;b1,b2,…,bn,证明:
(2018年浙江省高中数学竞赛试题第14题)
1 源头和背景
本题是一个改编题,经过搜索,笔者找到了该题的源头.
源题证明:对于2n(其中n≥2)个不同实数a1,a2,…,an;b1,b2,…,bn,有
(1999年波兰数学奥林匹克试题第二天第2题)
该题的2n个数是实数,而浙江省赛题是2n个整数,整数与实数的本质区别在于整数具有离散性,即任意两个不同整数之差的绝对值不小于1,也正因为如此,省赛题中不等式右边的代数式才会有一个正的下界.
会后,笔者和命题组教师进行了交流,得知该竞赛题的背景来源于高等数学中的矩阵[1].不妨设a1 其中矩阵LT为矩阵L的转置,于是 |ai-bj|+|aj-bi|-aj+ai-bj+bi=(|ai-bj|+ai-bj)+(|aj-bi|+bi-aj)≥0, 故对任意i,j∈{1,2,…,n},有 |ai-bj|+|aj-bi|≥|ai-aj|+|bi-bj|. (1) 由式(1)可知,Tn≥‖S‖≥n. 由此可知,源题的结论也成立.此证明过程简洁明了,但因背景涉及到高等数学,故命题组给出了一个较为复杂的初等证明方法. 1)当n=2时,不妨设a1 T2=|b2-a1|+|b2-a2|+|b1-a1|+|b1-a2|-|a2-a1|-|b2-b1|. ①当a1 ②当a1>b1时,T2=b2-a2+a1-b1+|b1-a2|+b1-a2≥2. 2)假设当n时命题成立,即有Tn≥n;当n+1时,不妨设a1 (2) ①若存在k,使得bk 即式(2)成立. ②类似可证,当an+1 综上所述,式(2)成立,故Tn+1>n+1,即原不等式得证. 评注由于原问题是一个与正整数n有关的命题,故考虑用数学归纳法.证明过程条理清晰,但归纳过渡部分的分类讨论难度较高,给人以入手容易走出难之感.笔者从问题的代数特征出发,以关注整体、追求简易为目标作了探究,发现了一种较为简洁的证明方法. 证法2不妨设a1 经过思考,得到如下结论: 结论1下界n是最优的. 结论2Tn不存在有限的上界. 证明1)由证法2可知,当a1 既然不存在有限的上界,那么能否找到一个可变的上界呢?也就是说能否找到一个关于n的表达式来做Tn的上界呢?经过探究得到结论: 证明考虑调整法[2].不妨设a1 (3) 考虑到a1 将上面4个式子代入式(3)可知 S*-S=4(p-q)(xt+1-xt)>0. 因此,若存在相邻的两项bp,aq满足p>q,ap>bq,则将ap,bq交换位置,可使得Tn增大.如此不断调整,直至对于任意的p>q,均有ap a1 又因为ai≥b+i-1,bi≤a-n+i,所以 对于原不等式,笔者还考虑了如下的结论: 证明不妨设对于任意i∈(1,2,…,n),均有ai,1 下面考虑上式右边的最小值: 对于任意s∈{1,2,…,n},将a1,s,a2,s,…,ak,s由小到大排序为b1,s 当bi,s=b1,s+i-1(其中i=1,2,…,k,s=1,2,…,n)时,取到等号. 作为教师,在平时解题的过程中,当有探究、扩展意识,而对问题的探究和扩展应建立在对题目有着精确剖析的基础上.在剖析题目时,确立合适的目标是最为重要的因素之一.确定了恰当的目标,不仅可以使得解题的过程更加自然,而且还能够对问题从多角度展开探索,通过比较和鉴别,选出理想的方法,是实现简单自然解题的关键,也是探究数学奥秘的重要素质.
2 解法





3 探究




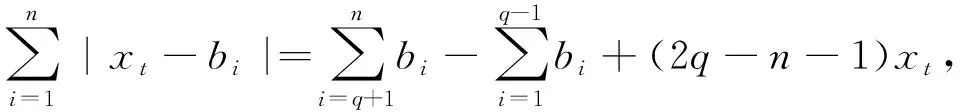
4 推广


5 感想

