2018年浙江省数学高考第9题多维赏析*

●

(吴兴高级中学,浙江 湖州 313000)

●沈新权

(嘉兴市第一中学,浙江 嘉兴 314000)

2018年高考已落下帷幕，浙江因高考招生制度改革，数学试卷显得格外引人注目，其中的第9题秉承了浙江卷简洁、朴实、灵动的一贯风格，试题既考查了学生对向量的基本概念(如向量的夹角、数量积和模等概念)的理解，又进一步考查了学生的方程、数形结合、转化化归等数学思想，是一道具有较好区分度的好题．本文通过对第9题的多视角思考和多维赏析，意图揭示命题的立意和本质，给教学带来有益的启示．

1 原题再现

( )

(2018年浙江省数学高考试题第9题)

2 解法赏析

2.1 坐标法

坐标法是解决向量问题的重要方法之一，其特点就是用代数的方法处理几何问题，思维起点低，易于操作.

解法1设e=(1,0)，b=(x,y)，因为b2-4eb+3=0，所以

x2+y2-4(1,0)(x,y)+3=0，

即

x2+y2-4x+3=0，

亦即

(x-2)2+y2=1.

点评解法1直接利用向量的坐标运算快速求解，思维量小，运算量也不大，但在坐标系的选择上要合理，否则会人为增加运算量.

2.2 几何法

向量具有代数形式和几何形式的双重身份，因此在处理向量问题时往往可以从代数的视角去审视和分析，利用数形结合的思想，见数思形，以形助数，确定解题的策略.

2.2.1 方程思想，简化条件

利用方程思想对条件进行分析、化简，探寻向量的几何意义，从而寻求解题路径.

解法2通过解方程，寻求向量b的轨迹.因为b2-4eb+3=0，则

(b-2e)2-4e2+3=0，

所以

(b-2e)2=1，

即

|b-2e|=1.

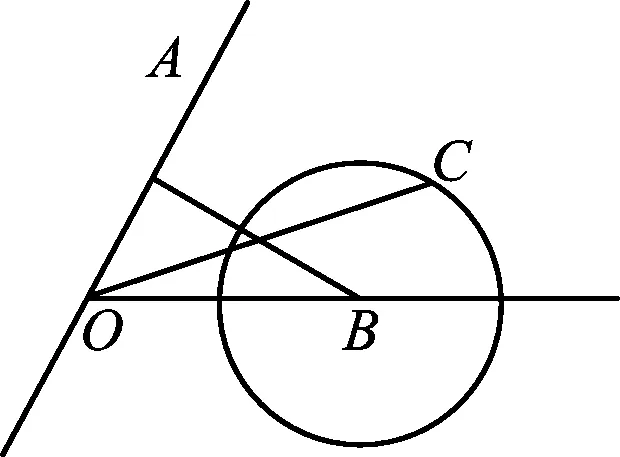
图1

点评题干涉及到向量的模、向量数量积的运算，但考虑到向量b所满足的条件是一个一元二次方程，考生对此十分的熟悉，因此解法2利用方程的思想进行求解，自然顺畅，具有一定的普适性.

解法3通过因式分解，寻求向量b的轨迹.因为b2-4eb+3=b2-4eb+3e2=0，所以

图2

2.2.2 由“形”而思，合理构造

问题的“形”往往蕴含着解题的思路与方法.本题是向量模的最值问题，不妨从模不等式入手，进行合理构造，寻求解题思路.

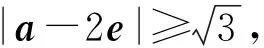
|a-b|= |(a-2e)-(b-2e)|≥

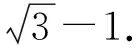
点评解法4基于|a-b|，由向量a,b的模的特征构造三角不等式，充分利用了模不等式，思维起点低，解法快捷、灵动，其中a,b几何意义的确定是关键.

2.3 向量法

2.3.1 活用极化恒等式

本题的核心是对数量积eb的处理.数量积的运算主要有3条路径，即定义法、投影法和公式法.极化恒等式将几何与代数有机结合，巧妙转化，是解决向量问题的重要工具.

解法5因为b2-4eb+3=0，所以

b(b-4e)=-3.

由数量积极化恒等式的代数形式得

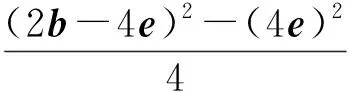
即|b-2e|=1，下同解法2.

解法6由解法5得

图3

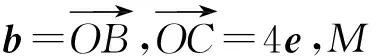
b(b-4e)=BM2-MC2=

BM2-4=-3,

即

BM2=1，

从而|b-2e|=1，下同解法2.

点评本解法通过极化恒等式，巧妙地将数量积进行转化，快速得到向量b的轨迹，从而找到解决问题的突破口.

2.3.2 活用数量积定义

定义是数学之本，是定理、性质之源.因此，在研究数学问题时，利用定义是一条路径，虽然有时会导致解题繁杂，但意义重大.

解法7设向量b与单位向量e的夹角为θ，则

b=(|b|cosθ,|b|sinθ).

因为

b2-4eb+3=0，

所以

b2+3=4eb=4|b|cosθ，

即

从而

设x=b2+3，且

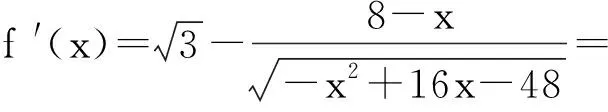
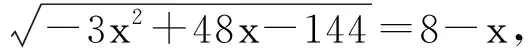
因为b2+3=4eb=4|b|cosθ≤4|b|，所以

b2-4|b|+3≤0，

即

1≤|b|≤3，

从而

x=b2+3∈[4,12]，

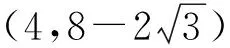
即

点评本解法虽然不漂亮，也很繁，但从培养学生的思维能力、运算能力看，解法7价值不菲，从数量积的定义到函数的构造，环环相扣，都是对学生思维力和意志力的考验.

3 拓展引申

综合上面的多维赏析可以看到，解决本题的焦点就是对|a-b|的理解．

从向量的角度来看，|a-b|就是两个起点相同的向量a,b所对应的终点的距离．解法2和解法3就是在此基础上找到了问题的突破口．

借助坐标系，从代数的角度来看，|a-b|实际上就是两个n维向量a=(x1,x2,…,xn)与b=(y1,y2,…,yn)所对应的两点间的欧氏距离(这个问题中的向量是二维向量)：

解法1实际上就是对解法2和解法3这两种几何解法的代数解释．

《普通高中课程标准(2017年)》(以下简称《课程标准》)所强调的数学核心素养之一就是数学建模，因此，通过上面的赏析和拓展，可以让学生感受到|a-b|这个距离模型在解决向量问题中的作用，从而体会数学模型的简洁性，并且能够更好地理解数学本质．

4 感悟与反思

4.1 关注数学试题的研究和教学价值

解题教学在高中数学教学中有着重要的地位，而高考试题则是解题教学中不可多得的习题来源.在教学中，不仅要提倡一题多解，将数学知识与方法串联起来，形成知识体系；更要关注试题背后所蕴含的数学本质，通过教师的研究，引导学生去领略、去感悟试题的数学价值，借此培养学生的发散思维，提升学生的数学核心素养.

2018年浙江省数学高考卷为高中数学研究和教学提供了很好的蓝本，不少题目都具有很强的导向性，其中的第9题就是一个很好的例证，试题亲和、简约而不简单，朴实无华，但内涵极其丰富，蕴含着极高的研究价值，是解题教学的极好素材.

那么如何研究高考试题？又如何让高考试题发挥其应有的教学价值呢？

数学是思维的体操，数学教育很重要的一个方面就是培养学生的思维能力，因此，一个数学问题的每种解题方法都意味着不同的思维方式，都有其独特的思维价值和教学价值．

4.2 重视数学试题的解法研究

向量整合了大小与方向两个维度，是数形结合的天然工具，是沟通代数、几何、三角的桥梁，是连接初等数学与高等数学的纽带，具有重要的应用价值和人文价值．新课程改革以后，向量从幕后走到了台前，成为高中数学的核心概念之一，运用向量法解题也得到了空前重视．

解决向量问题的坐标法思维起点低，是通性通法.对于易于建系的向量问题采用坐标法有利于问题的解决，但对学生的数学运算有较高的要求．坐标法解向量题，用计算代替演绎，体现了机械化思想，在某些方面与几何法和向量法相比更有优势．几何法的特点是数形结合，由数及形可以直达问题的核心，简化问题的解决，这需要学生有较好的数学直观想象能力，这种方法可以使得问题的解决“算得少一点”．向量法是在深刻理解向量的概念和运算的基础上解决向量问题的方法，向量法既有几何法的灵巧，又有坐标法的方便，也能够更好地揭示平面向量问题的本质.

4.3 加强数学试题不同解法之间的比较

坐标法、几何法、向量法解决向量问题，蕴含着丰富的数学思想方法，这些思想方法并非一定会给解题带来立竿见影的作用，但是如果有思想方法的指引，我们的解题教学会站得更高、看得更远，使得解题更有品味，使得学生更能够体验到数学解题带来的愉悦．

向量中的坐标法体现算法思想和机械化思想，几何方法则有利于培养学生的数学直观想象能力.向量法运用得好，不仅可以培养学生的逻辑推理能力，甚至还可以启发学生利用几何法解决向量问题的解题思路，因此，向量法与几何法之间并没有难以逾越的鸿沟，从知识联系的角度来讲，这两种方法是一脉相承的.

因此，在教学中，教师应引导学生理解不同的解题方法都有其相应的应用范围，没有一种解题方法能够包打天下．就拿处理向量问题来说，坐标法思路简单但计算复杂；几何法虽然计算简单，可以直达答案，但思路巧妙；向量法要求学生对向量概念和运算的理解入木三分．因此，在教学中，我们要让学生理解不同的解题方法之间都各有利弊，尽量避免非此即彼的观点，教学中要引导学生去比较、鉴别不同方法之间的优劣，不能单纯以方法的繁简作为取舍的唯一尺度，更不能为了提高解题速度而过分追求所谓的解题技巧．否则，解题教学就会陷入“一题一法”的怪圈，淹没在无边无际的题海中，这与《课程标准》所倡导的培养学生的数学核心素养是相背道而驰的．