高中数学多元化概念教学的实践和教学反馈策略的探讨
梁必文
[摘 要] 数学概念是数学知识的重要基础,要想使学生学好数学,培养学生的数学思维,必须使学生牢固掌握数学概念,这也是学生学好数学的关键. 本文通过介绍实施高中数学概念教学的多元化案例,以及实施相应概念教学后的效果反馈,探讨如何在新课改下改革高中数学概念教学,提高課堂教学的效果.
[关键词] 高中数学;概念教学;教学反馈
前言
苏联知名数学教育家A·A斯托里亚尔在《数学教育学》这本书中提到:“数学教学是激发学生数学思维的活动,它并不仅仅是数学活动的结果,即不仅仅是将数学知识灌输给学生.”数学概念是数学知识的重要基础,要想使学生学好数学,培养学生的数学思维,必须使学生牢固掌握数学概念,这关系到学生的长远发展. 在上个学期,笔者选择了两个班进行了一次实验,在实验班中使用多样化的概念教学法,用对照班的成绩显示出多元化概念教学法的功能.
高中数学概念教学的实践
1. 使用游戏法
游戏是学生喜闻乐见的活动方式,在教学“归纳推理”的概念时,笔者使用了游戏法. 具体课堂实录如下所示:
师:同学们,今天我和大家一起做一个小游戏,看看谁最聪明. 现在请两个同学上讲台来比试一下,行吗?(学生纷纷举手,笔者邀请了甲、乙两个学生)
师:在你们面前,我准备了三顶帽子,分别是2顶红帽子,1顶黄帽子. 你们先把眼睛闭起来. (笔者给甲、乙分别戴上一顶帽子,并将剩下的帽子藏起来)
师:讲台下的同学不要说话,甲同学和乙同学现在睁开眼,说说自己帽子的颜色(两位同学互看了一下,并迟疑了几十秒钟,然后同时说出:“我们戴的是红帽子. ”)
师:不错,你们都说得很对,那大家说说,甲、乙谁更聪明.
生:都聪明.
师:那大家说说甲、乙是如何知道的?
生:他们看彼此的时候都犹豫了一下,要是知道自己戴的是黄帽子,那对方就应该立马说出自己所戴的帽子的颜色.
师:你们观察得很认真,推理正确,现在请大家看一组PPT.
展示PPT课件:①天空黑云密布,蜻蜓低飞,你们想到了什么?②小草绿了,花儿开了,小树开出了新芽,你们想到了什么?
生:第一组说明要下雨了,第二组说明春天来了.
师:你们说得很对,你们结合刚才的游戏,再结合自己的生活经验,能说说什么是推理吗?
生:推理就是由一组特殊现象去推测某个结论的过程.
师:对的,所谓推理,是结合一个或几个事实来明确一个新的判断的思维过程. 从结论来说,推理就是前提加结论. 我们将从个别事实推演到一般性结论的推理称为归纳推理.
上述案例通过游戏法和生活案例,引导学生逐渐掌握了归纳推理的含义,收到了良好的教学效果.
2. 使用实验法
高中生的实验能力已经得到了初步发展,在教学新数学概念时,我们教师可以引入实验法,比如笔者在教学“任意角”的概念时,使用了实验法. 下面是课堂实录过程:
师:今天,我们先来做一个实验,考验大家的反应速度. 我手上拿着一个钟,上面显示是中午12:00,分针和时针都靠在一起. 现在我来转动分针,你们来回答钟面时间,再说说分针转过的角度. (开始慢慢转动分针,学生踊跃回答)
学生回答的结果如表1所示:
师:经过刚才的实验,同学们有什么发现?
生:觉得角的范围不止[0°,360°].
师:从12:00到13:10,分针转了多少度?
生:不止转了360°.
师:如果分针走三圈,转了多少度呢?
生:1080°.
师:对,这种转几圈然后又回到原始位置的现象,就是我们常说的“周而复始”,你们还能说说生活中有类似现象么?
生1:火车到站,再开出.
生2:一年四季轮流交替.
师:你们都说得很对. 今天,我们来学习一个周而复始的模型——三角函数. 大家先来说说你们是怎么定义角的.
生:从一个顶点出发的两条射线所组成的图形.
师:经过刚才的实验,你们认为角是不是应该重新定义?
生:是的,我觉得角应该是一条射线从一个位置旋转到另一个位置所形成的图形.
师:这位同学说得很对. 现在我们来看看PPT是怎么演示角的. (PPT演示角,使学生感受到角并不是一个静态概念,而是动态的)
师:同学们现在再看看,分针从12转到3与从12转到9,这之间有什么区别?
生:从12转到3,分针按顺时针方向转了90°;从12转到9,分针按逆时针方向转了90°.
师:那我们应该怎么区别这不同的90°呢?
生:可以用正负角来区分.
师:回答得不错. 现在我们就来下定义,按逆时针方向旋转所形成的角叫作正角,按顺时针方向旋转所形成的角叫作负角.
师:如果射线没有作任何旋转呢?
生:零角.
师:送样就把原来学的范围[0°,360°]的角推广到了任意角,包括正角、负角和零角.
在这次教学中,笔者通过实验导入,使学生直观地看到角的动态变化,帮助学生走出了思维定式,意识到角的范围不止[0°,360°],在这种情况下再引入任意角的概念,学生很容易就能接受了.
3. 使用类比法
很多知识具有相似性,这为我们实施类比法提供了契机,笔者在教学“直线的斜率”这个概念时,使用了类比法. 笔者在教学中设置了“爬山坡”的情境,抓住山坡坡度与直线斜率都属于刻画倾斜程度的量,引导学生产生类比联想,理解直线斜率的本质. 本节课的课堂实录具体如下:
师:同学们,今天我们先来学学《平面解析几何图形》中最简单的几何图形——直线. 大家对直线是不是非常熟悉啊?
生:是的!(异口同声)
师:大家说说过几点能确定一条直线?
生:过两点.
师:过一个点能做多少条直线呢?
生:无数条!
师:那这些直线有何共同点?
生:都经过同一点.
师:你们说得很对. 那这无数条直线又有什么区别?
生:它们的方向不同.
师:方向不同又能体现直线的什么特点呢?
生:说明直线的倾斜程度不一样.
师:对,在前面,我们已经学习了可以用坐标来表示点,那么直线的倾斜程度可以用什么表示呢?我们先来看一组PPT.
展示PPT:
师:假如我们现在要去登山,这两个三角形就类似两座山,你们会选择哪座山去登呢?
生1:我选第一座. 因为第一座山看起来比较平缓,比较容易爬.
生2:我想选第二座. 因为第二座山看起来比较陡峭,具有一定的挑战性.
师:两座山各有千秋. 那么山坡的平缓和陡峭用什么刻画呢?
生:坡度!(异口同声)
师:那你们怎么计算坡度?
生:用高度除以宽度就是坡度.
师:那你们看看PPT上的两座山,坡度分别是多少?
师:你们计算得都是对的. 那我们是否可以认为坡度就是山坡的倾斜程度?
生:可以!
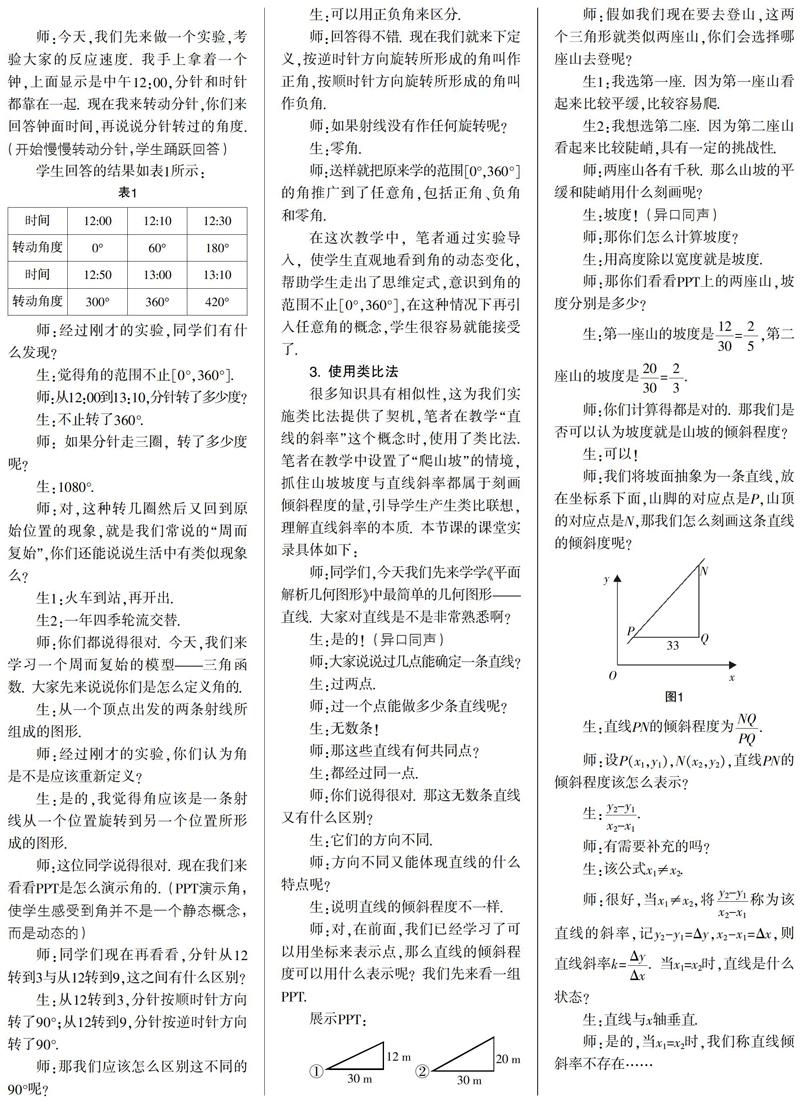
师:我们将坡面抽象为一条直线,放在坐标系下面,山脚的对应点是P,山顶的对应点是N,那我们怎么刻画这条直线的倾斜度呢?
生:直线与x轴垂直.
师:是的,当x1=x2时,我们称直线倾斜率不存在……
在上述案例中,笔者使用了类比导入法,直线的斜率与山坡的坡度有一些相似之处,笔者引导学生展开想象,通过坡度构建直线斜率的公式,这样可以将学生的新旧知识有机地结合在一起,根据已有的知识基础获得新的知识,学生在无形中也能掌握类比思想,进一步发展数学思维能力.
高中数学概念教学的反馈策略
1. 学生的成绩分析
经过一个学期的实验之后,实验班和对比班的数学成绩发生了一些变化. 表2是实施多元化概念教学法之前实验班和对比班的期末成绩比较:
通过四个月的实验,实验班和对比班的期末成绩比较如表3所示:
通过表2和表3的数据对比,不难发现多元化概念教学法的应用确实对高中生的数学学习成绩产生了一些影响,实验班学生的数学成绩有了明显提高,平均分、及格率和优秀率都有了明显进步. 反观对比班的成绩,几乎没有太大的变化,这足以说明新型教学法在提高学生数学学习成绩方面的作用.
2. 学生的访谈分析
笔者对本班的学生进行了访谈,让他们对教师使用的概念教學法进行了评价. 下面是访谈结果:
笔者:你们觉得老师使用概念教学法好不好啊?
生:好!
笔者:你们觉得游戏法、实验法有什么好处?
生1:我觉得更能调动课堂气氛,有时候我们刚接触上一节课的学习,神还没回过来又要学习新的数学知识,难免觉得跟不上,这时候如果老师用了比较新颖的教学法,能很快集中我们的注意力,让我们更快地进入到新课程中.
生2:我觉得能使数学知识变得更好学了. 现在的高中数学知识太难学了,但是老师用一些案例,可以让我们感觉到数学并不是那么难学,慢慢地就有学习数学的兴趣了.
笔者:那你们比较喜欢哪种概念教学法呢?
生1:我比较喜欢类比法,这样可以调动我们的求知欲,使我们联系已有的知识学习新课程,这样更容易理解新知识.
生2:我比较喜欢游戏法(笑),感觉更活泼一点.
根据对学生的访谈可以看出,学生对高中数学概念教学持肯定意见,这说明实验法、游戏法的合理使用确实能改善课堂教学效果,调动学生的学习兴趣,使学生更容易接受新的数学概念.
结论
教学无法,贵在得法,高中数学概念教学的方法丰富多彩,值得我们教师不断探索,为学生学好数学奠定基础.

