初中数学教学中归纳推理意识的渗透

刘桂花

(黑龙江省佳木斯市第四中学 154000)

一、归纳推理概述

归纳推理作为数学思想方法的一种，具体指的是可以根据某一类事物部分对象所具备的某种性质，推理得出该类事物所有对象都具有这种性质的一种推理方法，该推理过程简单来说即是从特殊到一般的过程，属于合情推理.举一个简单的例子，对于平面图形来说.正方形内角和为360°，长方形的内角和是360°，梯形的内角和也是360°，而正方形、长方形、梯形都是四边形，所以，平面内的一切四边形内角和都是360°.该例子从正方形、长方形、梯形的内角和分别都是360°这些同一事物部分相同的特点，推出“平面内一切四边形内角和都是360°”这样一般性结论的过程，就属于归纳推理.

二、归纳推理意识在初中数学教学中渗透的作用

有助于加深学生对于数学知识的理解.初中数学学习在逻辑思维及空间几何思维上对于学生提出了更高的要求，尤其是对于几何方面的问题需要学生具备足够的逻辑思维推理能力才能够对几何知识做到深入理解并应用.教师在数学教学过程中通过进行归纳推理意识的渗透，使得学生遇到较为复杂的几何难题时，能够通过利用一些简单的几何知识点进行归纳推理，围绕题目本身，从小处着手，化繁为简，化难为易，顺利实现几何难题的解答，正是学生对于一些基础的数学定理知识有着深入的理解，才能够见微知著，顺利实现问题的解决.

三、初中数学教学中归纳推理意识的渗透措施

1.引导学生进行自我探究式学习

在数学教学中，对于归纳推理意识的渗透需要教师结合实际教学目标利用相关案例对学生加以引导，调动学生思维，让学生主动参与到课堂教学中来，充分实现学生归纳推理意识的培养.例如在进行“平方差公式”教学过程中，教师可以进行如下教学设计，引导学生进行归纳推理探究学习.

首先在黑板上写出下列公式并要求学生认真观察并讨论：

待学生充分观察并完成讨论后教师可以让学生站起来说出自己的猜想，然后教师可以继续提问：根据自己的猜想，若已知25×25=625，那么可以快速得出24×26的答案吗？待学生根据自己的猜想来完成答案的验证之后，教师还可以鼓励学生自己来举一个相似的例子，并用具体的符号将自己总结的猜想规律表达出来，最后引导学生利用多项式来证明自己归纳总结的规律是正确的.

教师通过在“平方差公式”课堂教学中引导学生利用归纳推理方式进行自主探究式学习，可以使得学生的思维充分得到锻炼与提升，凸显出学生的课堂主体地位，并有效完成了“平方差公式”的认识任务，学生在学习平方差公式的过程中显然不是单纯的依赖老师“教”的，而是由自己自主探究“归纳”及“总结”出来的，相比于教师直白的讲述，这样更能加深学生对于“平方差公式”的理解与记忆，教师只需要在旁做好必要引导与帮助，即可顺利完成课堂教学任务，提升学生的课堂效率，通过引导学生进行自我探究式学习，将归纳推理过程与自主探究式学习完美结合，从而使得学生的归纳推理意识得到充分的培养，有效提升学生课堂学习效率.

2.选择针对性的习题进行讲解分析

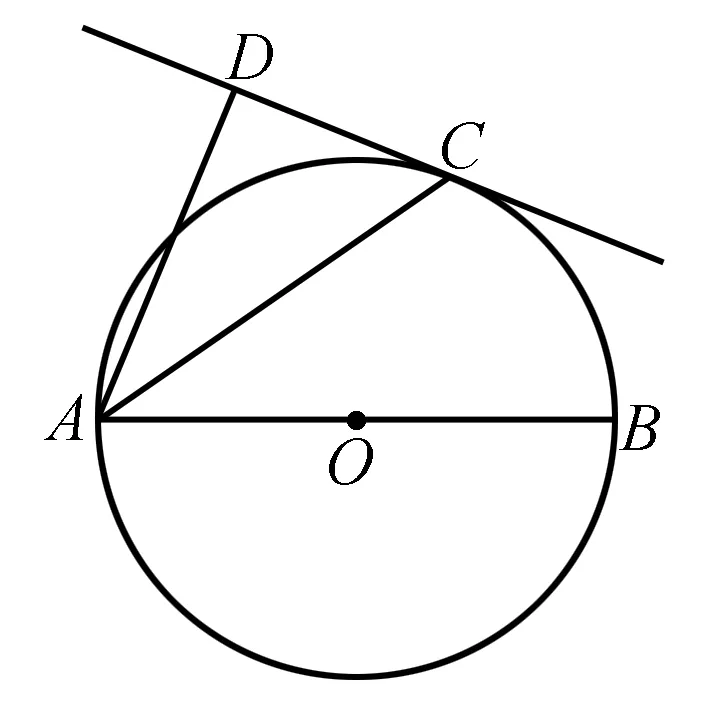
实际上，从归纳推理这一数学思想的本质来看，即是要求学生在思考的过程中学会“由已知推未知”，这同时也是归纳推理思想的核心所在，在初中数学教学过程中要想完成归纳推理思想的渗透，势必要注重对学生“由已知推未知”这一核心思想的训练.众所周知，在初中数学学习中，解答数学应用题是学生的一大弱项，这一问题同时也让数学教师头疼不已，由于初中数学应用题不仅考察学生对于基本数学知识的掌握程度，同时对于学生的综合知识运用能力也有着较高的要求，初中数学应用题一般设置两到三个问题，问题之间衔接性较强，一环扣一环，需要学生具备足够的逻辑推理能力才能完成解答.但总体来说，数学应用题重点考察的便是学生“由已知推未知”的能力，因此在初中数学教学中归纳推理意识的渗透应用时，教师可以选择比较具有代表性数学应用题在课堂之上“以引导为主，讲解为辅”，充分培养学生“由已知推未知”的能力，从而实现归纳推理意识的成功渗透.例如：如图，AB为⊙O的直径，C为⊙O上一点，AD垂直于过C点的直线，垂足为D，AC平分∠DAB．

(1)试判断CD与⊙O的位置关系;

(2)若AD=4，AC=5，求⊙O的半径OA．

针对这一解答题，计算方面并不难，真正的难点是学生很难从中寻找到突破口，这种题目逻辑性很强，一般只要找到推理的点，很多问题都能依据推理迎刃而解.该题目对于问题(1)学生还是可以根据题目隐藏的信息一步步推理出来，问题的难度主要在第(2)问，根据已知的结论学生很难推出圆的半径是多少，没了相关类似(1)的提示学生很难想到利用三角形相似定理进行“迁移”.因此需要学生在该类型问题上拓展自己的思维宽度，本着由已知推未知的想法，一步步进行逻辑推理，这里的“已知”或许不能像第(1)问直接从题意中找到，但实际上“已知”就藏在平时所学习的数学知识中，需要学生充分调动自己的归纳推理思维，可以尝试从不同的角度去连接线段，连线是更要注意类似“半径”、“垂直”等敏感位置的连线，使得问题变得更加清晰明朗起来，从而成功将问题解决.