以课本为本 显探究为真——2018年南通市数学中考一道压轴题的探究过程

杨卫东

(江苏省海门市悦来初级中学 226100)

本文就2018年南通市数学中考第28题(压轴题)的由来及思维宽度、长度、高度、深度的探究过程奉献与大家，以求资源共享、期待思维碰撞.

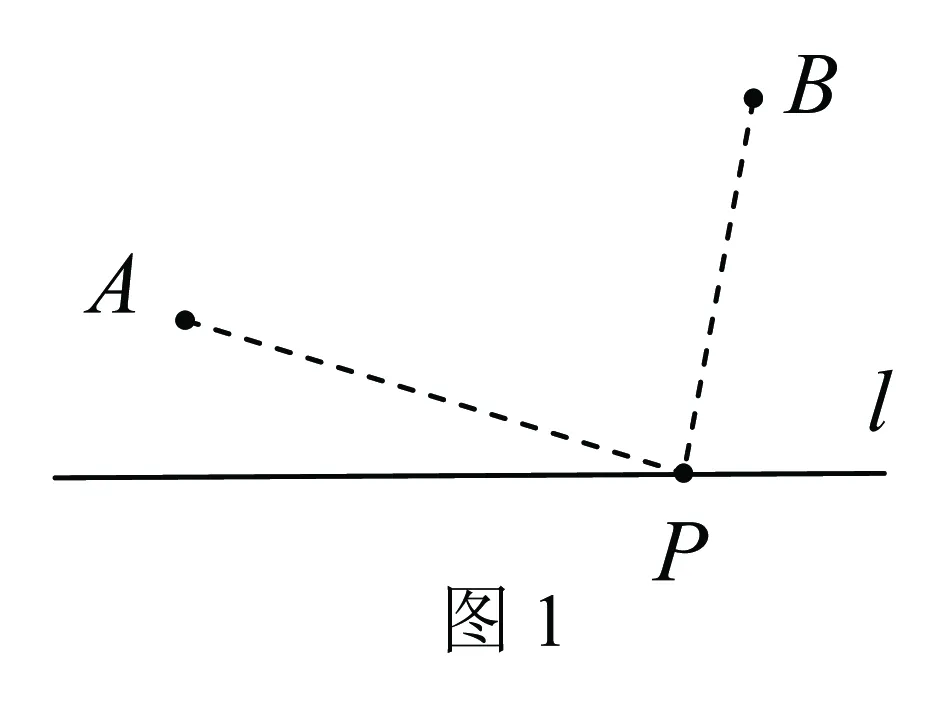
【课源再现】人教版数学教材八年级P85问题1：如图1，牧马人从A地出发，到一条笔直的河边l饮马，然后到B地，牧马人到河边的什么地方饮马，可使所走的路径最短？

【策略分析】1．“两点之间，线段最短”和“垂线段最短”是我们分析、解决最短路径问题的理论依据和转化手段.众所周知：当A′地和B地位于直线l的两侧时(如图2)，只要连接A′B，根据“两点之间，线段最短”，可知A′B与l的交点P就是直线l上能使PA′+PB最小的位置.

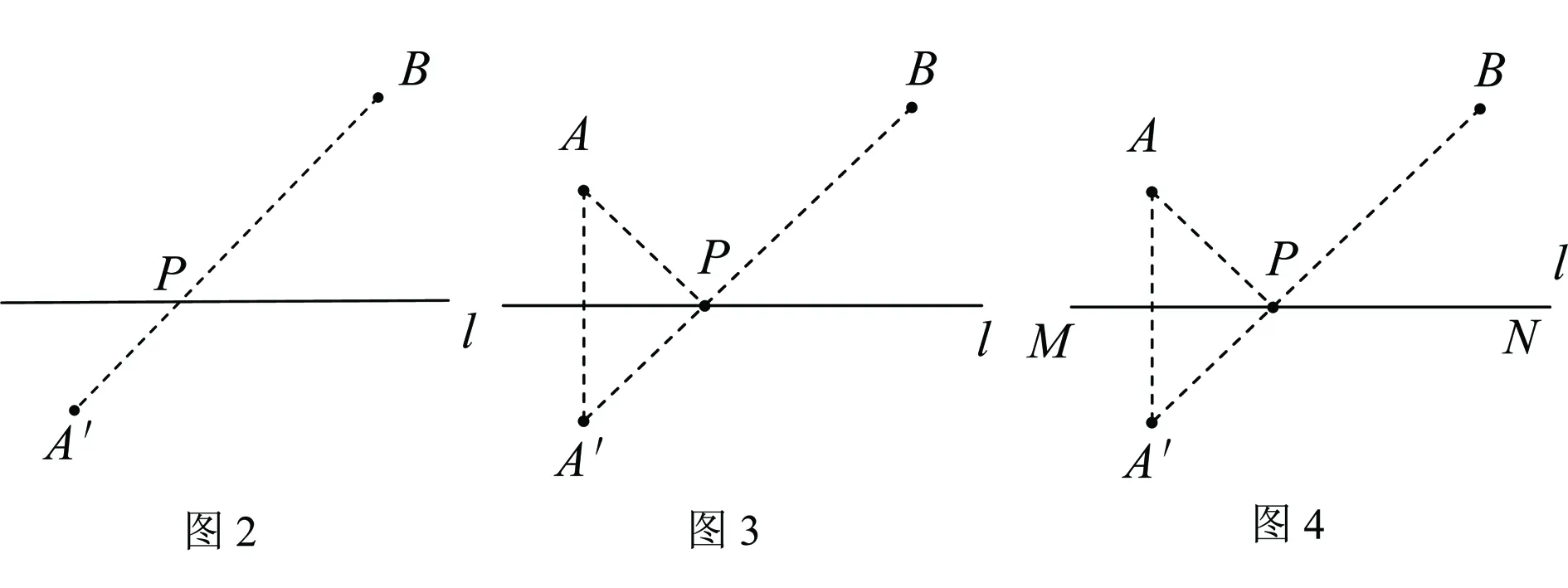
2．如何把图1转化为图2的情况呢？显然，只要在图1中作出点A关于直线l的对称点A′，利用轴对称的性质，可以得到PA=PA′，此时PA+PB=PA′+PB≥A′B，即点P为线段A′B与直线l的交点时，PA+PB最小(如图3).

【经验积累1】在解决最短路径问题时，我们通常利用轴对称、平移、旋转等图形变换把已知问题转化为容易解决的问题，从而作出最短路径的选择.

【潜心识图】如图4，因为PA=PA′，所以∠APM=∠A′PM.因为∠A′PM=∠BPN，故∠APM=∠BPN.过点P再作直线MN的垂线，利用等角的余角相等，即可轻松得出物理学科中“反射角等于入射角”的熟悉结论，让人倍感亲切又添无限遐想——能否把这个图形放在平面直角坐标系中作进一步探究呢？

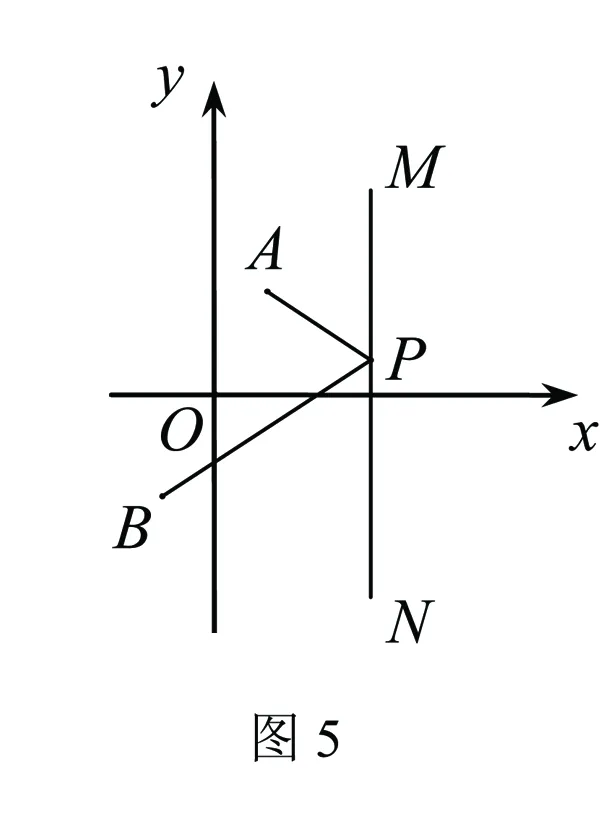
【探究方向1】如图5，在平面直角坐标系xOy中，A，B为直线MN同侧的两点，点P为直线上位于M，N间的任意一点，若锐角∠APM=∠BPN，则称点P为点A，B关于直线MN的“反射点”．

已知点A(1，2)，B(-1，-2)．

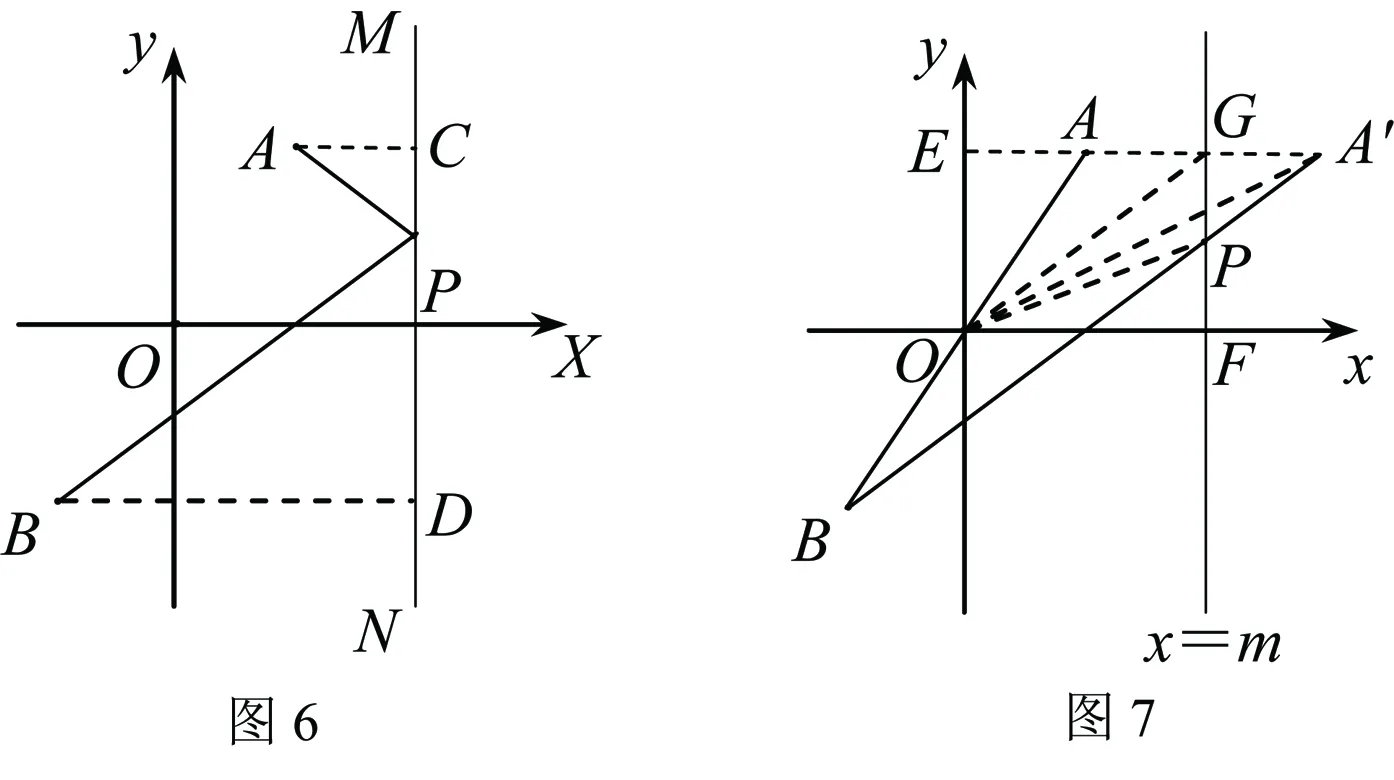
(1)求点A、B关于直线x=m(m>1)的反射点P所在图象的函数解析式．

【灵感一现】虽然直线x=m(m>1)是一条随m的变化而作平移的直线，由于点A，B关于原点中心对称，而且直线x=m∥y轴，那么其反射点P运动所形成的图象是否存在某种特殊性呢？

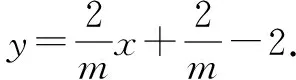
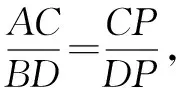
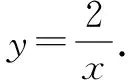
3．面积法：如图7，延长A′A交y轴于点E，直线x=m交A′A于点G，交x轴于点F，连接OG、OA′、OP．

∵AG=GA′，AO=OB,

∴OG∥BA′，S△OAG=S△O A′G,

∴S△OPG=S△O A′G,

∴S△OAG=S△OPG.

∵矩形OEGF中△OEG≌△GFO,

∴S△OEG=S△GFO,

∴S△OEG-S△OAG=S△GFO-S△OPG,

即S△OEA=S△OFP.

∵A(1，2),∴S△OEA=1，∴S△OFP=1.

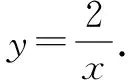
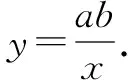
【探究方向2】已知点A(1，2)，B(-1，-2)．

(2)设点P是点A、B关于直线y=2x+n的反射点，当45°≤∠APB≤60°时，直接写出点P的横坐标xp的取值范围．

【灵感二现】虽然直线y=2x+n是一条随n的变化而作平移的直线，但点A，B关于原点中心对称，且直线MN∥AB，那么点A、B关于直线MN的反射点P所在图象又有着怎样特殊的结论呢？

【二证灵感】还得从点P为点A，B关于直线MN的反射点定义出发，同时结合点A，B关于原点中心对称，再利用直线MN∥AB切入较为自然和踏实.

如图8，连接OP，分别过点A，P作AC⊥y轴，PD⊥y轴，垂足分别为C，D，过点A作AE⊥BP，垂足为E，则∠ACO=∠ODP=90°．先从n<0开始研究吧，此时点P在AB的右下方．

∵直线AB的函数解析式为y=2x，而直线MN：y=2x+n，∴AB∥MN,

∴∠APM=∠BAP，∠BPN=∠ABP.

∵点P是A，B关于直线MN的反射点,

∴∠APM=∠BPN,

∴∠BAP=∠ABP∴PA=PB.

∵OA=OB, ∴OP⊥AB,

∴∠AOP=90° ，∠APO=∠BPO.

①当∠APB=45°时，∠OPA=22.5°，∠PAB=∠B=67.5°．

∵∠BEA=∠AOP=90°，∴ △BEA∽△AOP．

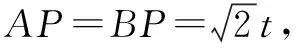
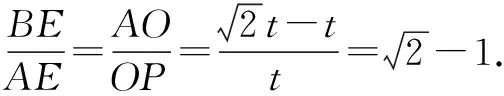
∵∠AOP=90°,

∴∠AOC+∠DOP=∠AOC+∠CAO=90°,

∴∠DOP=∠CAO.∵∠ACO=∠ODP=90°,

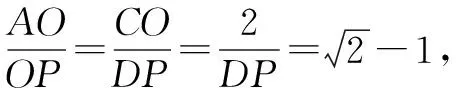
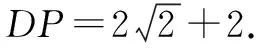
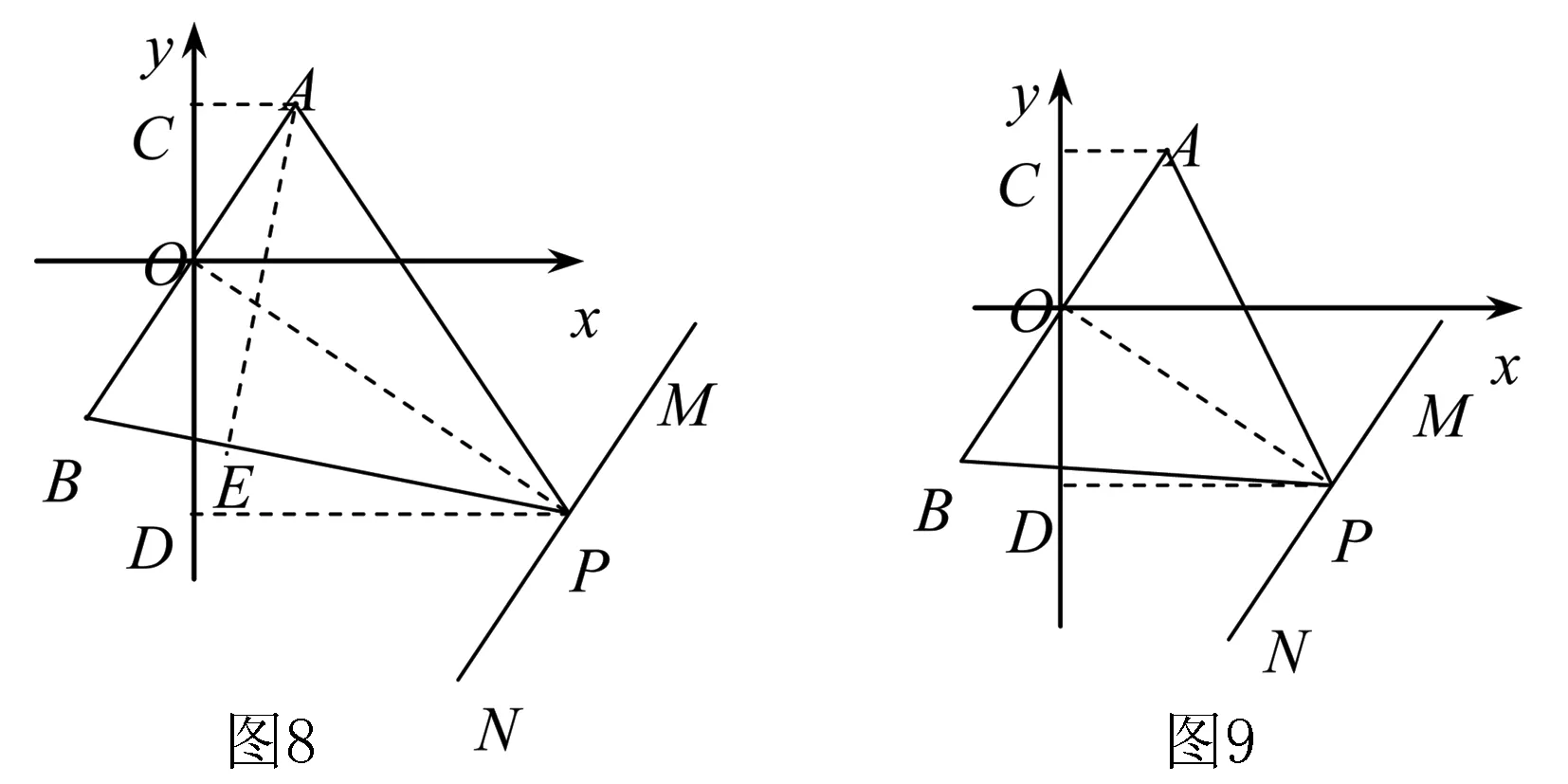
②当∠APB=60°时(如图9)，∠OPA=30°．

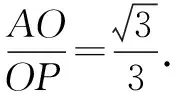
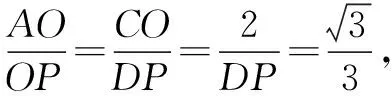
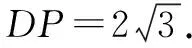
∵45°≤∠APB≤60°,

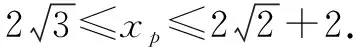
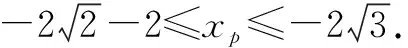
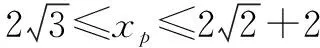
【经验积累3】若点A(a，b)，B(-a，-b)，且a·b≠0，设∠APB=α．

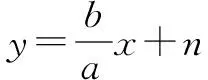
【探究方向3】已知点A(1，2)，B(-1，-2)．

(3)设点P是点A，B关于一次函数y=kx+t(k≠0)的图象的反射点，且点P位于直线AB的右下方，当∠APB=60°时，请直接写出t的取值范围．

【灵感三现】虽然直线MN：y=kx+t(k≠0)的位置千变万化，但有条件∠APB=60°，点A、B关于直线MN的反射点P所在图象又有着怎样的令人惊喜呢？

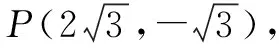
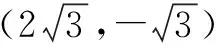
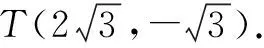
∵k≠2，∴直线MN与AB不平行，只能相交．设直线MN与这个圆交于点T′．

∵∠APM=∠BPM，∠APB=60°，∴∠APM=∠BPM=60°．

根据同弧所对的圆周角相等，得∠BAT′=∠BPN=60°，∠AT′B=∠APB=60°．

∴△ABT′是等边三角形，∴点T′与点T重合．

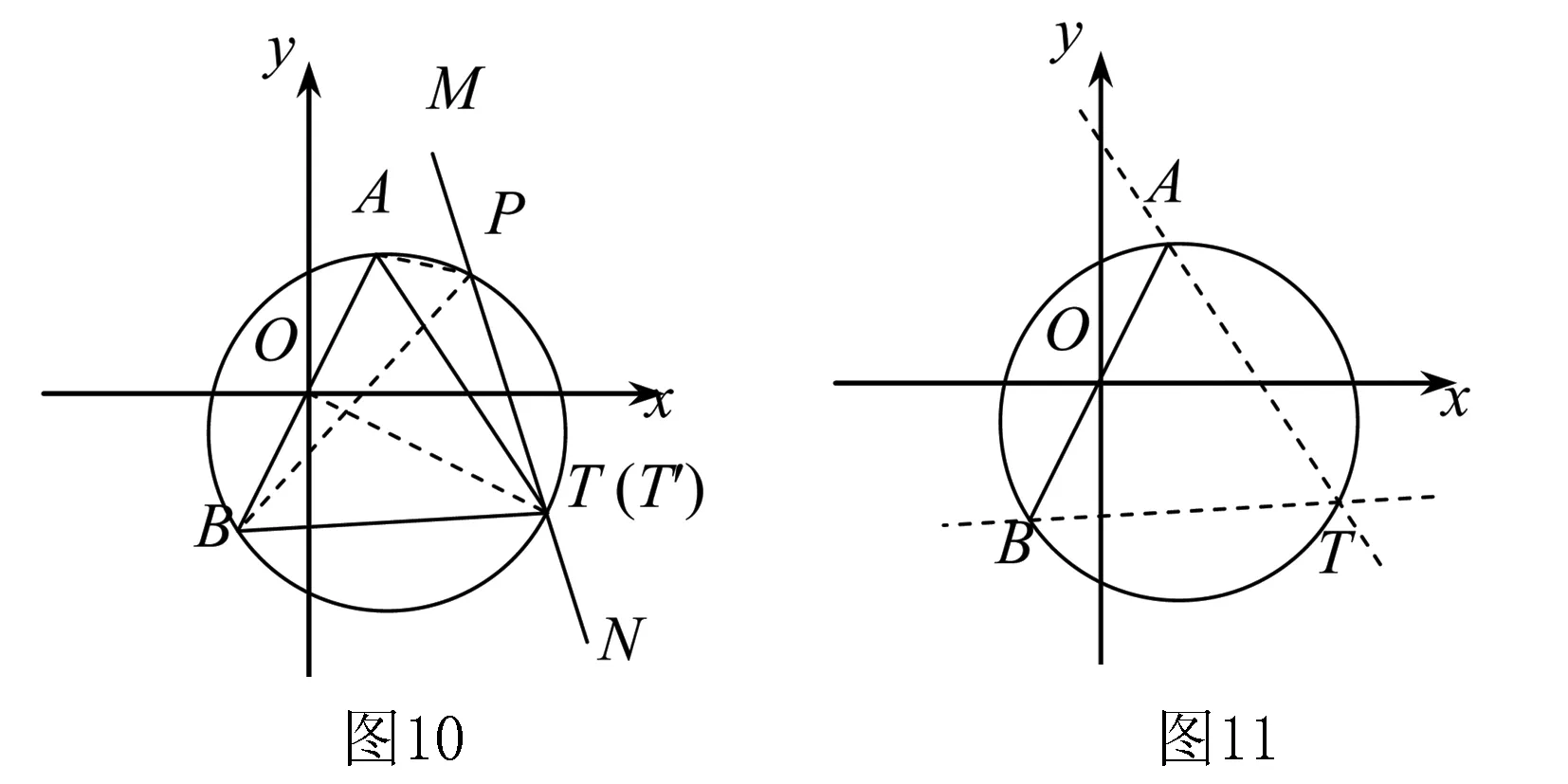
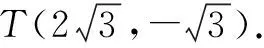
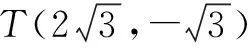
【经验积累4】若点A(a，b)，B(-a，-b)，且a>0，b>0，∠APB=60°．△ABT为正三角形，点T在第三象限.

设点P是点A，B关于一次函数y=kx+t(k≠0)的图象的反射点，且点P位于直线AB的右下方，则点P一定落在△ABT外接圆的优弧ATB上.当然点P既不能与点A、点B重合，也不能和过点T作坐标轴的平行线与优弧ATB的交点重合.至此容易理解：满足题意的一次函数y=kx+t(k≠0)的图象是一条过定点T且可以作适当旋转的直线.

【形成试题】(2018年南通市中考数学第28题)

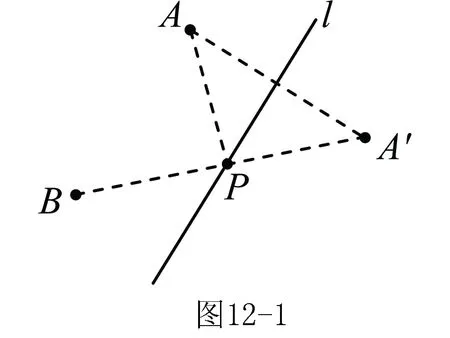
定义：如图12-1，A，B为直线l同侧的两点，过点A作直线l的对称点A′，连接A′B交直线l于点P，连接AP，则称点P为点A，B关于直线l的“等角点”．

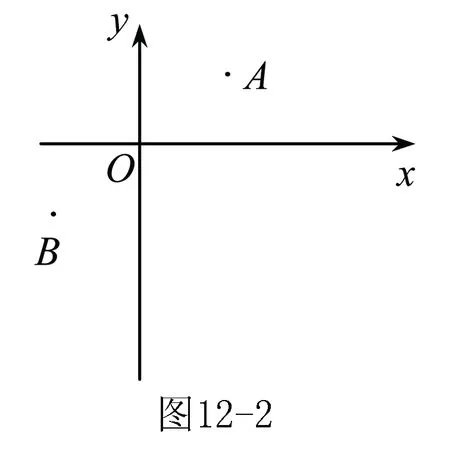
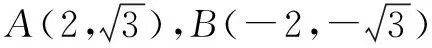
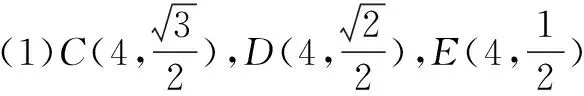
(2)若直线l垂直于x轴，点P(m，n)是点A，B关于直线l的等角点，其中m>2，∠APB=α，

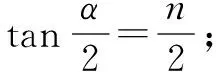
(3)若点P是点A，B关于直线y=ax+b(a≠0)的等角点，且点P位于直线AB的右下方，当∠APB=60°时，求b的取值范围(直接写出结果)．

【意犹未尽】图5中，如果我们换一个角度去思考：PA+PB的最小值是否同样存在着探究的方向和灵感所在呢？譬如在已知点A(1，2)和B(-1，-2)的条件下，(1)当直线MN∥AB时，PA+PB的值与∠APB的大小有着怎样的关系？(2)当∠APB=60°时，PA+PB的取值范围是多少？

只要“课本与探究”无缝对接——那是因为我们时常用好教材的同时，需要把数学核心思想渗透到学生自主学习的各个领域，让以学为中心作为支撑点，让逐步养成探究的习惯作为平衡点，那么“减负与增效”必定同步奔跑、同时给力！