化归思想在初中数学解题中的应用

王保成

(浙江省杭州市余杭区太炎中学 311121)

随着新课改教学理念的深入推行，要求在初中数学教学中注重对数学思想的渗透教学，以培养学生具有较高的数学应用能力.在中学数学教学中，常用的数学思想有：化归思想、数形结合思想、函数与方程思想、分类讨论思想等，这些基本的数学思想都可以看成是由化归思想演变而来的，因此，加强化归数学思想在数学教学中的应用，对增强学生灵活的数学思维能力，提高学生数学核心素养具有重要的作用.同时，化归思想的应用有利于将复杂、抽象、不易解决的数学问题转变为简单、形象、易解决的数学问题，从而能够提高学生的数学解题能力和数学解题效率.笔者结合实践数学教学实践，对化归思想在实践数学解题中的应用方法进行了深入探索.

一、化归应用遵循的基本原则

在初中数学教学中，进行化归思想教学与应用，应遵循如下基本原则：

一是简单化的原则.就是化归思想在解题应用中，要遵循把复杂、抽象、困难的问题变为简单、直观、易处理的问题，将特殊类型的数学问题转化成一般类型的问题来解决，要把复杂的大问题转化成多个简单的小问题来处理，以采用简单的方法来各个击破，化归思想方法的应用要能降低解题难度，这样才能更好发挥化归思想的作用.

二是熟悉化的原则.化归思想的运用，要有利于学生将不熟悉的问题转变成熟悉的问题来解决，这样才能让学生利用已有的知识和经验，来快速有效解决遇到的新问题和陌生问题，能帮助学生提高数学解题效率.

三是正难则反的原则.当某些数学问题如果从正面进行解决比较困难时，就可以运用化归的思想，从问题的相反面进行寻找解决的方法，来使问题得到解决.如，在解决数学问题时遇到“至少”、“最多”、“不存在”等问题时，从相反面进行解决就能使问题变得简化.

四是直观化的原则.坚持直观化的原则，就是化归思想在运用中要注重把抽象复杂的问题，尽可能转化成简单易懂的图形来处理，也就是把“数”的问题转化成“形”的问题，注重与数形结合思想的结合运用，使问题变得一目了然，有利于学生快速形成解题思路.

五是极端与标准化的原则.通过对一些问题在极端状态下的特点、特性进行观察来获得有益的解题启示，从中找出所要解决问题在一般状态下的性质，以找到解决问题的思路和方法；化归思想的运用还应坚持标准化的原则，即把特殊或非标准问题尽可能转化成标准人的问题来解决.

二、化归思想的解题应用方法

1.化难为易

在初中数学解题中，许多问题如果按照常规的解题方法来处理就比较复杂，或是不容易找到解题的思路和方法.如果运用化归的思想，把这些复杂的数学问题转化成简单的问题来处理，就非常容易解决.因此，在解题中当遇到复杂问题时，应考虑把问题进行转化以寻求用简单的方法来解决.

解析对于此题的一般解决策略，就是要假设x=2k,y=3k,z=4k，把这三个式子代入到所求分式中来进行计算，该方法是把多元的分式转化成了一元的方法，在解题中仍然比较复杂而且容易出现错误.如果将三个未知数用三个特殊数字来代替：x=2,y=3,z=4，这样就能既简单又快速地求出分式的数值.该方法的运用要注意题目的特点和所给条件的合理恰当使用，主要用于寻找解题思路和方法使用.

2.化数为形

在初中数学解题中，对于一些数量关系比较复杂抽象的问题，如果能把这些复杂的数量问题变成直观的几何图形问题就能让学生容易解决问题，而且还可以绕开冗长繁琐的数量计算过程.

例2 已知x>0，求代数式：x2+4+(12-x)2+9的最小值是多少.

解析本题属于代数题目，但对于初中学生来说，不容易用代数方法直接解答本题，如果能够变换解题思路，运用数形结合的方法，把代数问题转化成几何问题来求解，就容易解决.可以根据勾股定理，来构造两个直角三角形，并把x2+4和(12-x)2+9当成是两个直角三角形的斜边.因为BD=12，设BE=x，可以把这两个直角三角形的一条直角边放在同一条线段上,根据三角形两边之和大于第三边，即：AE+EC>AC，当A,E,C三点在一条直线上时最小.如图1所示，这样就把代数问题转化成了求两条线段之和最短的问题了.即求图中的AE+EC的最小值，由于两点之间的线段是其最小值，这样就能在直角三角形AFC中容易求出代数式的最小值是13(即AC长).

3.化动为静

在初中数学解题中，特别是在中考解题时，许多学生对于综合性的动态题目经常是不知如何下手，不易找到解题的思路和方法.如果运用化归的思想，把动态的问题想法转化成静态问题，这样问题就变得容易解决了.

例3 在图2所示直角三角形ACB中，已知AC=6，BC=8，M点是斜边AB上的动点(不与A、B重合)，E是直角边BC上的中点，作一个直角，MF和BC相交于F点.假设BM=x，△BME的面积是y，求出：y关于x的函数关系式，并确定x的取职范围.

4.化斜为直

在初中的平面几何解题中，经常遇到解斜三角形的问题，当已知一个三角形的下列情况的边与角的数据时就能确定该三角形：三条边、两边及夹角、两角及夹边、两角及对边.在现实生活中许多问题是以斜三角形为背景，在解决这类问题时，如果通过作三角形的高线，就能把斜三角形的问题转化成直角三角形的问题，这样就容易求解三角形的问题.

例4 在图3中要从A地到B地，因为在两地之间有一座山，需要绕行到C地，再从C地到达B地，现在要在山中开挖一条隧道，这样就可从A地直接通行到B地.已知AC距离是20km，∠A=30°，∠B=45°，求从A地直接通达B地比原来路程少走多少km.

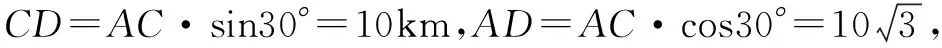
5.化整为零

在初中数学解题中，运用化整为零的方法可以把某些复杂的综合性问题化归成若干个独立简单容易解决的小问题，通过对这些小问题的解决，就能够实现对整个题目的求解.

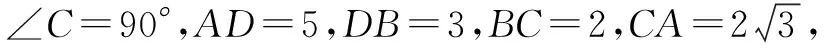
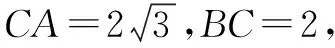
综上所述，化归数学思想贯穿在中学数学学习的全过程，加强对化归思想的教学渗透，能有效地培养学生灵活的数学思维能力，能把复杂、抽象、不熟悉、不易解决的问题转变为简单、直观、熟悉、易解决的问题，能够降低解题的难度，提高数学解题的效率和准确率，对培养学生较高的数学核心素养具有重要意义.