否定非对合剩余格的IV-模糊理想
刘春辉
赤峰学院 数学与统计学院,内蒙古 赤峰 024000
1 引言
剩余格是由Ward和Dilworth于20世纪30年代在文献[1]中首次提出的一类重要且应用广泛的代数系统,它是Heyting代数的合理推广。目前,这一代数系统已经被学者们公认为模糊逻辑研究中理想的代数框架之一,相关研究成果颇为丰富[2-8]。1965年,Zadeh创立了模糊集理论[9]。Rosenfeld提出了模糊子群的概念[10],标志着模糊代数研究工作的开始。随后模糊集理论被广泛应用于各类代数系统的研究,并取得了丰富的研究成果[11-20]。其中,文献[21]将模糊集思想应用于否定非对合剩余格,给出了否定非对合剩余格的模糊理想和模糊素理想的概念,获得了否定非对合剩余格的模糊理想和模糊素理想的若干性质和等价刻画。作为对模糊集概念的推广,1975年,Zadeh在文献[22]又提出了区间值模糊集(Interval Valued fuzzy set,简记为IV-模糊集),文献[23]讨论了半群的IV-模糊理想,文献[24]研究了R0-代数的IV-模糊子代数,文献[25]研究了Fuzzy蕴涵代数的IV-模糊滤子。本文将IV-模糊集思想应用于否定非对合剩余格的理想问题的研究,给出了否定非对合剩余格的IV-模糊理想的概念,讨论了其相关性质,为进一步深入研究否定非对合剩余格的结构创造了条件。
定义1[1]设L是一个集合,称(2,2,2,2,0,0)型代数是一个剩余格,简称L是一个剩余格,若对任意x,y,z∈L下列各条件成立:
引理1[1-8,21]设L是一个否定非对合剩余格,则下列各结论成立,其中∀x,y,z∈L


引理2[8,21]设L是一个否定非对合剩余格,在L上定义二元运算满足:

则下列各结论成立,其中∀x,y,z∈L

定义2[7]设L和M是两个否定非对合剩余格,f:L→M为映射。若对任意x1,x2∈L有:

定义3[9]设L是一个否定非对合剩余格,则L上的一个模糊集A指的是映射A:L→[0,1]。
定义4[21]设L是一个否定非对合剩余格,A是L上的模糊集,若对任意的x,y∈L满足:
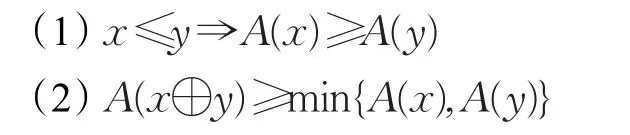
则称A是L的模糊理想。

并且规定D[0,1]中元素的大小关系为:

设X是非空集合,X上的一个区间值模糊集(简记为IV-模糊集)定义为:

2 否定非对合剩余格的IV-模糊理想
定义5设L是一个否定非对合剩余格是L上的IV-模糊集,若对任意的x,y∈L满足:
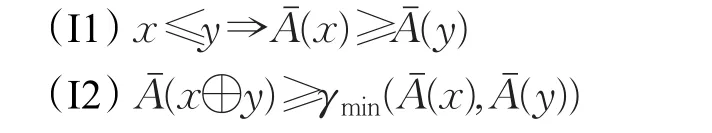
例1设L={0,a,b,c,d,e,f,1}满足且b 表1 L上二元运算的定义 表1 L上二元运算的定义 0abcdef 1 000000000 a0aaa0aaa b0aab0aab c0abc0abc d0000dddd e0aaadeee f 0aabdeef 10abcdef 1 表2 L上二元运算→的定义 命题1设L是一个否定非对合剩余格,如果IVFI(L),则对任意x,y∈L,下列等式成立: 证明设因为故由(I1)得又因为且所以又得命题得证。 定理1设L是一个否定非对合剩余格,是L上的IV-模糊集,则当且仅当对任意的 x,y∈L,满足: 证明设对任意的x,y∈L,因为0≤x,所以由(I1)得,即(I3)成立。又因为由的定义和(P4)得,所以由(P1)得从而由(I1)和(I2)得,即(I4)亦成立。 反之,设(I3)和(I4)成立且 x,y∈L。若 x≤y,则由(P5)得 y′≤x′,从而,所以,故满足(I1)。 又 因 为,所 以,故由(I4)得,故亦ˉ满足(I2)。因此,由定义5得 定理2设L是一个否定非对合剩余格,是L上的IV-模糊集,则当且仅当对任意的 x,y∈L,满足: 证明设,则由定理1得(I3)成立。任取 x,y∈L,由(P6)和(P9)得故由(I1)得所以由(I4)得,因此,Aˉ亦满足(I5)。 反之,假设(I3)和(I5)成立,则在(I5)中取 y=x″得。任取 x,y∈L ,因为由(P9)得′,所以由(I5)便得 命题2设L是一个否定非对合剩余格,如果IVFI(L),则对任意 证明设,任取 x∈L,则由(P6)和(I1)得,而由定理2的证明又得因此 定理3设L是一个否定非对合剩余格,是L上的IV-模糊集,则当且仅当和都是L的模糊理想。 证明设是 L 的IV-模糊理想,且任取x,y∈L。一方面,若 x≤y,则由(I1)得从而且 另一方面,由(I2)得 所以由区间数的大小关系定义得 故由区间数的大小关系定义得 另一方面,由定义4(2)得 故由区间数的大小关系定义又得 定义6设X是非空集合,设和是X上的两个IV-模糊集,定义IV-模糊集为: 称之为IV-模糊集Aˉ和Bˉ的交。 定理4设L是一个否定非对合剩余格,和Bˉ是L 上的两个IV-模糊集。若,则IVFI(L)。 证明设且 ∀x,y∈L 。一方面,若x≤y ,则由(I1)得且,从而由定义6得 于是,再由定义6得 定义7设X和Y是两非空集合,分别是X和Y 上的IV-模糊集,对任意(x,y)∈X×Y ,定义映射满足: 引理3设L和M是两个否定非对合剩余格,在L×M 上逐点定义四种运算满足:对任意(x1,y1),(x2,y2)∈L×M ,规定 则L×M关于上述四种运算构成一个否定非对合剩余格,称之为L和M的乘积否定非对合剩余格。 定理5设L和M是两个否定非对合剩余格,IVFI(L)且,则 证明设,则对任意(x1,y1),(x2,y2)∈L×M,若(x1,y1)≤(x2,y2),则且,并且有: 定理6设L和M是两个否定非对合剩余格是L上的IV-模糊集,f:L→M 为同构映射。若IVFI(L),则,其中 证明设 f是L到M的同构映射,对于任意的y1,y2∈M ,由 f是满射知存在 x1,x2∈L使 f(x1)=y1且f(x2)=y2。 一方面,若y1≤y2,则从而由 f为单射得进而 x1≤x2,故由及(I1)得,于是 于是 定理7设L和M是两个否定非对合剩余格,Bˉ是L上的IV-模糊集,f:L→M为单调递增的同态映射。若,则,其中 证明设,任取 x1,x2∈L,若 x1≤x2,则由 f单调递增得 f(x1)≤f(x2),从而再由 f为同态映射及(I1)得 将IV-模糊集的思想应用于否定非对合剩余格理想问题的研究,引入了否定非对合剩余格的IV-模糊理想的概念,详细讨论了其性质特征,获得了若干有意义的结论。值得注意的是,诸如BL代数、MTL代数、MV代数格蕴涵代数、R0代数等著名的模糊逻辑代数都是否定非对合剩余格的特例,因此,可以说上述结果是这诸多逻辑代数共同特征的体现。此外,本文工作在有效拓展IV-模糊集理论的应用领域的同时,也为进一步深入研究否定非对合剩余格的结构创造了条件。



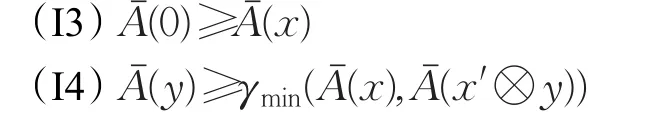




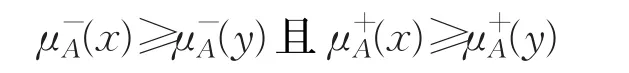


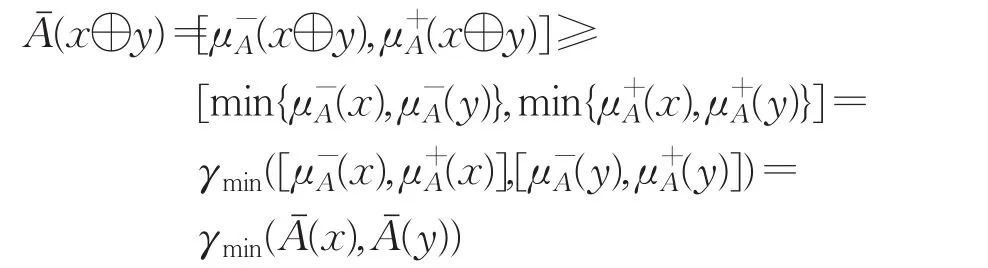
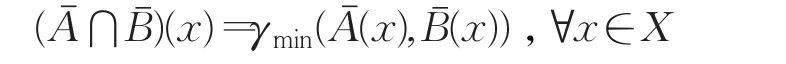
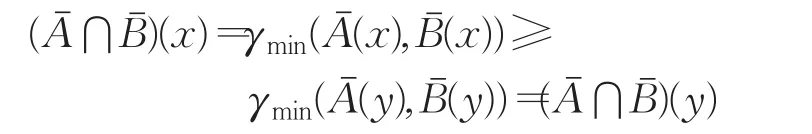


3 IV-模糊理想的直积和同态性质

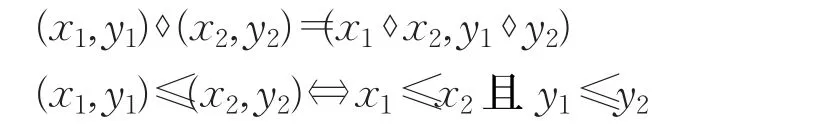










4 结束语

