布谷鸟搜索算法综述

张晓凤，王秀英

青岛科技大学 信息科学技术学院，山东 青岛 266000

1 引言

群智能算法以其简单灵活，易于实现，并在实际应用中取得了有效成果而备受研究者们的青睐。受布谷鸟巢寄生育雏行为的启发，Yang等[1]于2009年提出了一种新型的群智能优化算法：布谷鸟搜索（Cuckoo Search，CS）算法。CS算法通过模拟布谷鸟巢寄生育雏行为，结合鸟类、果蝇等的Lévy flights机制进行寻优操作，能够快速有效地找到问题的最优解。CS算法的关键参数仅为外来鸟蛋被发现的概率和种群数目，整个算法操作简单、易于实现。CS算法利用莱维飞行进行全局搜索，具有良好的全局寻优能力。作为一种通用型算法，CS算法易于与其他算法相结合，进而获得性能更加优越的混合算法。

自CS算法被提出以来，国内外学者对其进行了大量的研究。文献[2]建立了CS算法的Markov链模型，对算法的收敛性进行了分析，通过仿真实验验证了CS能够收敛于全局最优；文献[3]使用模糊系统来动态调整CS算法的参数，分析了参数对CS算法性能的影响。CS算法的变体及其应用研究也得到了快速发展，文献[4]对CS算法及其变体最初的发展进行了综述，但没有进行详细的介绍。目前CS算法的理论研究比较零散，尚未形成体系。本文在综述国内外相关研究成果的基础上，对CS算法及其变体和应用进行比较全面的综述，并指出CS算法未来值得关注的研究方向，为研究者们深入研究CS算法提供借鉴。

2 布谷鸟巢寄生育雏行为和莱维飞行

2.1 巢寄生育雏

布谷鸟是典型的具有巢寄生育雏行为的鸟类。某些种属布谷鸟自己不筑巢、不孵卵、不育雏，而是偷偷地将卵产在其他鸟（宿主）的鸟巢中，由宿主代为孵化和育雏。

布谷鸟在繁殖期间，首先寻找繁殖期和育雏期与自己相近、雏鸟饮食习惯相似、卵形状和颜色基本相同的鸟类作为宿主。然后，趁宿主外出时迅速将自己的卵偷偷产入宿主的鸟巢中。为了不被宿主察觉，布谷鸟在产卵之前会把宿主鸟巢中的一枚或多枚卵移走，来保持鸟巢中原有的卵数量。一旦布谷鸟的寄生卵被发现，这个卵便会被鸟巢主人移走，布谷鸟寄生繁殖失败。

2.2 莱维飞行

莱维飞行本质上是一种随机游走过程，由高频率的短距离飞行和低频率的长距离飞行组成，它的步长服从莱维分布。

在自然界中，许多鸟类的飞行行为都具有典型的莱维飞行特征。布谷鸟在飞行过程中，主要以小步长的短距离飞行为主，但是偶尔有比较大步长的长距离飞行，因此布谷鸟不会停留在一个地方重复进行搜索。搜索前期，大步长有利于增加种群多样性，扩大搜索范围，易于搜索到全局最优；搜索后期，小步长有利于提高搜索精度，缩小搜索范围，使得在小范围内收敛于全局最优解。

3 布谷鸟搜索算法

3.1 标准CS算法介绍

在自然界中，布谷鸟以随机或者类似随机的飞行方式来寻找适合自己产卵的鸟巢的位置，为了便于模拟布谷鸟的繁殖策略，Yang等[1]将布谷鸟算法假设以下三个理想状态：

（1）每只布谷鸟一次只产一个卵，并随机选择一个位置的鸟巢进行孵化。

（2）在随机选择的一组鸟巢中，质优的鸟巢将会被保留到下一代。

（3）可利用的鸟巢数量固定，鸟巢主人发现外来鸟蛋的概率为Pa∈[0,1]。当鸟巢主人发现外来的布谷鸟蛋的时候，它会将布谷鸟蛋丢弃或者重新建立新的鸟巢。

基于以上三个理想状态，布谷鸟寻找宿主鸟巢的位置和路径的更新公式如下：

其中

通过公式（1）进行位置更新后，生成随机数r(r∈[0,1])，并将r与Pa进行比较，如果r＞pa，就随机更新一次鸟窝位置，否则鸟巢位置不变。

根据上述过程，布谷鸟算法的实现过程如下：

步骤1初始化：设置种群规模、搜索空间维数和最大迭代次数等参数。随机初始化鸟巢的位置Xi，i∈[1,n]，定义目标函数 f(X),X=[X1,X2,…,Xn]T。

步骤2计算每个鸟巢位置的目标函数值并进行比较，得到当前的最优函数值。

步骤3利用莱维飞行（式（1））对除最优鸟巢以外的其他鸟巢的位置和状态进行更新，计算目标函数值，获得的函数值与当前的最优函数值进行比较，若较好，则更新记录当前最优值。

步骤4位置更新后，用随机数r与Pa进行比较，如果r＞pa就随机更新一次鸟窝位置，否则鸟巢位置不变。

步骤5若满足最大迭代代数或搜索精度要求，继续下一步，否则转回步骤3。

步骤6输出全局最优鸟巢的位置。

3.2 CS算法特性分析

3.2.1 CS算法与其他算法的比较

文献[5]通过50多个基准测试函数进行测试，对CS、粒子群优化算法（PSO）和人工蜂群（ABC）算法的性能进行了对比分析；文献[6]利用标准测试函数，对CS和萤火虫（FA）等算法的精确度和稳定性进行了对比分析；文献[7]对CS、FA和果蝇优化算法（FOA）等多种群智能算法的优缺点进行了比较；文献[8]也对FA、ABC、PSO以及蚁群算法（ACO）等多种群智能算法的性能进行了比较。综合以上文献研究，对几种典型的群智能优化算法进行比较，如表1所示。

由表1可以看出，与其他算法相比，CS算法具有全局寻优能力强，参数少且易于实现，易与其他算法相结合等综合优势，但同时也存在收敛速度慢、进化后期种群多样性差等不足。

3.2.2CS算法的有效性分析

（1）CS算法参数较少：除了种群规模之外，CS算法基本上只有一个参数Pa需要调整。而算法的收敛速度对参数Pa不敏感[1]，这意味着CS算法的通用性很好，鲁棒性较强。

（2）CS能够满足全局收敛性要求：王凡等[2]的理论研究已经证明CS算法具有全局收敛性。

（3）CS算法具有局部搜索和全局搜索能力[9]：局部搜索通过定向地随机游走能够改善最优解，全局搜索通过莱维飞行来保持种群的多样性。随机搜索的两个分量之间的平衡由切换概率Pa控制，使得CS能够在全局范围内更有效地探索搜索空间，从而有效保持种群多样性。

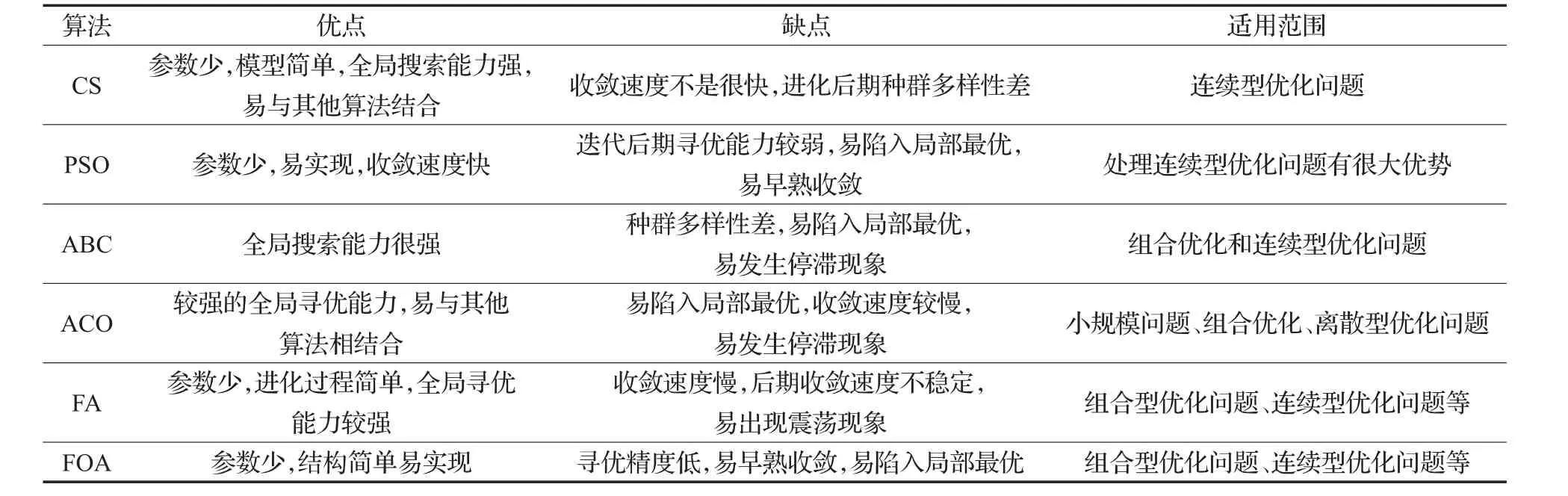
表1 CS算法与其他算法的比较

（4）CS的另一个特点是利用莱维飞行进行全局搜索，而不是基于高斯过程的标准随机游走。莱维飞行具有无限的均值和方差，保证CS算法更加有效地探索搜索空间，因此能够更加高效地发现全局最优。

3.2.3 CS算法的缺陷

（1）CS算法收敛速度偏慢、求解精度较低：CS算法通过莱维飞行机制寻找鸟巢，莱维飞行是一种由小步长的短距离飞行和偶尔大步长的长距离飞行组成的随机游走过程，因此布谷鸟的寻窝路径容易在不同的搜索区域间跳跃，导致布谷鸟算法的局部精细搜索能力较差，在算法迭代后期容易在全局最优解附近的区域出现震荡现象，造成算法效率偏低。

（2）CS算法只能用于求解连续型优化问题，对于离散型、约束型、组合型以及多目标优化问题，需要更进一步的研究。

4 CS算法的变体

为了提升CS算法的性能，扩展CS算法的应用领域，研究者们开发了多种CS算法的变体，例如用于求解离散型优化问题的二进制CS算法、离散型CS算法；用于改善CS算法性能的混沌CS算法、自适应CS算法以及与其他算法的混合；用于求解多目标优化问题的多目标CS算法。下面具体介绍CS算法的变体。

4.1 二进制CS算法

Gherboudj等[10]提出了一种离散二进制布谷鸟搜索（Binary Cuckoo Search，BCS）算法来处理二进制优化问题，使用sigmoid函数和概率模型来生成二进制解。在一些背包问题实例和多维背包问题实例上进行测试，与和声搜索算法、粒子群算法和量子CS算法相比，BCS在寻找全局最优方面效率更高。但是BCS算法的收敛速度对其参数不敏感，未来可以通过引入最佳解决方案之间的信息交换来加以改进，以加快BCS的收敛速度。

Rodrigues等[11]提出了用于特征选择的二进制布谷鸟搜索算法（BCS）。搜索空间被建模为n维布尔点阵，解决方案在超立方体的角点处进行更新，采用解决方案的二进制向量，其中1对应一个特性被选择来组成新的数据集，否则为0。在从巴西电力公司获得的两个数据集上进行测试，证明了BCS用于特征选择是有效的，BCS的鲁棒性优于二进制蝙蝠算法（BBA）、二进制萤火虫算法（BBFA）、二进制重力搜索算法（BGSA）和二进制粒子群优化算法（BPSO），但算法耗时高于BBA。

冯登科等[12]受二进制粒子群算法的启发，对布谷鸟算法进行了二进制改进：用二进制编码串表示鸟巢的位置，对布谷鸟寻找新鸟巢的Lévy飞行路径进行二进制代码变换，引入二进制编码控制系数对二进制编码进行混合更新。利用改进后的算法对背包问题进行求解，获得了优于遗传算法（GA）和几种混合GA的解；用于求解旅行商问题，结果好于GA、ACO和微粒群算法，但略差于叶安新改进的惯性权重自适应调整微粒群算法。

4.2 离散CS算法

Ouyang等[13]提出了离散布谷鸟搜索算法（DCS），用于求解球形旅行商问题（TSP）。将学习算子，“A”算子和3-opt算子应用于公告板中的解决方案，来提高算法的收敛速度。实验结果表明，DCS优于遗传算法。

Ouaarab等[14]提出了改进的离散CS（DCS），通过重建其种群并引入新的布谷鸟种类来扩展和改进CS，改进后的CS被离散化，用于求解旅行商问题。实验证明DCS的性能优于对比算法。但由于未考虑参数对算法性能的影响，无法对DCS算法进行相关性能比较，该算法有待进一步研究和完善。

Bibiks等[15]利用离散布谷鸟搜索（DCS）算法求解资源约束项目调度问题（RCPSP）。在DCS中，鸟蛋代表组合空间中的解，可以用序列来表示，因此搜索空间是一组序列，根据组件的排列顺序将这些序列定位在搜索空间中；通过改变组件的顺序来完成在搜索空间中的移动，步长的大小由莱维飞行决定。实验表明DCS在解的质量和运行时间方面优于对比算法，但是提升的效果并不明显。

王超等[16]提出了离散CS算法（DCS），用于解决带时间窗和同时取送货的车辆路径问题。基于标准CS算法，在莱维飞行位置更新的过程中，通过路径内搜索2-opt法和路径间搜索swap/shift法对当前的鸟巢进行改进；在寄生鸟巢位置更新过程中，通过路径内搜索relocate/exchange法和路径间搜索GENE法来随机产生新鸟巢。在中小型顾客规模算例中，DCS取得了所有算例的最优解，但是在大型顾客规模算例中，DCS并没有显著的优势。

4.3 混沌CS算法

马英辉等[17]引入Tent映射的混沌序列对CS算法进行优化，用改进后的CS算法来搜索二维Renyi灰度熵的最佳阈值来完成图像分割。实验表明，该算法提高了图像分割的精度，提升算法的运算速度。未来的研究可以考虑不同的混沌映射对算法性能的影响，更好地提升算法的性能。

Wang等[18]将混沌理论引入CS算法，使用12个混沌映射来调整CS的步长，提出了一种新颖的混沌布谷鸟搜索（CCS）优化算法。实验证明，改进的CCS显著提高了算法的全局搜索能力及求解的质量。未来可以将CCS用于解决实际工程问题。

Boushaki等[19]提出了一种新的量子混沌CS算法（QCCS），用于解决数据聚类问题。利用混沌映射进行种群初始化，解决初始种群的随机性问题；通过非均匀量子更新技术来改善搜索过程，提高算法的全局搜索能力；此外，还制定了有效的战略来管理边界。实验表明，QCCS增加了种群多样性，有效地提高了边界空间的利用率，加快算法收敛速度。但是在某些数据集中，收敛速度仍然较慢，算法易陷入局部最优。

牛海帆等[20]将混沌理论引入CS算法中，来改善算法在迭代后期收敛速度慢、收敛精度不高和易陷入局部最优等缺点，提出了混沌CS算法（CCS）。首先，利用Logistic映射来初始化种群，增加了种群的多样性；此外，通过引入混沌扰动算子来跳出局部最优，从而完成全局寻优。将CCS算法应用于谐波估计，结果表明，与基于PSO算法的谐波估计方法相比，CCS具有更高的估计精度，尤其是对直流衰减分量的时间常数的估计。但是CCS算法并没有在总体变量上得到优化。

4.4 自适应CS算法

Li等[21]提出了改进的参数自适应布谷鸟搜索算法。受DE算法的启发，在CS算法的整个种群中使用基于rand和最佳个体的两个新突变规则，为了平衡算法的局部搜索和全局寻优，将新规则通过线性递减概率规则进行组合。然后，基于前两个新参数的相对成功数，引入自适应参数设置作为均匀随机数来增强种群的多样性。实验证明，改进后的的算法能有效避免陷入局部最优，显著减少进化过程并提高收敛速度。

Mlakar等[22]提出了一种混合自适应CS算法（HSA-CS），在原始CS算法的基础上添加三种机制：CS算法的参数自适应机制、在CS搜索过程中平衡随机勘探策略的机制、种群的线性减少策略。基于基准测试函数，验证了算法的有效性。但与对比算法进行比较，优化效果并没有明显的提升，且HSA-CS采用平衡概率的确定性设置，需要大量的工作来确定该参数的最佳值。

Jaballah等[23]提出了一种自适应布谷鸟搜索算法（SACS），其中控制参数根据优化过程的演变进行动态调整。利用SACS求解射频识别（RFID）网络规划问题，结果表明，SACS获得优于其他自适应CS算法的解决方案。但对比算法只有CS及其变体，无法全面验证SACS的性能。

4.5 多目标CS算法

Yang等[24]提出了多目标布谷鸟搜索算法（MOCS），将CS算法拓展到多目标优化领域。为了满足多目标优化问题的需求，对标准CS算法的第一条和第三条规则做如下修改：每只布谷鸟一次产K个蛋，并将它们放入随机选择的鸟巢中，第K个蛋对应于第K个目标的解决方案；根据蛋的相似性/差异性，每个鸟巢将以概率Pa被抛弃，并且将建立具有K个蛋的新巢。基于一组多目标测试函数，验证了MOCS算法的有效性。但MOCS算法仍存在收敛速度慢、收敛精度不高的缺陷，针对实际的优化问题，MOCS有待进一步的研究和完善。

Wang等[25]提出了改进的多目标布谷鸟搜索算法（IMOCS），并用于板翅式换热器（PFHEs）的多目标优化设计。首先，在原始的MOCS中嵌入一个非均匀变异算子，以在局部搜索和全局寻优之间建立完美的平衡；然后，采用差分进化的突变，交叉和选择算子来增强种群之间的相互协作和信息交流，以提高收敛速度。实验证明，IMOCS能够获更高精度，更低不可逆性和更少迭代的最优解。

Zhang等[26]提出了混合多目标CS（HMOCS）算法来解决多目标优化问题（MOPs）。HMOCS采用非支配排序来产生帕累托前沿，并且采用动态局部搜索策略来增强局部搜索能力。在复杂的基准测试实例上，HMOCS的收敛性优于所有对比算法，但是在某些基准测试实例上，其收敛性没有NSGA-II好。

其他CS算法变体的改进思路、优缺点及应用场景如表2所示。

4.6 CS算法与其他算法的混合

如表3所示，与CS算法进行混合的算法主要有：GA、差分进化算法（DE）、和声搜索算法（HS）、PSO、ABC等。

Kanagaraj等人[38]将遗传算子嵌入到CS算法中以平衡局部搜索和全局寻优，提出了CS-GA算法。利用该算法对具有多个非线性约束的四个混合整数可靠性问题进行求解，结果表明，CS-GA算法具有更快的收敛速度，更高的求解精度。Abdel-Baset等人[39]将CS和GA进行不同的组合，提出了CS-GA和GA-CA两种算法。基于十五个基准函数证明，CS-GA和GA-CS算法比其他算法更准确、可靠和有效地找到全局最优解。

表2 其他CS算法变体的改进思路、优缺点和应用

表3 CS算法与其他算法的混合

Wang等[40]将CS与DE进行结合，提出了一种新的混合启发式DE/CS算法，对无人机路径规划问题进行求解。结果表明，DE/CS在无人机路径规划中比其他模型更有效和可行。

Sheikholeslami等[41]将和声搜索（HS）算法结合到CS算法中，提高CS算法的效率和全局收敛性，提出了CSHS算法。利用CSHS对配水系统设计问题进行优化，结果表明，CSHS算法的寻优能力和计算效率优于对比算法。

Bouyer等[42]将K-调和均值（KHM）聚类算法与改进的布谷鸟搜索（ICS）算法和粒子群优化（PSO）算法相结合提出了一种新的聚类算法，在ICS算法中，使用一个新的方程来计算半径，使其快速收敛到全局最优，此外使用MPSO来帮助ICS避免陷入局部最优。基准数据集的实验表明，所提出的算法可以获得更高质量和稳定的聚类结果。但是，在大型数据集中，算法的运行时间较长。

Zhou和Yao[43]将CS算法与ABC算法进行结合，用于云制造中的服务组合和优化选择。混合算法使用Pareto优势来指导蜂群的搜索，并维护在外部档案中找到的非支配解决方案；利用CS算法在蜜蜂搜索过程中保持种群多样性，以在帕累托前沿实现良好的解决方案的分配；此外，利用综合学习策略来平衡局部搜索和全局寻优。实验证明，所提出算法的求解质量远高于对比算法。

5 CS算法的应用

5.1 图像、信号处理

在图像处理方面，朱浩亮等[44]将改进的CS算法（MCS）用于图像分割，利用MCS算法对主动轮廓模型的能量最小化控制点进行搜索，通过实例进行测试，结果表明，MCS算法可以提高图像的分割精度，加快图像分割的速度，而且对噪声不敏感，图像分割效果优于对比方法。

在信号处理方面，Garg等[45]提出了基于CS算法的最优掩模生成方法，用于噪声抑制和语音信号增强。使用振幅幅度谱图（AMS）执行特征提取，并且进行信号分类以生成布谷鸟搜索算法的初始种群。通过各种数据集进行测试并与其他方法进行比较，实验证明，该方法大大提高了语音信号的清晰度。

5.2 负荷经济调度与电力系统

Afzalan等[46]采用改进的CS算法求解了发电机约束条件下的经济负荷调度问题。受差分变异算子的启发，新的变异方案被纳入标准CS算法，使CS算法避免陷入局部最优，从而增强算法的全局搜索能力。在含有不同热单元的电力系统下进行测试，结果表明改进的CS算法不仅可以获得更好的解决方案，而且收敛速度和计算效率均优于对比算法。

Elazim等[47]将CS算法用于多机电力系统中的最优电力系统稳定器（PSSs）参数的优化设计，并且在不同的操作条件和干扰下，将基于CS的PSSs的性能与基于GA和传统的PSSs进行了比较。仿真结果表明，基于CS的PSSs在不同的负载条件和扰动下，具有良好的鲁棒性。此外，通过时域分析，特征值和性能指标证明CS算法的有效性。

5.3 组合优化

Nguyen等[48]利用改进的CS算法求解水火电短期联合调度问题，通过满足功率平衡约束，水可用性和发电机运行限制的阀点负载效应来最小化热发电机的总成本。在具有不同燃料费用函数的三个水火电力系统上进行测试，并与其他算法进行比较，结果表明，提出的算法能够获得最小的总成本，且具有更快的计算时间。

5.4 医学应用

Liu等[49]将CS算法应用于临床疾病诊断中。采用CS算法优化支持向量机（SVM）的参数以寻找更好的初始参数，并用PSO算法对SVM进行训练，得到SVM的最佳参数，提出了CS-PSO-SVM模型。在UCI机器学习库的心脏病数据集和乳腺癌数据集上进行测试，结果表明，CS-PSO-SVM模型能够获得精确度更高的结果。

5.5 数据挖掘

Palanisamy等[50]提出步长-布谷鸟算法（Stepsize-Cuckoo Search，SCS）用于对垃圾邮件进行分类，首先利用SCS算法识别优化特征集，然后使用支持向量机完成垃圾邮件分类。实验证明，提出的方法获得了准确性更高的分类结果。Pandey等[51]将CS算法与K-means进行结合并应用于twitter情感分析问题。通过从K-means获得的解来修改CS的随机初始化过程，可以加快CS算法的收敛速度，增强算法的全局寻优能力。在四个Twitter数据集上进行测试，得到准确性高于对比算法的结果。

5.6 设计优化

Zhu等[52]提出了一种基于膜通信机制的CS算法（mCS）来优化径向基函数神经网络（RBF-NN）参数，采用膜通信机制来维持种群多样性，并采用混沌局部搜索策略来提高搜索精度。基于基准函数的测试表明，mCS可以获得更精确的解，并具有更高的收敛速度，基于mCS的RBF-NN模型具有更高的精度。

5.7 其他应用

Abed等[53]使用CS算法对伊拉克交通标志进行分类，在伊拉克原始交通标志图像上进行实验，结果表明，CS算法可以成功检测和识别伊拉克使用的所有类型的交通标志，获得了高达98%的系统识别率，并且其处理时间低至0.3 s。

其他CS算法在不同领域的应用及应用特点、效果如表4所示。

6 结束语

目前，CS算法已经被广泛应用于求解各类优化问题。但是，CS算法也存在收敛速度慢和求解精度低等缺点，限制了其应用范围和优化能力，尤其是动态优化问题的应用，迫切需要进一步研究和改进。针对CS算法在理论研究、算法改进以及实际应用方面仍有很多工作需要做。

（1）理论研究：目前的研究多数是围绕着CS算法的改进及应用，对CS算法的理论研究相对较少，对算法内部机理没有深度的研究成果，未来需要进一步完善CS算法的理论研究。

（2）融合其他算法：已经提出了CS算法与多种算法的混合，继续将其他智能技术与CS算法的有效结合，从而提高CS算法的性能，更好地平衡算法的局部搜索与全局寻优的能力仍然是进一步研究的方向。为提高CS算法的性能，还可以继续在CS算法的种群初始化、莱维飞行机制、控制参数等方面进行研究，以平衡局部搜索和全局寻优两个过程，保证种算法的群多样性，提高收敛速度。

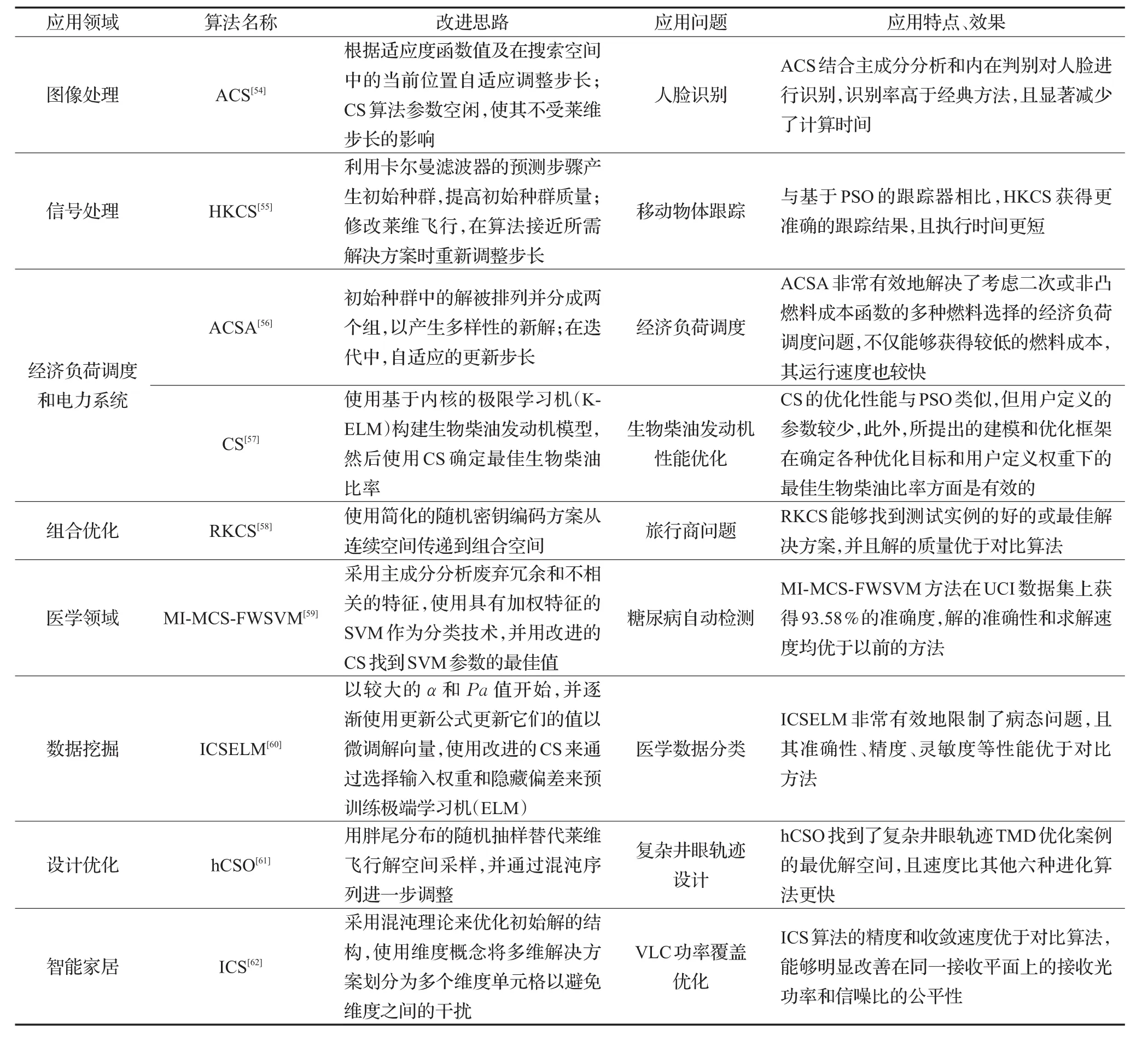
表4 其他CS算法在不同领域的应用及应用特点、效果

（3）尽管CS算法已经被应用于图像处理、生物医学、深度学习以及大规模优化等问题，但是在这些领域应用的深入研究仍然很薄弱，如何结合领域知识来提高算法的搜索性能及种群的多样性是未来的研究方向。