结构图正则低秩子空间聚类
刘 婕,马 帅
西安电子科技大学 数学与统计学院,西安 710126
1 引言
当今社会,处于一个数据爆炸的时代,充分有效地利用这些数据成为人们的必然要求。由于大多数的数据都是高维的,这给数据分析带来了不少困难。子空间聚类[1]往往是处理这类数据强有力的工具,同时可以有效地揭示高维数据的低维结构。目前,子空间聚类的方法有很多,大致可以分为四类:迭代方法[2-3]、统计方法[4-5]、代数方法[6],以及基于谱聚类的方法。在子空间聚类的诸多方法中,基于谱聚类的方法最受欢迎,例如:稀疏子空间聚类(SSC)[7]、低秩表示(LRR)[8]、最小二乘回归(LSR)[9]、光滑表示(SMR)[10],以及相关自适应子空间聚类(CASS)[11]。这些方法在原理上可以分为两步,第一步利用数据的自表示来学习相似度矩阵,第二步利用谱聚类算法得到最终的聚类结果。虽然基于谱聚类的方法取得了较好的聚类结果,但是却没有充分利用数据相似度与分割之间的依赖关系。
最近,Li和Vidal等人提出的结构稀疏子空间聚类(SSSC)[12]将上述两步结合成一步,充分利用了数据相似度与分割之间的依赖事实,用数据类别标签引导数据之间的相似度,同时利用数据相似度来引导分割。SSSC模型是SSC模型的延伸,而SSC模型单独寻找每个数据的稀疏表示,缺乏对表示系数全局结构的约束,忽略了数据间的联系和全局特征,不能很好地捕获数据的内在几何结构和全局结构。而且当多个数据与某个数据高度相关时,SSSC只会随机地选取一个数据,不能保证相似度矩阵的连接性问题。张和王[13]等人发现SSSC不能保证同类数据相似度的一致性,在SSSC的基础上增加了子空间结构低秩正则项,确保同类数据相似度矩阵的一致性,但却不能捕获数据的全局结构。Zhang和Li[14]等人受到SSSC模型的启发,在低秩表示的基础上,提出了联合学习相似度矩阵和聚类结果的统一框架,虽然该方法捕获了数据的全局结构,却忽略了数据相似度矩阵的连接性。上述方法虽然取得了较好的聚类结果,但它们都是建立在SSSC模型基础上,都存在SSSC模型存在的问题。
为了解决上述问题,同时获得一个学习相似度矩阵与聚类结果的联合优化模型,本文引入了表示系数矩阵的子空间结构范数,增加了低秩表示来揭示高维数据的全局结构。进一步,为了使相似度矩阵具有连接性,还定义了分组效应来捕获数据的内部几何结构,提出了结构化图正则低秩子空间聚类模型(SGRLRSC)。实验表明,在常用的数据集上,提出的方法优于其他先进的子空间聚类算法。
2 结构图正则低秩子空间聚类
2.1 相关工作
在基于谱聚类的方法中,假设每一个样本点都可以用来自同一个子空间的样本点线性表示,即X=XZ,其中Z为表示系数矩阵,当有噪声时,表示为X=XZ+E,其中E为噪声。通常基于谱聚类的方法统一可以写为以下形式:


2.2 SGRLRSC模型
本文在子空间结构范数上,增加了低秩表示,在集群内部定义了分组效应作为正则项,给出了一个新的统一优化模型,称为结构图正则低秩子空间聚类。
首先,为了能够充分利用数据相似度与分割的依赖事实,获得一个联合学习相似度矩阵与聚类结果的统一框架,本文通过最小化‖Z‖Q来惩罚表示系数矩阵与分割矩阵的不一致性。‖Z‖Q有效地结合了数据相似度矩阵与聚类结果,在迭代过程中,使得表示系数矩阵Z与分割矩阵Q变得一致。
其次,好的相似度矩阵会使得聚类结果更加鲁棒。对于相似度矩阵的连接性来说,希望模型能够自动地把相关性高的数据聚集在一起,即,同一子空间的数据点之间的连接性应该为1,不同空间的数据点之间的连接性应该为0。为此,本文定义了分组效应:

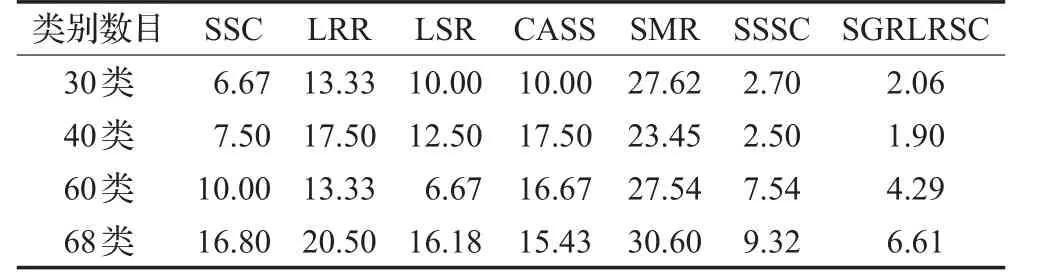
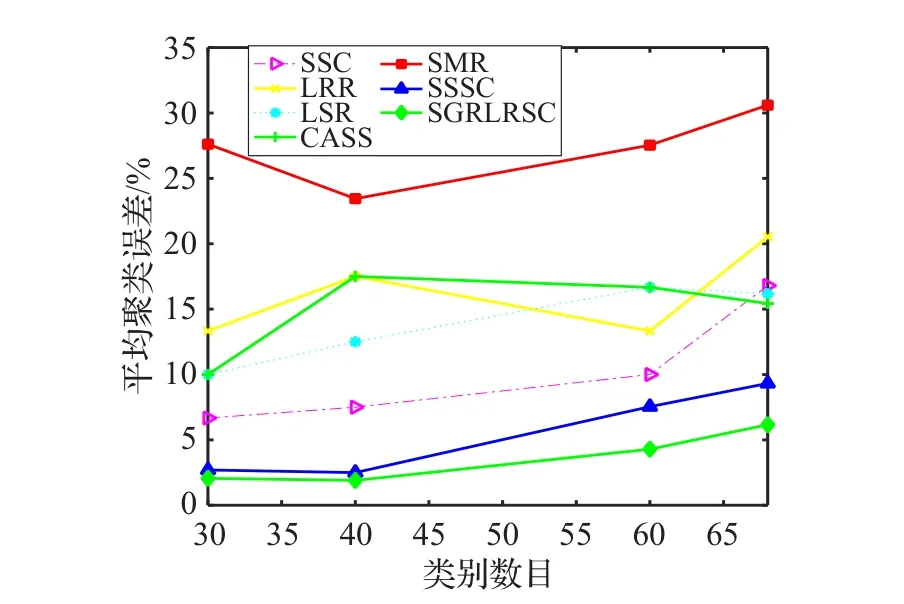
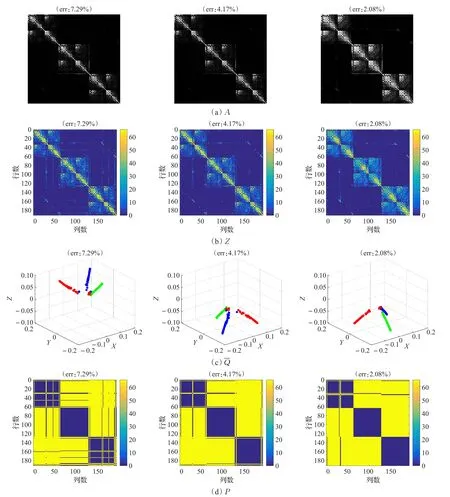
由定义可知,最大化cos 其中wij用来度量数据点xi与数据点xj的空间距离,如果,那么上式可等价于: 最后,SSSC模型中l0-范数单独寻找每个数据的稀疏表示,缺乏对表示系数的全局约束,由于低秩表示能从全局对子空间表示进行处理,因此本文对所有数据进行了低秩表示,来捕获数据的全局结构。综上所述,本文提出的模型为: 其中 λ,β,γ>0为权衡参数,Ω={Q∈{0,1}N×k:Q1=1,rank(Q)=k}是分割矩阵的空间。上述模型称为结构图正则低秩子空间聚类,简称(SGRLRSC)。 当‖‖zi2=1(∀i=1,2,…,N),那么 等价于 因此模型(5)等价于: 一方面,表示系数矩阵不但是块对角的,可以捕获数据的全局结构,迫使不相关的数据之间尽量有较少的联系,而且具有分组效应,能够捕获数据的内部几何结构,迫使高度相关的数据集聚为一类;另一方面,在迭代过程中,表示系数矩阵Z与分割矩阵Q相互平衡。初始化P=0后,对表示系数矩阵进行求解,然后利用谱聚类得到相应的分割矩阵,得到分割矩阵后在修正表示系数矩阵,如此循环下去,表示系数矩阵与分割矩阵变得更加一致,以此来得到更好的聚类结果。 模型(8)不是凸优化问题,不能直接进行求解,为了得到最优解,采用交替迭代最优化的方法求解模型。将上述问题分解为关于Q和Z的子问题,求取最优解: (1)给定Q,本文使用带自适应惩罚的线性化ADM方法(LADMAP)[16]来得到 Z 。 (2)给定Z,可以利用谱聚类得到Q。 线性交替乘子方法(LADMM)被广泛地应用于子空间聚类算法的求解问题上,在SGRLRSC模型求解时,首先固定分割矩阵Q可以利用LADMM求解表示系数Z,得到表示系数后,再更正Q。在求解表示系数矩阵Z时,由于LADMM自身的特点(矩阵与矩阵乘法以及矩阵求逆,该方法会受到计算复杂性的影响),当遇到的数据库比较大时,得到Z的最优解比较慢,那么更新Q的速度也会变慢,这样会使得最终的运算效率下降。因此采用LADMAP进行求解,LADMAP方法与LADMM方法求解模型的思想是一致的,都是通过固定其他变量求解另一个变量。但是LADMAP方法不需要引入辅助变量和逆矩阵,从而减轻了矩阵与矩阵之间的运算。在参考文献[16]中,作者在实验中已经证明了LADMAP方法的运算效率比LADMM方法运算效率高。为了证明使用LADMAP方法求解在本文中可以提高运算效率,在实验部分,在相同的条件下对比了利用LADMAP方法求解模型和利用LADMM方法求解模型在实验数据集的运算时间,LADMAP方法可以缩短运算时间,提高运算效率。 (1)表示系数矩阵Z的求解 给定Q,式(8)等价于: 那么上述问题可以由LADMAP进行求解,式(9)的拉格朗日函数为: 其中 Y1,Y2,Y3是拉格朗日乘子,μ>0是参数。 更新Z,固定C,J,E,Y1,Y2,Y3: 其中S(⋅)为软阈值算子。更新J,固定Z,C,E: 由上式可知J有解析解: 更新E,固定Z,J,C: 由上式可知E有解析解: 更新拉格朗日乘子Y1,Y2,Y3。采用梯度下降的方法,即: 便于直观的表述,算法1总结了LADMAP求解子问题Z的步骤。 算法1(LADMAP) 输入:X,P0,λ,β,γ 输出:Z 初始条件:Z=J=C=0,Y1=Y2=Y3=0,μ0=0.1,μmax=106,ρ=1.1,ε1=10-6, 循环执行以下操作: 1.用式(11)更新 Z ; 2.用式(12)更新C ; 3.用式(14)更新 J; 4.用式(16)更新 E ; 5.用式(17)更新Y1,Y2,Y3; (2)分割矩阵Q的求解 在给定Z时,问题式(8)变为: 又因为: 因此上式变为: 由于式(21)非凸,因此松弛为: 最后利用谱聚类对上述问题进行求解。 便于更直观显示模型SGRLRSC的求解过程。算法2总结了模型求解的整个过程。子问题(1)是凸优化问题,求解步骤是特征选择的过程,把表示系数Z作为特征向量来进行聚类。子问题(2)是凸松弛问题,求解步骤是谱聚类的过程。虽然上述两个子问题在理论上不能保证收敛,但是在实验中,选取一定参数,算法收敛。 算法2(SGRLRSC模型求解) 输入:X,K,λ,β,γ 输出:Q 初始条件:P0=0 循环执行以下操作: 1.当给定Q时,通过算法1求解问题式(9)得到Z; 2.给定Z时,通过谱聚类求解问题式(18)得到Q; 本文在常用的数据集CMU-PIE数据集[17],COIL20数据集[18]以及MINIST数据集[19]来验证SGRLRSC的聚类效果,并且与SSC、LRR、LSR、CASS、SMR以及SSSC方法进行比较,图1给出了实验数据集的样本图,最后,以错误率error=Nerror/Ntotal来评判上述所有方法的聚类性能。 图1 实验样本图 在实验中,为了公平,上述所有方法的参数都选取能使聚类结果最好的那个值,并且每个数据库都进行20次实验,结果取其平均值。SGRLRSC中有三个参数,λ、β、γ。在参数调整过程中,首先选择一个大的取值范围,手动地调整三个参数多次进行实验,使得聚类精度取得一个较好的结果,记下参数取值范围,然后缩小范围,通过固定其他参数的方式调整一个单独参数,使得聚类效果达到最好,取对应的参数值,以此类推,得到全部最优的值。以CMU-PIE数据集的前30类为例,在参数调整过程中,发现当β=15,SGRLRSC会取得较好的聚类结果,固定 β ,当 λ∈[0.1,0.5],γ∈[10,20],聚类误差相对较小,在实验中,不断地调整参数,使其取得最好的聚类结果。图2显示了在CMU-PIE数据集的前30类上聚类误差随参数λ和参数γ的变化图。从图像上可以看出,当λ=0.2,γ=15时,CMU-PIE数据集聚类精度最高。 图2 在CMU-PIE数据集的前30类上聚类误差随参数λ和参数γ的变化图 该数据集包含13个不同的姿势,403个不同的照明条件和四种不同表情的41 368张68个人的人脸图像,每张图像像素大小为32×32。图1中的(a)给出了样本图。在实验中,为了节省空间,仅选取每个人的21张图片,构建了30、40、60和68类的四个子空间。大量测试实验表明,当λ=0.2,β=15,γ=15时,聚类精度最高。表1显示了各种方法在CMU-PIE数据集的聚类结果,对于不同类,选择一样的参数。从表中可以看出,SGRLRSC方法始终优于其他方法。便于更清楚地对比各个方法的聚类性能,图3给出了各种方法在30、40、60和68类的四个子空间上的聚类错误率曲线图,从曲线图上可以看出随着类别数目增多,SGRLRSC方法的聚类性能慢慢退化。 表1 在CMU-PIE数据集上的聚类错误率 % 图3 聚类错误率随CMU-PIE数据集数目增多的变化图 为了进一步说明SGRLRSC模型的作用,图4显示了在不同错误率下,相似度矩阵A,自表示矩阵Z,相似度矩阵A的最小的三个特征值所对应的特征向量(Qˉ)以及连接矩阵P。为了可视化,都取其绝对值并且乘以800。由图可知,随着错误率变低,相似度矩阵A越来越接近块对角矩阵,表示矩阵Z与分割矩阵Q也变得越来越一致。 图4 SGRLRSC方法中矩阵A、Z、向量及矩阵P在不同错误率下的可视化图 COIL20数据集是由20个物体在不同角度下构成的1 440张灰度图像,图1(b)给出了实验样本图。每个物体只选取前50张图片作为样本,在实验中,将每张图片像素32×32向量化后,利用主成分分析(PCA)[20]降维成60维。大量实验结果表明,当 λ=0.5,β=15,γ=0.1,SGRLRSC的聚类效果最好,表2给出了SGRLRSC方法在COIL20数据集的聚类精度,由表2可知SGRLRSC方法的聚类性最好。 MINIST数据集是一个在子空间聚类中经常会用到的包含数字0~9的10类手写字体数据集。每个图片的分辨率大小为28×28,对应于784维向量。图1(c)给出了实验样本。在实验中选取50个样本作为数据集,并且将每个样本投影成60维。在实验中,取λ=0.05,β=90,γ=1.9,SGRLRSC的聚类效果最好。实验结果如表3,由表3可知SGRLRSC方法提高了聚类精度,并优于其他算法。 表2 COIL20数据集的聚类误差率 % 表3 MINIST数据集的聚类误差率 % 表4 不同求解算法在各个数据库的运行时间 s 最后为了证明使用LADMAP方法求解模型在本文中可以提高运算效率,表4给出了不同求解算法在各个数据库的运行时间,由表4可知使用LAD MAP方法求解可以提高运算效率。 本文在子空间结构范数的基础上,引入分组效应和低秩表示,给出了一种新的子空间聚类模型,其优点是该模型不但利用了学习相似度和聚类结果的统一,而且还可以同时捕获数据的全局结构与内在几何结构。自适应惩罚的线性化交替法也被引入来寻找模型的最优解。大量实验表明本文提出的方法优于其他子空间聚类算法。





3 模型求解


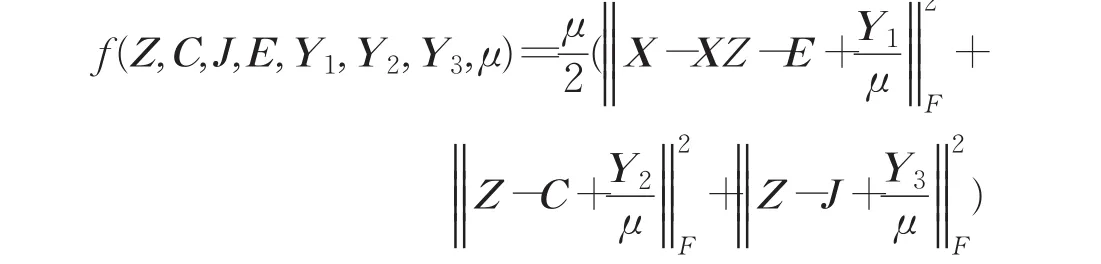

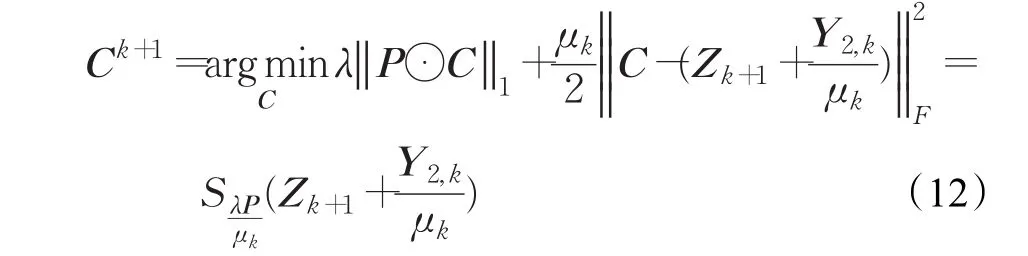








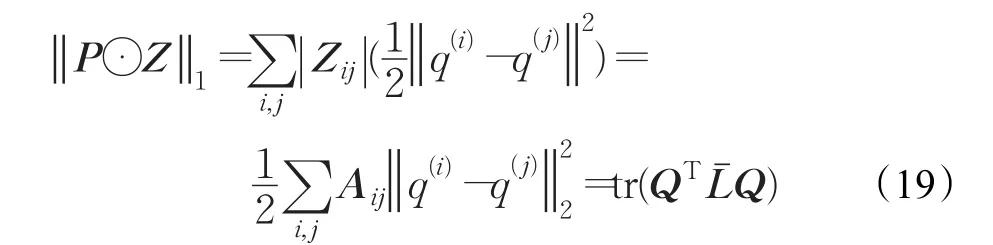

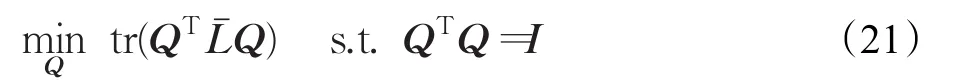
4 数值实验

4.1 CMU-PIE数据集

4.2 COIL20数据集
4.3 MINIST数据集



5 结束语

