知识有形，思想无形——从一道平行线“折线形”习题谈数学思想

黑龙江省五常市第一中学校 曹雨杰

随着新课程改革的不断推进，中高考制度进一步深化改革，数学思想方法的地位和作用越发凸现出来。《数学课程标准（2011年版）》提到：“课程内容要反映社会的需要、数学的特点，要符合学生的认知规律。它不仅包括数学的结果，也包括数学结果的形成过程和蕴涵的数学思想方法。”本文笔者将结合一道初中数学习题的教学，谈一谈教学中数学思想的渗透。

一、截大补小，巧用转化

在七年级数学第五章《相交线与平行线》的一节习题课上，遇到了这样一道习题：

已知：如图1，AB∥CD。

求证：∠ABE +∠EDC =∠BED。

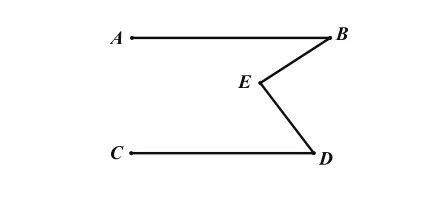
图1

本题的考点是：平行线的性质。由于之前的习题大多是“三线八角”式的基本图形训练，这道“折线形”的习题无疑让学生不知如何下手，所以，引导学生将其转化成我们熟知的平行线基本图形，便是解决这道题的关键点。经过老师的引导，学生容易想到过转折处的E点作EF∥AB，进而将原图拆分成如图2的形状，这样，证明两个角和等于第三个角的问题，就转化成了两组平行线基本图形中内错角的问题了，将未知转化为已知，问题迎刃而解。

图2

“转化”思想在数学中的应用，不仅可以开拓学生的思路，更能提高学生的学习兴趣，使学生在轻松愉快中享受数学学习的快乐。接下来，我们可以继续引导学生思考：既然我们可以将大角分成两个小角，再证明它们与各自的内错角相等，那么，我们可不可以将两个小角合在一起，证明得到的两角和与大角相等呢？于是便有了如图3的证明方法。（过点D作DG∥BE，交AB延长线于点G）

图3

“截大”与“补小”殊途同归。“分”与“合”之中，不动声色地渗透了数学中较为常用的转化思想。通过训练，让学生养成多角度考虑问题的习惯，形成科学的思维习惯，优化学生的思维品质。

二、逆向发散，变中不变

如果我们将本题的题设与结论交换位置，那么，一道平行线的性质题就会转变成平行线的判定问题。即：

已知：如图4，∠ABE +∠EDC =∠BED。

求证：AB∥CD。

图4

既然图形没有改变，仿照原题的证明方式，学生便可以很快找到解决问题的方法。其实好多老师在注重转化思想的同时，却忽视了“变中有不变”的数学思想，我们可以从一道习题入手，给出多种解题路径，引导学生通过将未知转化成已知解决新的问题，从中培养和发展学生的数学思维能力。

因势利导，我们可以将点E的位置适当改变，形成一道新的平行线性质题：

已知：如图5，AB∥CD。

求证：∠ABE+∠EDC+∠BED=360°。

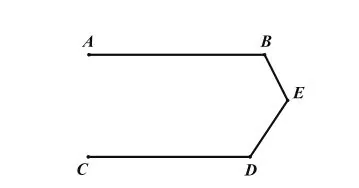
图5

虽然图形变了，结论也变了，但学生依旧能够很快根据原题的思想和方法，过转折点E作AB的平行线，轻松解决问题，也许，这也正是数学的魅力所在。莫斯科大学教授C.A.雅洁卡娅演讲时曾提出：“解题就是把要解题转化为已经解过的题。”透过有形的文字和图形，挖掘隐藏在背后的无形的数学思想，则可以让学生从整体上、本质上理解数学，科学灵活地使用数学方法解决问题。

三、举一反三，联想类比

《论语·述而》中有：“举一隅不以三隅反,则不复也。”如果我们继续将原题中点E的位置进行改变，形成图6的样子，已知不变，并将结论开放，这样就可以进一步拓展学生的思维能力，帮助学生学习新技能,达到举一反三、触类旁通的目的。

图6

已知：如图6，AB∥CD，连接BE，DE。

探究：∠ABE、∠EDC、∠BED 有何关系？

通过类比之前的习题，过转折点E作AB的平行线，学生能够很快得出结论：∠ABE-∠EDC=∠BED。由此知彼，由旧知新，我们只要发现此题与原题之间的联系，加以认真思考,就能够在新的图形中模仿学过的数学方法解决问题。

既然可以改变点E的位置，那么，点E都可以在哪里呢？每个相应位置的结论又是怎么样的呢？学到这里，学生不免有这样的好奇心理了。言有尽而意无穷，难道点E的位置有无限多吗？答案当然是否定的。

四、一网打尽，分类讨论

要想知道点E到底有多少位置，这里就不得不使用分类讨论了。所谓分类讨论，就是分别归类再进行讨论的意思，为了寻找它们各自的共同点及内在的规律性，首先就要找到区别于不同位置的分类标准。深入思考以后我们不难发现，平行线AB、CD和截线BD将平面分成了六个部分（如图7），如果不考虑点E落到这三条线上，则点E的位置共用六处。正确选择分类的标准，进行合理的分类后，就可以逐类讨论解决，所用方法类比之前的，学生可以很快给出各个位置上的结论。

图7

五、授人以渔，建立模型

为了进一步激发学生的学习兴趣，根据“学数学、做数学、用数学”的理念，鼓励学生探究，培养他们的创新精神，除了改变点E的位置外，还可以改变折线的条数和方向，如图8、图9。仿照原题建立模型，由哪转折，在哪作线，即可解决类似问题。

图8

图9

总之，数学的世界是丰富多彩的，我们要学会用数学的眼光看世界。一节课不能让你通晓所有的数学奥秘，但却可以启发你探究数学的思维。与“有形”的数学知识相比，那些“一切已学过的东西都忘掉时所剩下的东西”就是“无形”的数学思想。作为一名中学数学教师，只有领悟并掌握数学的基本思想,才能更加准确地理解教材，有效组织教学，进而让学生在学习中体悟到数学思想，使学生的思维水平得到提高。