关于四色猜想的几何证明和其在多维空间推论的构造及可能性探讨

中国人民大学附属中学 滕笑非

四色猜想，又称四色问题，是世界三大数学猜想之一，最先是由一位叫弗朗西斯·古德里的英国大学生提出的。四色猜想的具体内容是：“任何一张地图使用四种颜色就能使具有共同边界的国家着上不同的颜色。”也就是说在不引起混淆的情况下，一张地图只需要四种颜色来标记。

用数学语言表示即：“将平面任意地细分为不重叠的区域，每一个区域总可以用1、2、3、4这四个数字之一来标记而不会使相邻的两个区域得到相同的数字。”这里所指的相邻区域是指有一整段边界是公共的。如果两个区域只相交于一点或有限多点就不叫相邻，因为用同种颜色给它们着色不会引起混淆。

作为世界三大数学猜想之一，四色猜想的证明一直是一个引人入胜的题目。自从它在1852年被提出，无数数学家都尝试证明四色猜想，但都无功而返。直到1976年6月，通过电子计算机1200小时中做的100亿个判断，证明了确实没有任何一张地图需要用5种颜色，四色猜想终于被证明。但是计算机证明终究不是理论证明，虽然遍历了100亿个判例全部通过，但这并不能说明不存在极端反例。在此，本文给出四色猜想的平面几何证明方法。

一、四色猜想的几何证明

首先，建立数学模型。之所以需要四种颜色才能区分，是因为存在四个两两相交的区域，这样我们必须让任何一个区域的颜色都与另三个不同。如果对于任意四个两两相交的区域A、B、C、D，存在第五个区域E，使E与A、B、C、D均相交，则E需要用第五种颜色染色。换言之，若要证明四色猜想，只需证明不存在五个两两相交的平面图形即可。

因为在四色猜想中，区域的形状并不重要，重要的是区域之间的相交关系，所以我们采用了理想模型简化问题。将任何平面几何图形理想化为圆，将区域之间的相交表示为两圆相切，则任意两个有公共边的凸多边形可以表示为圆A外切圆B；任意两个有公共边的凹多边形A、B也可以表示成圆A外切圆B（如图1）；任意凸多边形A和凹多边形B有公共边可以表示为圆A内切圆B（如图2）。另外，不存在圆C同时内切圆A、B且切点均为O的情况，因为虽然这样圆A、B、C满足两两相切，但在非理想情况下，A、C区域并不存在公共边（如图3）。我将这样的圆C定义为二次内切圆，易得这样的理想模型中不应存在二次内切圆。这样我们就通过理想化模型表示了平面图形之间的位置关系，我们需要证明的命题也转化为“在没有二次内切圆的情况下，不存在五个两两相切的圆”。

图1

图2

图3

由于对于任意给定闭合区域和给定个数的给定圆，若在该区域内存在一圆使其与所有已知圆相切，则该圆一定是固定唯一的；对于任意给定开放区域和给定个数的给定圆，若在该区域内存在一圆使其与所有已知圆相切，则该切点一定是固定唯一的。所以我们可以用BFS（广度优先搜索）算法，遍历所有区域，判断该区域内能否存在一个满足与所有已知圆相切，直到所有可能性都不能再添加进去的新的圆后结束遍历，即可判断最多能存在几个两两相切的圆。

BFS遍历过程如图4所示：

图4

综上，在不存在二次内切圆的情况下，不存在五个两两相切的圆，即平面内不存在五个两两之间存在公共边的图形，四色猜想得证。

二、四色猜想在其他已知维度内的推广

若要进行这个推广，首先要严格定义n维图形（n∈N+）相交。不难发现，在一维空间中，相交的定义为共端点（点认为是零维面）；在二维空间中，相交的定义不再使用存在公共点而是改为公共边（边认为是一维面）；三维空间中，相交的定义则变成至少有一部分面积接触，换言之即是存在公共面。也就是说，对于n为空间（n∈N+）中的n维图形，相交的判定应为存在公共的（n-1）维面。

在这个定义下，我们发现：

一维空间中两两相交的一维图形最多只存在两个，即只需要2种颜色即可染色。

二维空间中两两相交的二维图形最多只存在四个，即只需要4种颜色即可染色。

三维空间中两两相交的三维图形最多只存在八个，即只需要8种颜色即可染色。

以上均通过与四色猜想几何证明相似的理想模型假设法证明。

三、关于四色猜想在多维空间推论的猜想

根据四色猜想在已知维度内推广的结论，我猜想该推广在n维空间（n∈N+）中均适用，且满足“n维空间中两两共（n-1）维面的n维图形最多只存在2n个，即只需要2n种颜色即可染色”。

四、关于四色猜想在多维空间内推论猜想的合理性讨论

多维空间不同于三维以下空间，有几何工具并且可以通过人脑直接想象。对于四维及以上空间的研究只能停留在纯代数领域，此处引入拓扑学原理进行讨论。

拓扑学是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科，它只考虑物体间的位置关系而不考虑它们的形状和大小。

在拓扑学里不讨论两个图形全等的概念，但是讨论拓扑等价的概念。比如，圆和方形、三角形的形状、大小不同，但在拓扑变换下，它们都是等价图形；足球和橄榄球，也是等价的——从拓扑学的角度看，它们的拓扑结构是完全一样的。

在拓扑学原理的前提下，我们可以将任意维度的几何图形简化为一个节点，如果两节点之间存在一条无向边则称他们是相交的，这种无向边是一种逻辑关系，即两两相交的n个图形满足：这n个节点两两之间存在一条无向边，且这些无向边没有交叉的，否则说明其中一种连通关系是建立在另一种连通关系之上而非直接相交的。

如此一来，我们将高维度难以想象和计算的问题转化为求给定维度下最多能存在多少个点，使得这些点两两连线互不相交？

为了方便表示，我们定义数列{an}，其中第i项ai表示在i维空间中，满足任意两点连线互不相交的最大点的个数。这表示i维空间中最多存在ai个两两相交的i维图形，也就是需要最多ai种颜色即可完全染色i维空间的任意连续图形。

根据我们的猜想，{ai}的通项公式为ai=2i（i∈N+）。

下面不加证明地给出在i维空间中，构造2i个点，使任意两点连线互不相交的方法：

定义：n维空间中，满足命题题意的最大数量的点组成的n维点阵成为n维时的最大点阵。

i=1时，显然a1=2。若放入第三个点，在一维空间中势必构成三点共线，使得点之间连线相互重叠。i=1时的最大点阵如图5所示。

对于任意i≥2，该i维点阵中一定存在若干个（i-1）维面，若任意（i-1）维面的点数量小于ai-1,则该（i-1）维面一定能再放入一个点，若数量大于ai-1，则该（i-1）维平面一定与命题矛盾。即当且仅当该点阵的每个（i-1）维平面都是（i-1）维时的最大点阵时，该点阵为i维的最大点阵。

i=2时的最大点阵如图6所示，a2=4。

图5

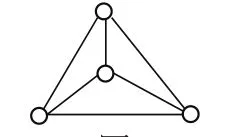
图6

图7

i＞2时，任取（i-1）维最大点阵一点，将其以第i维度的方向平移。不难想象，该操作会构造出新的（ai-1-1）个异于原最大点阵的（i-1）维面，此时的ai-1个点构成一个有ai-1个（i-1）维面的i维图形。在所得的i维图形的每个（i-1）维面上各任意选取一个面内点，则会构造出ai-1个新点，这2ai-1个点即为i维的最大点阵。由构造过程可得，对任意 i＞2，ai=2ai-1。

i=3时的最大点阵如图7所示，与猜想相符。

由于知识水平和技术手段的限制，本文只能给出上述构造方法，但无法严格证明。目前的想法是采用计算机的高维数组储存多参数变量进行高位计算来验算其可行性，但是遍历算法，验算n维构造的估算时间复杂度约O（n2·22n），以目前的技术，该时间复杂度仍然过高。希望将来可以开发更先进的针对多维空间的算法来证明本文对于四色猜想在多维空间推论的猜想。