一类平面向量问题的解题技巧

福建省武夷山第一中学 葛香珠

高考试题“源于教材，高于教材”，从教材中寻找试题的生长点，钻研教材，有利于发挥教材的教育教学功能。下面利用平面向量的共线定理，我们可以得到一个很实用的结论，限于篇幅，略举三例。

结论：已知A,B,C三点共线，O是平面内的任意一点，则存在实数x,y,使得

证明：因为 A,B,C三点共线，所以存在实数λ，使得 ，

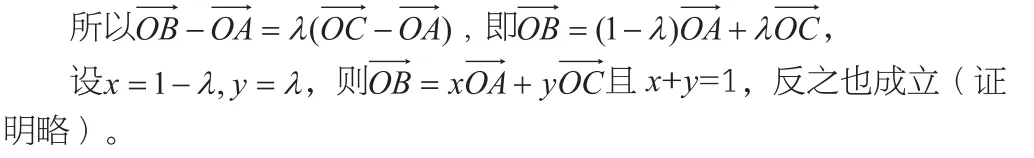
下面将从三个例子解释其应用规律。

解：由题设知A,M,Q三点共线,根据上面结论得，存在实数x,y,

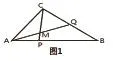
图1

例2 如图2，给定两个长度为1的平面向量 和 ，它们的夹角为120°，点C在以O为圆心的圆弧AB上移动。若其中x，y∈R，则x+y的最大值为 __________。

解：设AB与OC交于点D,

根据上面定理及结论，存在实数m，n，λ,

根据平面向量的基本定理得m+n=λx+λy=1（λ＞0），

图2

故x+y的最大值为2。

例3 （2017课标3，理12）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上。若则λ+μ的最大值为( )。

解：如图3所示，建立平面直角坐标系，

图3

设AP与BD交于点E，

根据上面定理及结论，存在实数x，y，λ，

过点P作PF∥AB交直线BD于点F，则△ABE与△PFE相似，

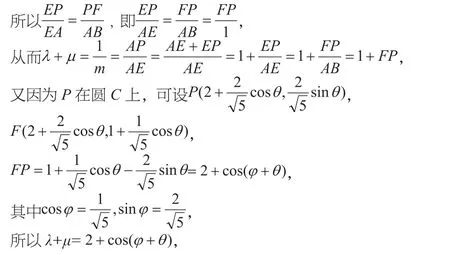
以上例题采用建立恰当的坐标系，利用函数与方程的思想方法解题，也是不错的思路，读者不妨试试。

我们可以把上面的定理和结论作为一个解题模板，用来研究形如的题型，特别注意三点共线时，x+y=1是解决这类问题的关键点和难点所在，必要时结合平面向量的坐标运算，几何知识与三角函数会加快解题速度。