数学解题中常见的心理性失误案例剖析

安徽省枞阳县钱桥中学 (246732) 吴灵梅安徽省枞阳县浮山中学 (246736) 唐录义

很多学生进行试卷分析时，都会将失分归因为两类：第一类是由于知识和能力不足而导致的，第二类是具备了解决这个问题的可能性却没有得到正确的答案.对于“第一类失误”学生往往会比较认真地对待，寻找自己需要提高的地方；而对于“第二类失误”很多学生却不以为然，往往给这类失误简单地下个结论，如粗心大意或是归结到状态不好，导致不知怎地就错了.所以他们对第二类失误并不太在意，以至于在屡次考试中不能改善，即使考试时非常小心也总会出错，然后因认为自己犯了不该犯的错误而垂首顿足，这使学生变得沮丧，严重影响到他们学习数学的态度和信念.长此以往，将会使学生学习数学的积极性受到严重挫伤.其实这种现象的背后往往隐藏着深层次的心理原因，如思维抑制，粗心大意，思维惯性，思维定势，审题习惯不好等都可能是造成这种失误的原因，我们把这类失误称之为心理性失误．

1.思维抑制，导致低级错误

在考试中由于临场过分焦虑紧张甚至出现慌张，心理压力过大以至于出现暂时性思维障碍，称为思维抑制．这种情况下，面对题目，往往大脑一片空白，不知所措，平时常用的知识和方法记不清了，想不起来了，题目也容易看错，简单的运算也会发生错误，这种情况常常出现在考试开始阶段．另外，在考试中途因某题较难而求解遇挫，也会引起情绪紧张，心里慌乱，从而干扰思维的正常运行，导致会而不对，对而不全．造成思维抑制的根本原因是情绪过于紧张，思想压力过大，心理负担过重，或者是对考试中的困难和应对策略缺乏必要的心理准备．

考点涉及：函数的图像，数形结合的数学思想.

错解呈现：当x>0时，f(x)=f(x-1)，所以当x>0时，f(x)是周期函数，周期为1.当x≤0时，则f(x)=x-[x]，这时函数也为周期函数.作出图像如图1：

图1

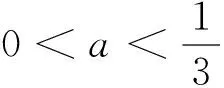
错点查找：(请仔细阅读上面的“错误呈现”，并将其中错误之处勾画出来)以上解答将合理地分析试题结构，正确地画出函数图像.但是没有注意到题意，题中要求f(x)与y=ax有三个不同的交点，而不说f(x)与y=ax至少有三个不同的交点，即只能有三个交点而不能有四个交点.

出错归因：思维抑制，导致低级错误，本题中的错解源自于对题意的误解.

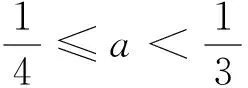
反思总结：思维抑制，导致低级错误.问题比较复杂，做题对图像的刻画较为慎重，问题的分析也比较周到.但最后犯了较为低级的错误，试题中的要求是“三个不同的交点”而不是“至少三个交点”，从而导致错解.

2.思维惯性，思维定势，思维僵化

我们在长期的工作、学习和生活中，对经常发生的事情，在思考过程中，往往会产生思维惯性，形成固定的思维模式，即思维定势.思维定势对常规思维是有利的，它可使思考者在处理同类问题的时候少走弯路.然而，思维定势也有它的弊端，特别是当我们处理一些新情况的时候，思维定势就会变成“思维枷锁”，阻碍我们用新观念、新方法、新思路去创造性地解决问题，使人失去创新和发展的源泉和动力.

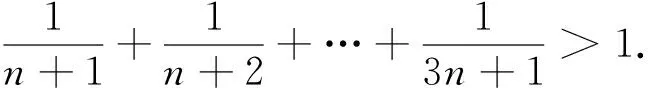
考点涉及:数学归纳法.

错解呈现:(1)当n=1时，不等式成立.

就是说当n=k+1时不等式成立.由(1)(2)知原不等式成立.

出错归因:思维惯性，思维定势，思维僵化导致出错.

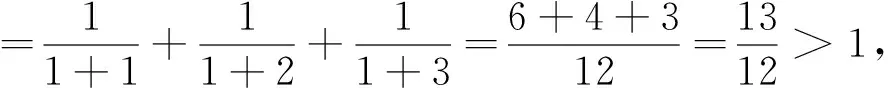
这就是说，当n=k+1时，不等式成立.

由(1)(2)知原不等式成立.

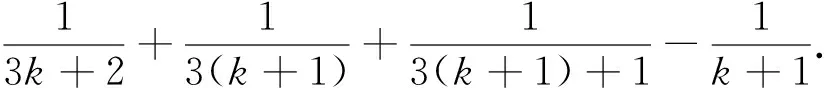
3.审题浮浅，理解肤浅

粗心大意源于不良的学习习惯，包括阅读习惯，审题习惯．阅读不专注，思考不深入，浅尝辄止，未窥及深潜，忽略隐含条件，粗心大意，看错或看漏条件，或者只考虑问题的某个方面，忽略了问题的其他方面，顾此失彼．

案例3 已知f(x)是定义在R上的奇函数，当x>0时，f(x)=x2-4x+5，求f(x)在R上的解析式.

考点涉及：函数的奇偶性及其性质应用.

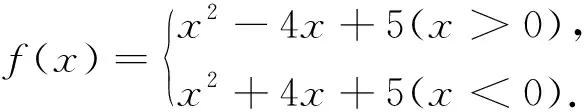
错点查找：(请仔细阅读上面的“错误呈现”，并将其中错误之处勾画出来)上述解法中，只注意到函数的奇偶性，而忽略了函数的定义域，f(x)是定义在R上的奇函数，所以必须要考虑到x=0时的情况.

出错归因：理解不透，忽略隐含条件.本题中函数f(x)在x=0时有定义，但函数在x=0时又是间断的，解题容易疏忽.

正解参考：由题意f(x)是定义在R上的奇函数，当x<0时，f(x)=-f(-x)，这时-x>0，所以

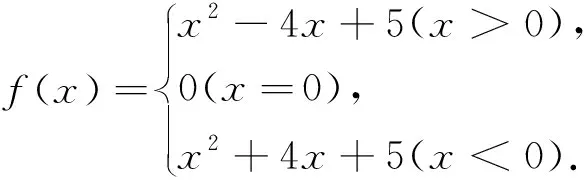
反思总结:函数奇偶性的性质①奇、偶性是函数的整体性质，对整个定义域而言；

②如果一个奇函数f(x)在x=0处有意义，则f(0)=0，对偶函数而言，对定义域中的任意x，有f(x)=f(|x|)；③奇、偶函数的定义域一定关于原点对称，如果一个函数一定不具有奇偶性，称之为非奇非偶函数；④如果函数既是奇函数又是偶函数，则叫做既奇又偶函数.例如f(x)=0；⑤任意常函数(定义域关于原点对称)均为偶函数，只有f(x)=0是既奇又偶函数；⑥奇函数在其定义域上的对称区间上具有相同的单调性，偶函数在其定义域上的对称区间上具有相反的单调性.

4.观察不仔细，认识不全面

观察,是研究数学问题的起点,其重要性不言而喻.观察数学问题的关键是细致入微，洞若观火，不放过任何细节和线索，这样才能深入全面地获取解题信息.否则，观察不仔细，粗心大意，丢三落四，认识不全面，就会导致错误.

案例4 以下四图，都是同一坐标系中三次函数及其导函数的图像，其中正确的序号是( ).

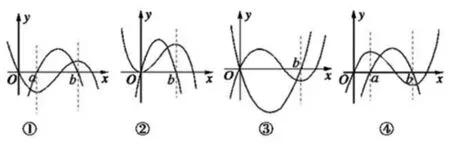
(A)①② (B)③④ (C)②③ (D)①④

考点涉及:导数与原函数的单调性的关系，函数图像.

错解呈现:在图④中，原函数在导数的零点处改变它的单调性，故④正确；在图③中刚开始时，原函数与其导函数单调性步调一致且单调性恰好相反，故③正确；本题正确的答案为B.

错点查找:(请仔细阅读上面的“错误呈现”，并将其中错误之处勾画出来)错解没有理解清楚原函数在区间上的单调性与对应的导数的关系，即函数在区间上单调递增时，导数大于零；函数在区间上单调递减时，导数小于零.

出错归因:心理性失误，观察不仔细，认识不全面，导致推理失误.本题中的错解源自对原函数与其导数的关系理解混乱.

正解参考:由图像可知，在图①，②，在每个区间上函数的单调性与导数的符号是对应的，即函数增区间的导数大于零，单调减区间的导数小于零；在图③中图像显示在区间(0,b)上导函数的值总为负值，而相应区间上的函数图像显示不单调，二者不一致，所以③不正确；图④中图像显示在区间(a,b)上导函数的值总为正值，而相应区间上的函数图像却显示为减函数，而该区间上的函数图像显示不单调，二者不一致，所以不正确；二者不一致，所以④不正确.故选A.

反思总结:判断一个函数在某个区间是否为增函数时要看导函数在该区间是否大于0，而不是看导数的单调性与原函数的单调性是否一致(单调性相同或者相反).其次我们要掌握三次函数图像的特点，三次函数的导数如果有两个不同的零点，则其图像呈“N”或者倒立的“N”；三次函数的导数如果有两个相同的零点或者没有零点，则其图像是我们熟悉的立方抛物线.

5.缺乏韧劲，知难而退

水流千里意志坚，人无韧劲半路亡.跌倒了并不意味着失败，关键在于是否能忍着疼痛，漂亮地重新站起来，只要有梦想那么你永远都不会输！人有很多时候不是败给了别人，而是输给了自己.韧者，柔而固也.固而不柔则脆，柔而不固则弱，柔而固则韧.歌德说，世上只有两条路能通往成功的目标并成就伟大的事业，那就是力量和坚韧.坚韧从来不负众望，因为它沉默的力量将随着时间的推移一天天壮大，直到所向披靡，无以抗拒.古人云：“锲而舍之，朽木不折；锲而不舍，金石可镂”．毅力也是成功之本，是一种韧劲.数学解题如果缺乏韧劲，遇到思维难度稍大一点的问题就不深入思考，遇到运算量繁冗一点的题目就望而却步，知难而退，轻言放弃，就会错失成功的机会.

考点涉及:利用导数求函数单调性，分类讨论的数学思想.

因为函数f(x)=2lnx+x2-5x在区间上为单调函数，所以

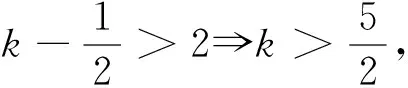
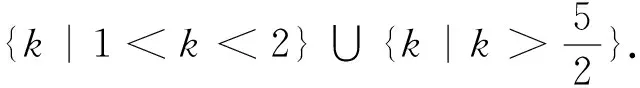
出错归因：看到复杂的结构式，遇到运算量繁冗一点的题目就望而却步，知难而退，轻言放弃，就会错失成功的机会，属心理性失误.

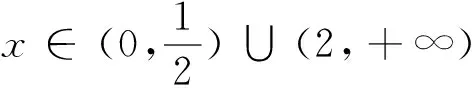
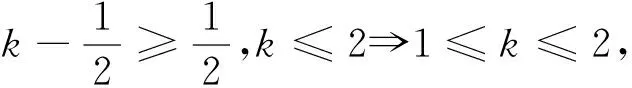
反思总结：同学们在解导数问题，特别是含有lnx类的函数单调性问题，不单要结合函数的定义域来解题，而且要关注函数在开区间端点处的取值，培养读题，审题，解题，反思的解题习惯，培养严谨的解题行为，考虑问题要全面，做到不重不漏.