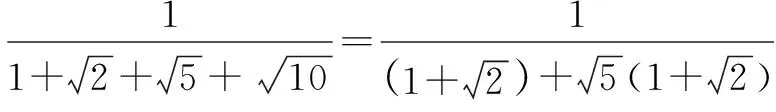例谈竞赛中含根号问题的解法
周友德
(安徽省芜湖市无为县蜀山镇黄姑小学 238361)
一、利用平方差公式:a2-b2=a+ba-b
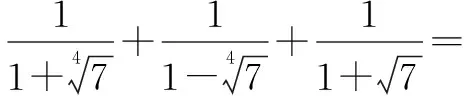

除了上述常见的分母有理化外,还有分子有理化:

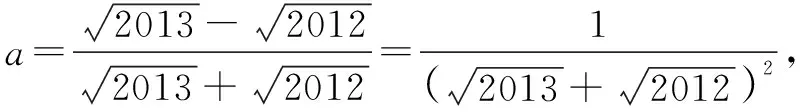

故a 同理: 故x 评析利用平方差公式,将分数分母(或分子)有理化,从而使题目得到化简,避免了繁琐的解答. 例5 (2013年北京市初二竞赛题改编)化简 ①②相加减即可得到如下公式: 评析利用完全平方公式,可以将含多个根号的数,逐步去根号,得到最终的答案,但是前提是知道根号下的数到底是什么数的平方,这才是关键.必需不断的做题,练习,总结. …… 评析合情推理是波利亚的"启发法"中的一个推理模式2.就是从已有的知识和具体的事实经验出发,通过观察、实验、类比、联想、归纳、猜想等手段在某种情境和过程中推出可能性结论的推理.要做此类题时,一定要大胆猜想,通过对前几项根号的逐步计算,通过合情推理,得出最终的结论. ⟹x3=4-3·x ⟹x3+3x-4=0 ⟹x-1x2+x+4=0 ⟹x=1 ⟹x3=12+5x ⟹x3-5x-12=0 ⟹x-3x2+3x+4=0 ⟹x=3 评析通过完全立方公式a+b3=a3+b3+3aba+b化简这类根号题,必须先令整个式子为x,然后两边三次方,从而解出实数x.但要注意两个三次根号下的数必须是对偶数才可以用此法. 综合化归,即综合前面所讲的所有方法进行化归,对学生的能力要求更高. ①+②+③得: 解可得1994=2x-12即4x2=4x+1993,故4x3-1997x-1994=x(4x+1993)-1997x-1994=4x2-4x-1994=1993-1994=-1 ⟹4x3-1997x-19942001=-12001=-1. 解可得3=a+12⟹a2-a+1=3-3a ⟹原式=a3a2-a+1+a2-a+1=a3+1a2-a+1 =a+1a2-a+12 =a+13-3a2 评析含根号的题目变化万千,但只要掌握其本质,就能一招制敌,要会举一反三.这样才能在做题时,多角度,多思维地去考虑,才能在做题中找到合适的方法. 通过以上的多种方法的化归,转化过渡,就能使问题能由繁变简,由难变易,通过多元化的解题方法能让学生更加体会到数学中的千变万化的美.学生应在不断做题中,在方法的不停的交汇中,就能达到自身水平的提高,这样才会在解题时,找到浑然天成的解题方法.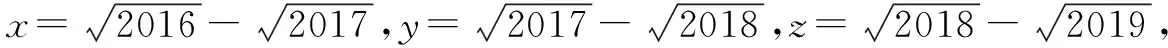

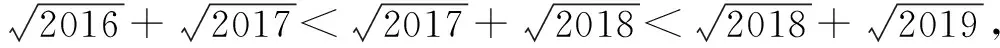
二、利用完全平方公式:a±b2=a2±2ab+b2

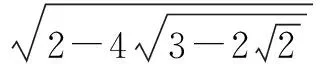
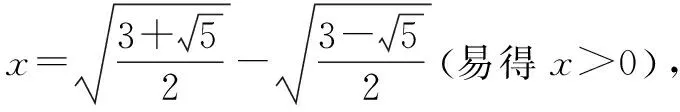

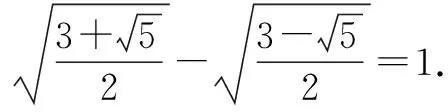

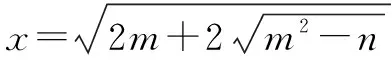
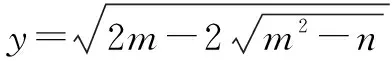
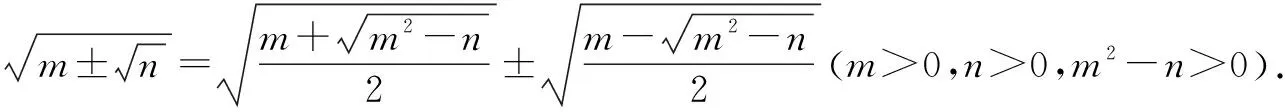
三、利用合情推理

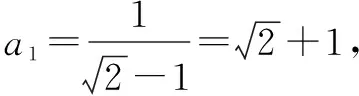

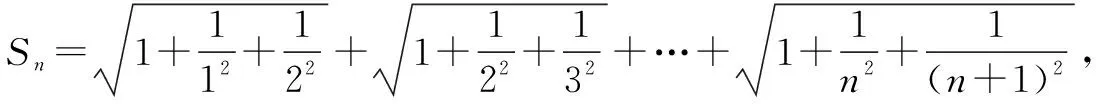

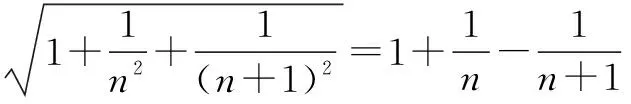
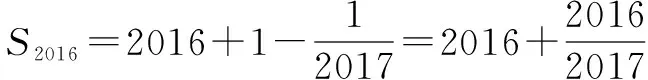

四、利用完全立方公式:a+b3=a3+b3+3aba+b

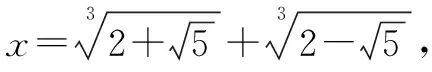
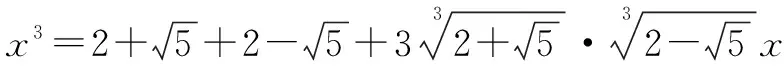
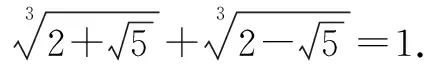



五、其他升级
1.综合化归

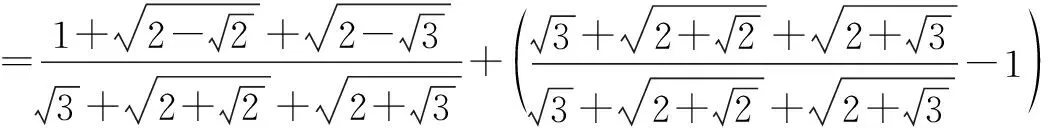
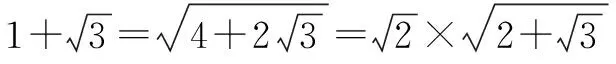

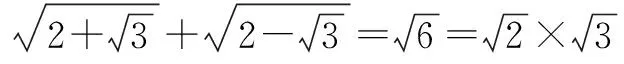

2.整体代换
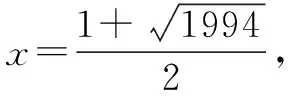
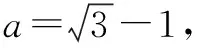
3.裂项变形


4.因式分解