对《数学必修2》的《立体几何》一章的修改建议*—谈立体几何证明题表述的规范化

广东省肇庆市高要区第一中学(526100) 程华生

在高考中,数学解答题有6个,其中必有1个是立体几何的题目,立体几何是高中数学知识的一大板块.

在日常教学中,我发现很多资料上给出的立体几何证明题的参考答案,存在很大缺陷,包括课本上给出的立体几何证明题的答案也是有待改进的,它们的共同缺点是:缺条件.

在此,我提倡立体几何证明题表述的规范化.

首先,我给出立体几何常用的10个判定定理和性质定理.

(1)线面平行的判定定理

文字语言:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行.

符号语言:a//b,a/⊂α,b⊂α⇒a//α.

3个条件推出1个结论.线线平行⇒线面平行.

作用:证明直线与平面平行的方法一(第一选择)

(2)线面平行的性质定理

文字语言:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.

符号语言:a//α,a⊂β,α∩β=b⇒a//b.

3个条件推出1个结论.线面平行⇒线线平行.

作用:一个题目有“线面平行”的条件时,由此条件可以推出“线线平行”.

(3)面面平行的判定定理

文字语言:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.

符号语言:a⊂β,b⊂β,a∩b=P,a//α,b//α⇒α//β.

5个条件推出1个结论,但是前面2个经常省略不写,“3个条件推出1个结论”即可.线面平行⇒面面平行.

作用:证明两个平面平行.

(4)面面平行的性质定理一

文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.

符号语言:α//β,α∩γ=a,β∩γ=b⇒a//b.

3个条件推出1个结论.面面平行⇒线线平行.

作用:一个题目有“面面平行”的条件时,由此条件可以推出“线线平行”

(5)面面平行的性质定理二

文字语言:如果两个平面平行,那么其中一个平面内的任意一条直线都和另一个平面平行.

符号语言:α//β,m⊂β⇒m//α.

2个条件推出1个结论.面面平行⇒线面平行.

作用:证明直线与平面平行的的方法二(第二选择)

(6)线面垂直的判定定理

文字语言:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.

符号语言:l⊥a,l⊥b,a∩b=P,a⊂α,b⊂α⇒l⊥α.

5个条件推出1个结论,但是后面2个经常省略不写,“3个条件推出1个结论”即可.线线垂直⇒线面垂直.

作用:证明直线与平面垂直.

(7)线面垂直的性质定理一

文字语言:垂直于同一个平面的两条直线平行.

符号语言:a⊥α,b⊥α⇒a//b.

2个条件推出1个结论,线面垂直⇒线线平行.

作用:一个题目有“两条直线都和同一个平面垂直”的条件时,由此条件可以推出“线线平行”.

(8)线面垂直的性质定理二

文字语言:如果一条直线和一个平面垂直,那么这条直线和这个平面内的任意一条直线都垂直.

符号语言:a⊥α,b⊂α⇒a⊥b.

2个条件推出一个结论.线面垂直⇒线线垂直.

作用:(i)证明直线与直线垂直;(ii)一个题目有“线面垂直”的条件时,由此条件可以推出“线线垂直”.

(9)面面垂直的判定定理

文字语言:一个平面过另一个平面的垂线,则这两个平面垂直.

符号语言:l⊥β,l⊂α⇒α⊥β.

2个条件推出一个结论.线面垂直⇒面面垂直.

作用:证明两个平面垂直.

(10)面面垂直的性质定理

文字语言:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.

符号语言:α⊥β,α∩β=l,a⊂α,a⊥l⇒a⊥β.

4个条件推出一个结论.面面垂直⇒线面垂直.

作用:一个题目有“面面垂直”的条件时,由此条件可以推出“线面垂直”

在日常教学中,我要求学生必须熟记每个定理分别是“几个条件推出一个结论”,有的定理是“两个条件推出一个结论”,有的定理是“三个条件推出一个结论”,有的定理是“四个条件推出一个结论”,写证明过程的时候,不要“缺条件”.

我还经常在黑板上,对一些立体几何的证明题,写出完美的证明过程,起好的示范作用.

经过长时间的训练,学生对立体几何越来越感兴趣,数学成绩稳步提升.

在人民教育出版社出版的《数学必修2》课本的第66页的例2,原题如下:

例2如图2.3—9,在正方体ABCD−A1B1C1D1中,求直线A1B和平面A1B1CD所成的角.

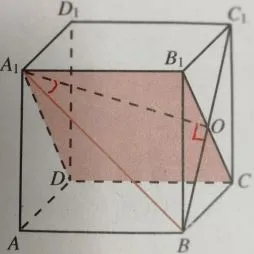
图2.3-9

解连接BC1交B1C于点O,连接A1O.设正方体的棱长为a,因为A1B1⊥B1C1,A1B1⊥B1B,所以A1B1⊥平面BCC1B1,所以A1B1⊥BC1,又因为BC1⊥B1C,所以BC1⊥平面A1B1CD,所以A1O为斜线A1B在平面A1B1CD内的射影,∠BA1O为A1B与平面A1B1CD所成的角.在Rt△A1BO中,因此,直线A1B和平面A1B1CD所成的角为30°.

对于课本给出的这个答案,证明过程严重“缺条件”,我建议将其修改完善如下:

解连接BC1,设BC1∩B1C=O,连接A1O.设正方体的棱长为a,

因为A1B1⊥B1C1,A1B1⊥B1B,B1C1∩B1B=B1,所以A1B1⊥平面BCC1B1.因为A1B1⊥平面BCC1B1,BC1⊂平面BCC1B1,所以A1B1⊥BC1.因为四边形BCC1B1是正方形,BC1、B1C是对角线,所以BC1⊥B1C.因为BC1⊥B1C,BC1⊥A1B1,B1C∩A1B1=B1,所以BC1⊥平面A1B1CD.因为A1B是平面A1B1CD的斜线,BC1⊥平面A1B1CD,所以A1O为斜线A1B在平面A1B1CD内的射影,∠BA1O为A1B与平面A1B1CD所成的角.因为BC1⊥平面A1B1CD,A1O⊂平面A1B1CD,所以BC1⊥A1O. 因为BC1⊥A1O,所以 ∠BOA1=90°,△BOA1为直角三角形,BA1=对于又因为∠BA1O是锐角,所以∠BA1O=30°,所以直线A1B和平面A1B1CD所成的角为30°.

在人民教育出版社出版的《数学必修2》第69页的例3,原题如下:

例3如图2.3-14,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A、B的任意一点,求证:平面PAC⊥平面PBC.

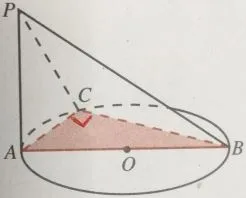
图2.3-14

证明设⊙O所在平面为α,由已知条件,PA⊥α,BC在α内,所以PA⊥BC.因为点C是圆周上不同于A、B的任意一点,AB是⊙O的直径,所以,∠BCA是直角,即BC⊥AC.又因为PA与AC是△PAC所在平面内的两条相交直线,所以,BC⊥平面PAC.又因为BC在平面PBC内,所以,平面PAC⊥平面PBC.

我建议将其修改完善如下:

证明设⊙O所在平面为α,因为PA⊥α,BC⊂α,所以PA⊥BC.因为AB是⊙O的直径,点C是圆周上不同于A、B的任意一点,所以 ∠ACB=90°.因为 ∠ACB=90°,所以BC⊥AC.因为BC⊥AC,BC⊥PA,AC∩PA=A,所以BC⊥平面PAC.因为BC⊥平面PAC,BC⊂平面PBC,所以平面PAC⊥平面PBC.