关于勾股数的思考与探索

江苏省苏州工业园区外国语学校(215021) 杨亚楠

勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方.勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例.

像3、4、5这样符合a2+b2=c2的正整数叫作勾股数又名毕氏三元数.勾股数就是可以构成一个直角三角形三边的一组正整数.笔者将以普林顿322为例来阐述勾股数的构造方法及普林顿322勾股数的构造方法.

问题背景:神秘的普林顿322

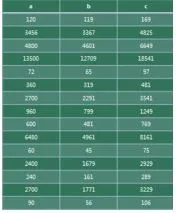
美国哥伦比亚大学普林斯顿收藏馆收藏了一块很古怪的泥板,这款泥板是在巴比伦挖掘出来的,编号322,考古学家相信这块泥板是公元前18世纪的成品,泥板上有三列文字,没有人能解释,直至1945年,Neugebauer和Sachs经过细心考究,发现泥板上是三列数字,你知道这些数字间的关系吗?借助计算器进行探索.

提出问题:如何构造勾股数?

透过验证我们发现a2+b2=c2,像这样的三个正整数,我们称为勾股数.我们常见的勾股数有3、4、5;5,12,13;7,24,25;8,15,17;9、40、41.如果a,b,c为一组勾股数,则na,nb,nc也是一组勾股数,其中n为自然数.例如3,4,5是一组勾股数,那么 6,8,10也是一组勾股数9,12,15也是一组勾股数.而普林顿322里面出现的较大的勾股数除去是常见的勾股数的倍数外,其他一些数据是怎么得来的呢?到底存在多少组勾股数呢?

问题解决:探寻“勾股数”

构造勾股数,就要寻找3个正整数,使它满足“两个数的平方和(或差)等于第三个数的平方”,既满足以下形式:()2+()2=()2或()2−()2=()2.我们可以从乘法公式的变形入手.我们知道:(x+y)2−(x−y)2=4xy.

(1)我们令x=m2,y=n2,上式即可写成:(m2+n2)2−(m2−n2)2=(2mn)2.于是,当m、n为正整数,且m＞n时,m2−n2,2mn,m2+n2就是勾股数.这就是著名的丢番图构造法!丢番图法我们发现,例如令m=2,n=1,得出一组勾股数为3,4,5;令m=3,n=2,得到一组勾股数5,12,13等.

(2)我们令x=n2,y=1,上式可以写成:(n2+1)2−(n2−1)2=(2n)2.于是,当n为正整数时,n2−1,2n,n2+1就是勾股数.这就是著名的柏拉图构造法.柏拉图法我们发现构造的勾股数,有两项相差2.至少一项为偶数.即c=a+2,b=2n.例如3,4,5;6,8,10;8,15,17等.

(3)我们令x=n2+2n+1,y=n2,上式可以写成:(n2+2n+1+n2)2−(n2+2n+1−n2)2=[2n(n+1)]2.于是,当n为正整数时,2n2+2n,2n+1,2n2+2n+1为勾股数.这就是著名的毕达哥拉斯构造法.毕达哥拉斯法我们发现毕达哥拉斯构造法所得的结果有一个特征,a是一个大于1的奇数,b,c为两个连续自然数,且有a2=b+c,则为一组勾股数.例如3、4、5是一组勾股数,且有32=4+5,5,12,13为一组勾股数,52=12+13,7,24,25为一组勾股数,72=24+25.

揭秘普林顿322

透过观察“普林顿322”上面的每排3个数据,我们发现后两个数的和除以2再开方刚好得到一个正整数(除第11排:60、45、90),因此符合丢番图构造法.