立足学生认知,回归教材起点*—从一道中考压轴题的溯源提数学复习的建议

贵州省贵州师范大学数学科学学院(550025) 邓清 夏小刚

在初中数学复习中,中考题对老师的复习有很好的导向作用,其中,中考压轴题更侧重考查学生对数学知识点深度综合和对数学思想方法的灵活运用.但部分教师由于对中考题压轴题的意图理解不透,导致在复习时容易脱离学生数学认知结构,在知识的综合复习部分简单安排为大量难题的机械训练,徒增学生学习负担.

数学认知结构是存在于学生头脑里的数学知识结构与认识结构有机结合而成的心理结构.而学生头脑里的数学知识结构又是课程教材里的知识结构和老师的数学知识结构在学生头脑里的反映[1].因此在对数学知识进行综合复习时,要立足于学生的数学认知结构,也就应注意回归教材,以教材为起点,引导学生进行思考分析,使问题的难点部分能在学生的原有认知结构中得到自然生长.下面笔者将结合贵阳市2015年的一道数学中考压轴题的溯源、引导学生的分析为例,谈谈对数学复习的思考与建议,供同行参考.

1.试题呈现与解评

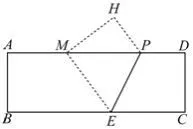
图1

题目(2015年贵阳中考卷第25题)如图1,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.

(1)求MP的值;

(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?

(3)若点G,Q是AB边上的两个动点,且不点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)

解析(1)利用矩形的性质和折叠的轴对称原理可知:在折叠纸片后,PD=PH=3,AB=CD=MH=4,∠H=∠D=90°,由勾股定理可得MP=5;

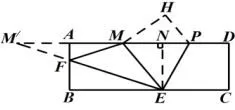
图2

(2)△MEF的周长为C△MEF=ME+MF+EF,由于ME的长为定值,因此只需求MF+EF的最小值即可.如图2,作点M关于AB的对称点M′,连接M′E交AB于点F,点F即为所求,且AM′=AM=4,过点E作EN⊥AD,垂足为N,由折叠可知:∠MEP=∠PEC,又根据 ∠MPE= ∠PEC,即可得 ∠MEP=∠MPE,即得ME=MP=5,在 Rt△ENM中,MN=又有NM′=NM+MA+AM′=3+4+4=11,由得所以当时,△MEF的周长最小;

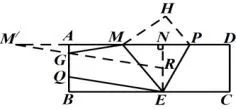
图3

(3)如图3,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ//RG,交AB于点Q,此时易得四边形ERGQ为平行四边形,即得GQ=ER=2,GR=QE,此时GM′+GR最小,且MG+QE=GM′+GR,则MG+EQ最小,四边形MEQG的周长最小,M′R=因为ME=5,GQ=2,所以,四边形MEQG的最小周长值是

评析起点低,落点高,思维难度层层递进是近年来贵阳市中考数学压轴题的命题趋势.本题以矩形折叠为背景,精巧地设置了动点求最值的两个递进问题,综合地考查了折叠和矩形的性质,勾股定理和相似三角形等相关知识,利用轴对称解决最短路径的转化思想.设置的三个小题,由易到难,层次分明.然而,笔者初探此题时,认为学生对第(3)问的处理难免感到突兀.学生即便由第(2)问想到利用轴对称将线段MG转换为M′G,依然很难求折线段M′—GQ—E的长度.如何引导学生较轻易地解决此问题呢?笔者将视线转移到学生的数学认知的映像之一——教材,并找到了此题的命题背景.

2.考题溯源

在贵阳市九年义务教育初中阶段使用的教材——北师大版八年级(下册)中具有这道题的模型,即教材90页第三章《图形的平移与旋转》的总复习题第18题,题目原型如下:

教材原题如图4,甲乙两个单位分别位于一条封闭式街道的两旁,现准备合作修建一座过街天桥.

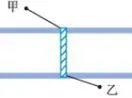
图4

①天桥建在何处才能使由甲到乙的路线最短?(注意:天桥必须与街道垂直).

②天桥建在何处才能使甲乙到天桥的距离相等?

这道题的思想方法与上述考题如出一辙,而且此题以生活情境为背景,更加形象直观,更能引起学生的兴趣.所以,笔者认为,如果教师在复习时引导学生对此题进行探究,并注重引发学生的操作与思考,从中提取数学本质,学生对这一中考题的解决会相对容易很多.因此,学生在第考题中(3)问犯难的时候,笔者打算先让学生回到教材中的这个题,并引导学生完成如下分析与思考:

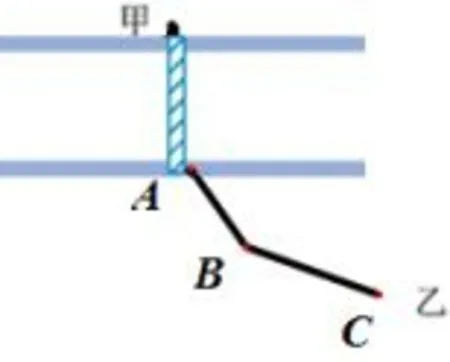
图5

问题分析与解决教材中这个问题的难点在于从甲到乙的路径必然是一条折线,也就是说要走的路径必然是三条线段长度之和.恰好就是天桥在中间拐一个弯,无法使路线在同一直线上,使其与学生原有的数学认知——“将军饮马”问题发生冲突,处理好这个冲突时解决问题的关键.继续引导学生发现,桥的位置并不会影响我们解决这个问题的思路,因此可以假设这样的特殊情况:假设桥就在单位甲或乙的位置,图5中以桥在单位甲位置为例.这样就把桥转化到路线的第一段,将变化的两条道平移到一起,就可以转化为“将军饮马问题”了.显然,当平移后的两条道AB、BC在同一直线上时,三条线段长度之和最短.

数学抽象引导学生将教材中过天桥的问题抽象出其数学本质,即求两个定点到一条可沿某一方向平移的定长线段两端距离之和最小问题,解决该问题的数学思想是借助平移与轴对称,把定点与线段端点的两条连线平移在一起,将所求折线段的长转化为将军饮马问题.如图6所示:经过转化后,即可将M′G+GQ+QE长度的最小值转化为M′G+GR+RE的最小值,显然,当M′、G、R三点共线时,M′G+GR+RE的值最小.

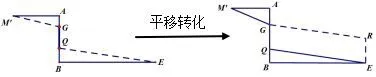
图6

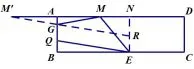
图7

回到考题引导学生掌握以上思想后,上述中考试题的第(3)问,学生只需借助轴对称,如图7,将线段MG转化为线段M′G,就成功地将四边形MGQE的周长转化为线段M′G+GR+RE的长,再借助勾股定理,问题的解决便显得顺理成章、水到渠成了.

3.归纳与拓展

在引导学生运用自己数学认知解决上述问题后,该模型由新知转化成了学生的已有数学认知,此时可继续引导学生将它与之前的认知建立联系,进行归纳与拓展,以形成结构化、体系化的数学思想方法.

归纳 (1)动点个数多于一个,且分别在两条直线上,求三角形最小周长.以图8为例,将定点进行两次轴对称转化,根据“两点之间,线段最短”,将△ABC周长转化为折线段A′B+BC+CA′的长,即可求得.

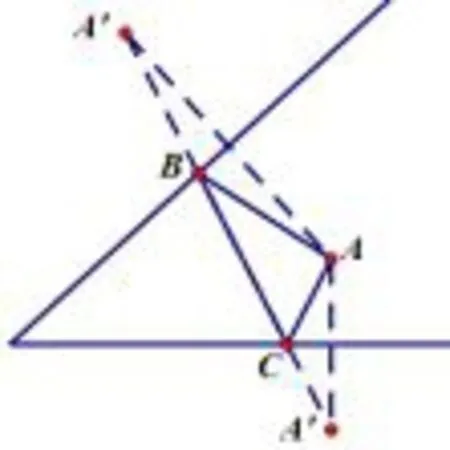
图8

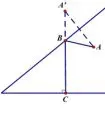
图9

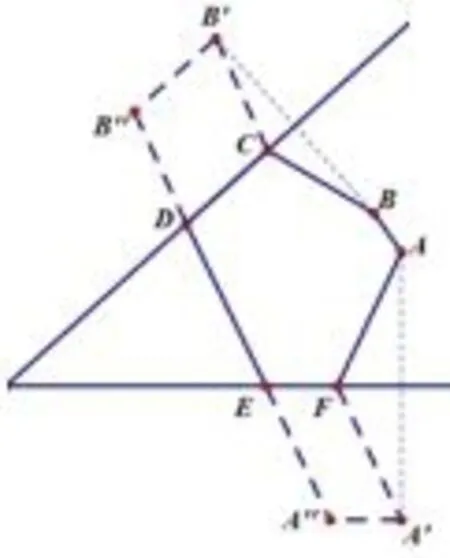
图10

(2)在(1)的情形下,若要求BC垂直某一条直线,求折线段AB+BC最小值时,以图9为例,将定点A进行一次轴对称转化后,将AB+BC的长转化为A′B+BC,根据“垂线段最短”,即可求得.

拓展若将该考题进行延伸,可以得到多条定长线段在多条直线上运动的问题,为了便于凸多边形的研究,在此仅推广为两条动线段的问题,如图10所示,将六边形ABCDEF的周长问题通过平移和轴对称转化为折线段的长,显然,当线段B′′D、DE、E′A三条线段共线时,六边形ABCDEF的周长最小.

4.总结及复习建议

学生的数学认知结构是数学知识和数学思想的加工厂,既为新知识的学习提供生长点或固着点,又为新知识的研究提供工具或方法[1].在向学生讲解上述压轴题时,笔者站在学生的认知角度去思考:在学生的数学认知结构中,有四边形最小周长问题的解决方法吗?如果没有,就将问题往学生数学认知结构转化,采用这种不断反思,逐步回归学生认知起点的思想,最终从教材中找到命题背景,以学生相对熟悉的情境,唤起学生的记忆,并引导学生逐步解决问题,再从中提取数学思想方法——平移和轴对称的转化法,让学生由直观到数学抽象,感悟问题数学本质,并进一步归纳和拓展,加深该模式在学生头脑中的印象.

中考试题通常都具有规范性、导向性、科学性等性质,每一道试题都凝聚着出题人的汗水和心血,特别是承担体现区分度的综合性试题,更是要经过命题人的千锤百炼[2],值得广大一线教师深入探测和研究.纵观各地历年数学中考压轴部分题目,大多取材都是源于课本,但又高于课本.为此,以教材为根基,借中考为导向,是中考数学复习的思想主线.下面,笔者从学生数学认知角度,谈谈对中考数学复习的一些建议,供同行参考.

(1)每节课的复习程序应注意立足学生数学认知,面向全体学生.在复习过程中,应注意从思想方法的重要程度和难易程度分层呈现,让所有学生有所收获.优秀的学生能力上得到提升,中等学生方法上有所启发,后进生在知识方面有所收获.

(2)知识回顾应系统化、结构化.复习时要切实用好课本,对课本内容必须做到全面复习,注重引导学生归纳、整理所学的知识点,建立合理的知识结构,挖掘知识内在联系,以便学生更好地感知教材、记忆教材.

(3)注意体会教材习题呈现的层次性.教材对较难思想方法的习题处理,总是根据学生的认知规律,按照层层递进,逐步上升的方法呈现给学生.教师要注意发现这一规律,引导学生学会把教材中一个较复杂的问题往认知起点回归,让学生体会思想方法的来源.

(4)习题的设计应具有典型性和阶梯性[3].习题设计时应体现教材的重要数学知识或重要数学思想方法,以教材中的典型例题和具有可生长性的习题为源,在此基础上进行延伸或变式.变式时应注意对题目的生长要自然,由易到难,由浅入深,如剥春笋,层层递进.

总之,中考数学试题立足于数学基础,符合课标要求,试题设计的本质都是教材中出现的基本内容、基本原理、基本方法和基本问题[4].中考数学的复习便应立足于学生的数学认知,从学生的数学认知出发,以教材为基础,以课标为导向,设计符合学生认知的复习方案.在综合性较强的习题讲解时必须贴近学生的思维水平,把握学生认知水平的最近发展区,安排好背景导入——最好是教材背景导入,把大题化小,难题化易,让每一位学生在在应对中考的同时,亦能得到各自较好的数学发展.