农村初中数学“题串”复习教法初探—以《反比例函数的复习》为例

广东省广州市增城区派潭镇第三中学(511385) 温秀梅

农村初中学生大部分是留守儿童,学习自觉性差,基础薄弱,对学习数学缺乏兴趣.而教师传统的课堂教学,调动不起学生学习的积极性.基于此,尝试运用广州市教学成果《三段六步》的理念,结合学生实际,对《三段六步》中的“以题点知”和“典型例题”进行精当改进,以《反比例函数复习》的局部教学设计与实施为例,探索农村初中数学“题串”复习教法,改进教学效果.

一、何谓“题串”复习教法

“题串”复习教法是在复习课上按照复习范围或复习专题内容,围绕一定目标或某一中心问题,按照一定逻辑结构而精心设计的一组问题串.教师根据复习内容设计相应的“题串”,开展问题式教学,引导学生在一系列问题中联系地、整体地复习,并发现问题的本质,结合“题串”解决相应问题.

二、“题串”教法的实施原则

(一)以题点知:同中求异以温故

在农村初中一般的复习课,往往都是通过建构知识结构图,以填空形式归纳整章书的定理公式、知识要点等,然后讲解一道例题,最后分层训练.复习的知识面较狭窄,复习效果并不明显,学生按照教师的教学思路按步就班,不利于培养学生的数学思维及创新能力.笔者在复习课尝试运用《三段六步》教学模式,收到一定的效果,但在课堂实施上,发现“以题点知”设计的5道不同小题把知识点摆了出来,但知识点之间是没有串联的,知识点像散落的星星,学生不会把它们“串”起来.教师在“以题点知”与“典型例题”环节之间找不到衔接点,使学生不会把“以题点知”的知识点解决“典型例题”,题型一变,难于找到解题方法与技巧.

于是对“以题点知”与“典型例题”进行了改进,5道小题是以同一题目呈现,设计不同的问题串,各题所呈现的知识点被串联起来,就像一串漂亮的珠链,不再是杂乱无章,而是问题层层深入.看似同一道题目,但每一道题又将本章的不同的核心知识要点以题目形式呈现出来,这样的设计,大大减低教学难度,更能激发学生的学习兴趣及学习自信心,从而达到同中求异以温故的效果.

1.题串设计呈现

1.下列图象中,是反比例函数的图象的是( )

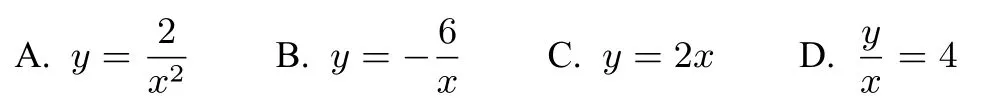
A. 第一、二象限 B. 第二、三象限

C. 第一、三象限 D. 第二、四象限

3.点(2,−3)是反比例函数的图象上的一点,则k=( )

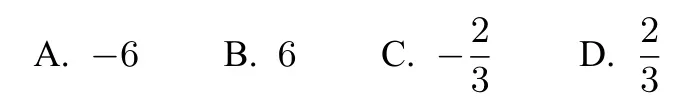
A.y1＜y2＜0 B.y1＞y2＞0

C.y2＜y1＜0 D.y2＞y1＞0

5.如图1,矩形ABOC的面积为6,反比例函数的图象过点A,则k=___.

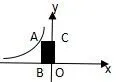
图1

2.设计意图解析

3.实施过程效果

在此环节实施中,先让学生独立思考,5分钟完成.之后教师呈现答案,以第4小题展开简单点评解题方法与技巧.教师提问:同学们,反比例函数的图象位于第二、四象限,在每个象限内,y随x的增大而增大,那么,对于反比例函数的图象和性质又是怎样的呢?学生已经对反比例函数的图象与性质已掌握,而对于反比例函数的图象与性质,学生很快就说出来了.通过5道以反比例函数解析式展开设计的练习,及教师提问反比例函数的图象与性质,把整节课要复习的核心知识,反比例函数的图象与性质,让学生轻松的掌握了.

设计题串,问题层层展开,同一道解析式,不同问题的设计,一步步地引导学生归纳总结,学生在练习中进一步深化本章的核心知识,加深巩固本章知识的联系,培养了学生独立思考,勇于探索的精神.当我们遇见熟悉的问题时,我们的心情是愉悦的,更让我们信心百倍地想去解决它.所以设计简单的题串更能激发学生学习的积极性,培养学生的发散思维,优化课堂结构,提高课堂效益.若是设计的题目不是题串,而是不同的题型展开,那么这样的设计对于农村薄弱学校的学生比较难接受,因为他们缺乏知识迁移的能力,知识储备少,对于含字母的解析式,比较抽象,没有感性认识,对于老师的直白讲解,很难参与到课堂中来,课堂效果大打折扣.

(二)典型例题:异中求同以知新

在大部分的复习课中,很多教师都是这样处理的,学生以填空形式完成本章的定理、公理或是公式,教师就摆出一道例题让学生解决.对于数学成绩好的同学,可能很快就解答出来.但在三分之一超过一半以上的薄弱学校,中下层学生缺乏学习热情,没有解题思路,无从下笔,于是学生就不愿意动脑思考了.而后三分之一面积太大,教师也照顾不了这么多学生,那么中下生只能等着教师来讲解.这样的课堂是失去活力的,长期以往,学生就会失去学习数学的信心,在数学课堂上就会趴倒一片.要打破这种课堂,要让全体学生动起来,积极参与到课堂中来,那么就必须激发学生学习数学的信心.在“以题点知”环节设计了简单的题串,以退为进,将知识点退到单一的知识层面上.当学生看到这么简单的题目,必然会被吸引住,他们就会迫不及待地想去做题.这样就可以调动起学生的学习积极性,树立起学生学习的信心,这样的课堂是多么有活力的课堂啊!为了让学生保持这种学习“兴奋性”,在设计的“典型例题”是继续以题串深入.这样两个环节就自然的衔接起来.有“以题点知”的核心知识作铺垫,解决“典型例题”就水到渠成了.

1.题串设计呈现

如图2,一次函数y=ax+b与反比例函数的图象交于A(−2,3),B(3,n)两点.

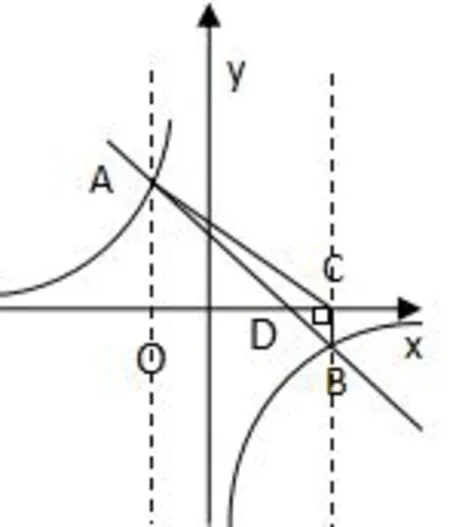
图2

(1)求一次函数与反比例函数的解析式;

(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

2.设计意图解析

例题设计是在“以题点知”的基础上继续深入学习,是对“以题点知”的核心知识的灵活应用.例题是在学生已掌握的反比例函数的图象与性质中以解答题的形式展开,看似不同的题型风格,其解决的方法与技巧如出一辙.这也是我们在教学课堂教学中需要培训学生的异中求同以知新的效果.

3.课堂实施效果

在教学上,先给学生独自审题思考,然后提问.

师:第1问求函数解析式,应该用我们所学过的什么方法来解决?

生:待定系数法.

师:你会先求哪个函数解析式?为什么?

生:先求反比例函数解析式.因为已知知道A点坐标,代入反比例函数解析式即可.

师:如果让你联系以题点知这五小题,应该对应哪题呢?

生:对应第3小题.

师:第2问求不等式的解集,我们能解答出来吗?

生:不能.

师:大家观察不等式左边ax+b与不等式右边其实是已知条件的什么式子?

生:(略思考)左边式子是一次函数的解析式的右边式子,右边式子是反比例函数右边的式子.题目求不等式的解集其实是求一次函数值大于反比例函数值.

师:能用第4题相同的方法来比较大小吗?如果不可以,你会用什么方法比较它们的大小?

生:不可以.因为第4题是比较同一函数函数值大小,而第(2)问的是比较两个不同函数的函数值大小,从图象去看,这两个函数一时一次函数在上面,一时反比例函数在上面,所以我们不能用第4题的方法来比较大小.我们应该用老师教的方法将图象分成两块四区(如上图)比较大小.先从y轴分为左右两块,y轴左边块过交点A作y轴平衡线一分为二两区,y轴右边块过交点B作y轴平衡线一分为二两区,然后再比较四个区的图象,看直线是否在上面,如果直线在上面,说明那么对应的x的取值就是所求不等式的解集.

全体学生:鼓掌!

对于第(3)小题是本节的一个难点,它与前面的“以题点知”没有相对应的知识点,为了突破这个难点,笔者在第(3)问设计了以下几个问题串,以达到降低教学难度,让我们大部分学生掌握解题方法与技巧.问题如下:

如图,一次函数y=ax+b与反比例函数的图象交于A(−2,3),B(3,n)两点.过点B作BC⊥x轴,垂足为C,

(1)在原题(1)的基础上求出一次函数y=ax+b与x轴y轴相交所形成的△EOF三角形面积?如图3-①所示.

(2)设一次函数y=ax+b与x轴交于点D,请你求出图3-②△ADC的面积.

(3)请你求出图3-③△BDC的面积.

(4)你能求出△ABC的面积了吗?

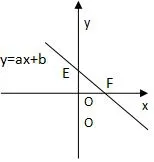
图3-①

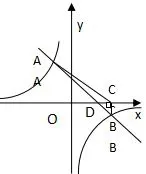
图3-②

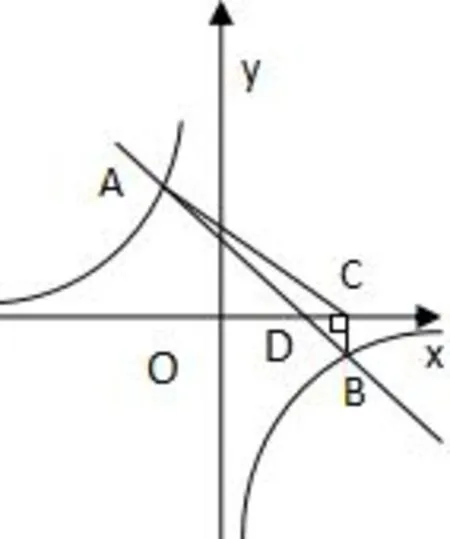
图3-③

这三个问题串的设计,是学生在已掌握求坐标三角形面积,到求有一边在坐标轴上的三角形面积,再到求三边都不在坐标轴上的三角形面积.“题串”设计逐步递进,从特殊到一般,教师把求三边不在坐标轴上的三角形面积通过转化成特殊有一边在坐标轴上的三角形面积来求.最后教师归纳这种题型的解题方法与技巧,让学生体验到了这种转化的数学思想.教学难点就迎刃而解了.

三、“题串”教法的教学启示

在复习课中,设计题串,大大调动了中下层学生学习的积极性,这节复习课取得意想不到的收获,受到以下教学启示.

(一)以题串点知,加深复习巩固效果

“以题点知”是以题串形式进行设计,让学生在不同的问题中,同中有异,异中有同,让学生在练习中潜移默化的训练中熟练掌握了反比例函数的核心知识,虽然函数解析式都是对反比例函数的一般式的性质不能全面表达出来,但在“以题点知”完成后,教师采取提问的方式提问的图象与性质.两者综合,归纳出了反比例函数一般式图象与性质,加深了学生对反比例函数的图象和性质的理解,达到了复习巩固提升的效果.

(二)题串“异中求同”,“同中辨异”

“题串”设计串联起整章书的知识结构,“阶梯性”设计,让全体学生得到不同发展,调动起中下层学生的学习激情,点燃了优等生的探究火焰.本节复习的重难点是教会学生如何利用反比例函数解决数学问题,例题的选取很有代表性.教师在处理重难点时,先让学生先尝试解答,师再设计问题串,与以题点知的5小题相呼应,让学生找出题串中的相似点与不同点,降低了学生解答例题的难度.教师在典型例题的引入时,先让学生独立思考完成,在限定时间内自主做题,为例题的学习起了铺垫作用,学生学习起来不费劲,容易理解.课堂上教师把五道小题与本例对应来学习,让知识之间串联起来,从而使复杂问题简单化,抽象问题形象化,学生更能掌握其内在联系.学生通过认真听讲,把教师对知识的高度抽象转化成自己对数学知识的理解.当学生展示完这道例题的解题过程后,师再小结概括解题思路.概括是课堂教学的核心环节,而串联是一种概括方式,是以教师为中心,把新、旧知识和学生之间不同认知经验串联起来,特别是把学生通过感官获得的操作性直接经验和通过内隐思考获得的反思性经验串联,以“异中求同”来抓住问题的本质和共性,以“同中辨异”来区分问题的形式和个性.题串的设计不仅在复习课堂上有效,在我们的新授课、练习课中同样可用.例如在新授课讲授等腰三角形的性质时,也可以设计题串来学习.

等腰三角形三线合一性质的题串设计:

1、已知:AB=AC,∠1= ∠2,求证:AD⊥BC,BD=DC.(提示:利用全等证明)

2、已知:AB=AC,AD⊥BC,求证:∠1= ∠2,BD=DC.

3、已知:AB=AC,BD=DC,求证:AD⊥BC,∠1=∠2.

以上三道小题的练习中,我们得到等腰三角形的另一性质(“三线合一”)

等腰三角形的___角平分线,____边上的中线,____边上的高互相重合.

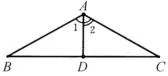
图4

(三)课内批改,个别指点

达标训练的习题是针对前面所复习的知识内容再现,练习设计分层,让不同层次学生得到不同的发展.以题点知是以题串形式展开对本章知识点的再现,是“同中求异”,而达标训练的练习是对学生前面所复习内容的巩固提升,习题设计必须是多方面的、多角度、多样式来考察学生的应变能力.是前面所说的“异中求同”.此环节教师也是要求学生限时完成,教师穿梭各小组中批改作业,个别指点,然后针对学生的易错题和难题重点讲解,并归纳题型的通用解法,加深了学生对知识点的理解,提高了复习的有效性.

此外,笔者在最后利用了极算子大数据库设计了题串式的过关检测环节,当堂检查学生对本章知识的掌握情况.5分钟的限时检测,教师马上总结出本章知识,哪些学生掌握较好,哪些是学生的薄弱环节,需要教师在下一阶段作出教学的调整.大大提高了教学效率.

四、结语

从设计到实施,“题串”的设计由单一知识点、由浅入深、由现象到本质的递进层次进行设计,这种阶梯式的教育模式,优化了课堂效率,提高了复习课的有效性.题串式的教学,重在教师对题串的“设计”,把问题设计在最原始最基本的层面上,把中下层学生的学习激情调动起来,把优等生的数学思维激活,让全体学生“动”起来,这就是我们需要的课堂.