基于“名师引领”的数学教学—青年教师成长的捷径

广东省珠海市第七中学(519000) 于 焱

广东省珠海市南屏中学(519000) 刘建海

青年教师在成长过程中“走弯路”是难免的,有的人在走完后琢磨明白了,就促进了自身水平的提升.但实际情况中不允许每位老师都通过“走弯路”然后幡然醒悟而有所提升,所以师父的引领是重要的,名师工作室的引领,更是青年教师成长的捷径.过去有拳谚说“宁传十口,不摸一手”.“口”是“你要怎么样”是要达成的目标,“手”是“你可以这样”是达成目标的方法,可见师父经验的宝贵.郑板桥在诗歌《新竹》中写道“新竹高于旧竹枝,全凭老干为扶持.”更是指出青年教师要成长甚至想在前辈的基础上有所发展,离不开师父的引领.我非常荣幸参加珠海市于焱中学数学名师工作室,在于焱老师的引领下、在众多优秀同伴学员的指导激励下我收获良多.现我把在工作室中看到的名师关注点、参与活动所得的浅薄收获跟大家分享,让大家参考、吸取经验、尽量少走弯路.

图1

教师的主阵地在课堂,要想上好课先要备好课.于焱老师在谈到课堂教学时多次强调:课堂需要遵循入门易、讲解透、训练熟三个原则.要想做到入门易就离不开研究学情.美国图画大师李欧·李奥尼在绘本《鱼就是鱼》里描述了这样一个故事:有一条鱼和一条蝌蚪是池塘里的一对好朋友,后来小蝌蚪变成青蛙后离开了池塘.某天,青蛙回到池塘向小鱼描述外面的世界,于是就出现了如图1中的画面:鱼“学到”的牛是只具备“牛”特点和“鱼”身的怪物.这跟学情——鱼的原有知识密切相关.可见,学情对课堂教学的效果有重大影响.

建构主义学习理论认为:学生在学习新知识时是通过已有的知识结构同化吸收的,在原有知识与新知识之间存在一个最近发展区,教师要成为学生建构意义的帮助者,就要在教学过程中创设符合教学内容要求的情境和提示新旧知识之间联系的线索,帮助学生建构当前所学知识的意义.可以认为:学生的原有知识能顺利同化新知时就觉得“易”,否则就是“难”.所以,要想实现入门易,研究学情是不可少的.新课程标准的实施建议——教学建议强调:数学知识的教学,要注重知识的“生长点”与“延伸点”,把每堂课的知识置于整体知识的体系中,注重知识的结构和体系,处理好局部知识与整体知识的关系,引导学生感受数学的整体性,体会对于某些数学知识可以从不同的角度加以分析、从不同的层次进行理解.由此可知,教师对学情研究的重要性.

如在进行平方根的教学时可以根据学情,类比学生学过的绝对值的知识进行新课引入:

1.利用数轴回答以下问题:

(1)数轴上距离原点2.5单位长度的数是___;

(2)若|a|=5,则a=___;

(3)若|a|=0,则a=____;

(4)是否存在数a使得|a|=−5?答____.

2.62=___,(−6)2=___,132=___,(−12)2=____,02=____,( )2=−4.

结论:任意一个有理数a的平方___0(填 ≥、＞、≤)

要想实现讲解透就得在备课中重点突出,直指核心问题,让学生有醍醐灌顶的顿悟感觉.教科培中心的毕东宁老师说:备课时,先找到这节课最核心的问题,然后围绕它组织教学活动,层层铺垫解决.如在进行《9.3一元一次不等式组》的教学时,于焱数学名师工作室成员——五中韩彬老师是这样处理的:韩彬老师没有向课本那样直接教学生解课本例题:(1)而是通过分析,学生已经掌握了解不等式的方法,而不等式组先要解两个不等式,然后把两个不等式的解集在数轴上描述出来并找出两个解集的公共部分,从而写出不等式组的解集.因此本节课的核心问题是如何把找出两个解集的公共部分,只需解决这一点,则新知就完全可以转化为已学知识来同化、建构.所以韩彬老师先通过四组简单的不等式组如让学生通过画数轴找公共部分,掌握如何找不等式组的解集.然后再抛出课本例题,只需稍作点拨,则学生就显得轻车熟路了.

当核心问题解决后,课堂需要进行适当的练习,让学生把所学知识在灵活运用的过程中形成能力,也就是——训练熟.于焱老师在培训时强调:习题或检测,要明确每一个(组)习题或练习的设计目的,加强检测的针对性、有效性.注意防止一步到位,过早给综合题、难题有害无益;基础不够的题目更是贻害无穷——题目出不好是老师专业素养低的表现之一.在一次我上完公开课后于焱老师指导我说:其实你不需要配那么多习题,留几个有针对性和代表性的就够了.我恍然大悟,以后在备课时常常想到这一幕.

图2

然而“适当”是一个很难把握的度,平时我很注意参考各类教参、教辅材料,当看到各种各样的“好题”时,难免会着相一个“贪”字,不懂得“取舍”,总想每个“好题”都让学生练、都讲.现实是时间不允许,一节课的教学任务完成不了,课时不够.效果也不好,不少题目虽然给学生练习过,但再次出现还是不会做,甚至连印象都没有.这迫使我思考:课堂讲得多、练得多效果就真的好?有一幅漫画(图2)形象的反映了“多”与“少”的关系,也形象的诠释了老子说的“少则得、多则惑”的道理.学习又何尝不是如此!教师一节课中不停的狂轰乱炸,学生真正留下的不一定多,涓涓细流式的积累不一定就是少.“少”不是无原则的少,而是少而精——典型,少而专——透彻,老师就更会注意所选练习的典型与针对性.

教科培中心李东涛老师谈到练习的设计时也多次强调:习题的选择要注意四个方面:层次、典型、变式、归一.

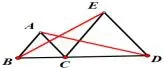
图3

其中的“层次”对应着“入门易”,“典型”需要分析知识目标.而“变式”是非常值得我们花功夫去研究的,课堂教学过程中如果注意变式教学,不仅有利于提高课堂效率,也有利于帮助学生在拓展思维的同时建立完成知识结构,从而实现“归一”的原则.如在上等边三角形时经常会遇到这个问题:如图3,已知,点B、C、D三点共线,等边△ABC、等边△CDE,求证AD=BE.针对这个问题,可以从广度与深度两方面进行变式.深度方面:

变式1:如图4、图5,把图形进行向里或向外旋转,问题不变;

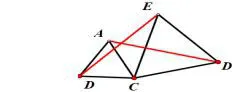
图4

图5

变式2:如图6、图7,把图形旋转到特殊位置,问题不变;

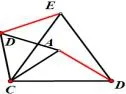
图6

图7

变式3:如图8,增加交点M、N,求证图中的三对全等三角形;

变式4:如图9,连接MN,求证三角形MCN为等边三角形;

变式5:如图10,连接CP,求证CP是∠BPD的角平分线;

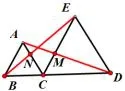
图8

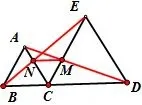
图9

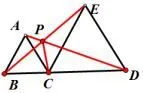
图10

变式6:如图11,增加AD、BE的中点P、Q,求∠CPQ的度数;

变式7:如图12,若AQ=BP,求∠CPQ的度数;

变式8:把基本图形放在坐标系中,如图13,三角形ABC为等边三角形,E是x轴上任意一点,以CE为边作等边三角形CEF,连接FB并延长与y轴交于点G,求证点G为定点.

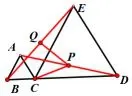
图11

图12

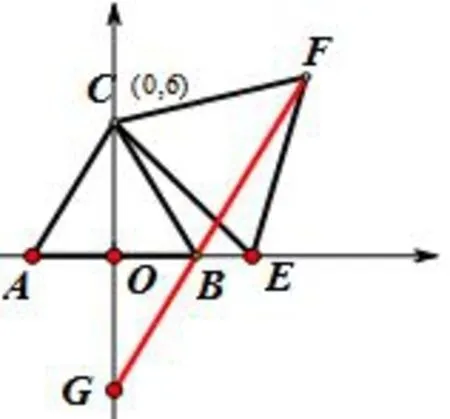
图13

广度方面,可以继续类比变式,如:

变式9:如图14,分别以三角形ABC的两边AB、AC为边作等边三角形,求证CD=BE;变式10:如图15,分别以三角形ABC的两边AB、AC,为边作等腰直角三角形,求证CD=BE;

变式11:如图16,分别以三角形ABC的两边AB、AC,为边作正方形,求证CD=BE;

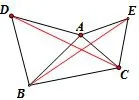
图14

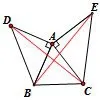
图15

图16

教学过程中开展变式的同时,注重引导学生进行知识的归一,如从不同的题目中归纳出相同的模型:如图17,在三角形ABC中,∠ABC=30°,AB=3,BC=5,△ACD是等边三角形,求BD的长.可以引导学生参考图14的基本图形进行补形(图18)从而解决问题.

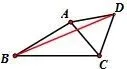
图17

图18

最后,用紫荆中学桃园校区邹军主任课堂寄语来总结:每节课教学目标要突出,发挥聚焦作用,每节课上课内容力求能给学生留下深刻印象(核心问题).教学需根据学情,以学定教,教学内容要有梯度,善用题组训练(学情、层次、变式).