不经历“过程”怎么得“结果”
广东省中山市板芙镇第一中学(528459) 韦秋梅
心理学研究表明:不经历学生个人亲身探索和发展的过程,要想把已知的真理变成学生的真知是不可能的.《义务教育数学课程标准(2011年版)》指出:学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.因此,在教学实践中,教师要引导学生主动体验知识形成和发展的过程.
一、要经历数学概念的形成过程
从题目特点可以看出,这5个小题出得并非偶然,而是老师刻意而为之的,是老师在对教材的深刻理解和对学生已有水平有着正确的预见基础上循序渐进的整合,每道题都恰到好处地设置障碍,遵循学生认知.引导学生从类比互逆中得出概念,很好地让学生明白新知识“怎么来?”“为什么要学?”使得平方根的概念不再是来得“唐突、冷冰冰的”,而是“自然”的,有“温度”的.整个学习过程不断地让学生体会着“柳暗花明又一村”的学习快乐.
人们对新事物的认知与接受需要有一个过程.数学概念是数学知识体系中的基本元素,是从客观世界中直接或间接抽象出来的,具有一定的抽象性.因此,教学中应注意基于学生已建构的知识体系和认知经验,引导学生通过观察、分析、比较,找出共性,理解概念.
案例1平方根概念
新课的引入:两数相加得和,而若已知和与其中一个加数,要求另一个加数,就得由加法运算引出减法运算,减法运算得到的结果称为两数的差;两数相乘得积,而若已知积与其中一个因数,要求另一个因数,就得由乘法运算引出除法运算,除法运算得到的结果称为两数的商;我们之前学习了乘方运算,如32=9,3是底数,2是指数,32叫幂,结果为9,而若已知幂和指数,如何求底数呢?我们得引入一个新的运算,开2次方根(开平方),如此类推,也有开3次方根,开4次方根等,我们今天先研究开平方,我们把开平方运算得到的结果称为平方根或二次方根.
接着老师安排以下这道练习:下列各数的平方根分别是多少?
二、要经历数学定理的探索过程
数学定理是前人证明成立的结论.在教学中,教师要引导学生积极参与定理的发现过程,经历与前人发现数学定理大致相同的思维过程,不断满足学生的探索欲望,培养他们善于思考的数学品质.
案例2探索勾股定理
问题:观察图1,三个正方形A,B,C的面积有什么关系?
追问1:由这三个正方形A,B,C的边长构成的等腰直角三角形三条边长度之间有怎样的特殊关系?
追问2:观察图2,在网格中的一般的直角三角形,以它的三边为边长的三个正方形A,B,C是否也有类似的面积关系?
追问3:正方形A,B,C所围成的直角三角形三条边之间有怎样的特殊关系?
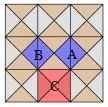
图1

图2
把相应正方形的面积表示为相应边长的平方,再把等腰直角三角形抽出来,可发现面积的数量关系可转化为等腰直角三角形三边之间的关系.然后让学生探究一般的直角三角形,看看是否仍有相同的数量关系.教学时引导学生用割补法,观察计算出结果.最后,引导学生在方格纸上画出一个直角三角形及以三边作为边长的正方形,通过小组之间的合作交流,发现是否也有相同的数量关系,进而表示为式子.这种转化过程对学生来说是有难度的,不能操之过急.在学生计算出面积结果后,引导学生观察总结出来,即使学生表述不太准确都没问题,切不可忽略探索过程而把结论硬塞给学生.
课堂上教师结合毕达哥拉斯的传说故事,引导学生从特殊到一般探索发现勾股定理,整节课都在探索思考的跌宕起伏中进行,相信经过这一曲折的探索过程得到的结论,给学生留下的印象定会历久弥新的.另外,在探索学习的过程中,学生经历了从数学的角度观察事物、思考问题,体会“数学源于生活,并服务于生活”.
三、要经历数学难点的细分过程
在教学中,教材对某个知识点的阐述和编排往往与教学实践操作存在着一定的距离.这些知识点恰恰羁绊着学生学习新知的脚步,也就是常说的难点.教师需巧设教学,引领学生细化难点,逐一突破.
案例3画正比例函数y=2x的图象
描点法画函数图象的一般步骤:列表、描点、连线.“连线”要求是:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.学生在用描点法画正比例函数图象时,出现了两种状况,第一种情况是预习了教材上的内容,描完点后直接用直尺画出一条直线,发现所描的点中有点不在这条直线上也置之不理.第二种情况是严格按照描点法画图象的要求,把所描出的各点用平滑曲线连接起来,由于所描的点有限,误差较大,连成的图象歪歪扭扭像条小蚯蚓,与课本上的图象大相径庭,这就引起了学生的认知冲突,哪里出了问题?然而课本恰恰没有提及.此时,教师引导学生采用“逐步细分”的方法在点(0,0)与(1,2)之间找出10、20……等分点,并同时利用计算机软件画出图象的这一段,在这个过程中,让学生体验随着坐标点的不断增加,正比例函数图象逐渐趋于一条直线.
学生经历这样的探索过程是非常必要的,对后续函数的学习有着重要的启发作用,同时也培养了学生善于发现问题和提出问题的能力,意义深远.
四、要经历数学解题的思考过程
数学永远离不开解题.在进行解题教学中,先给予充分的时间让学生独立思考,再结合小组合作讨论的方式进行探讨,最后通过“听、讲、评”的过程充分暴露学生的思考过程,同时,在不断优化和逐步深入的解题过程中,培养学生积极思考、善于聆听、勇于表达的数学学习习惯.
案例4人教版八年级下册数学教材第50页练习5
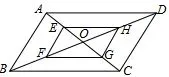
图3
如图3,平行四边形ABCD的对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点.求证:四边形EFGH是平行四边形.
在结合图形仔细分析已知条件,综合运用了中位线定理和平行四边形的性质、判定定理,经过一番思考与讨论后,学生的思路如下:
思路1:证两组对边分别相等;
思路2:证两组对边分别平行;
思路3:证两条对角线互相平分;
思路4:证一组对边平行且相等;
思路5:证两组对角分别相等.
最后,由学生一起对5种思路进行评析,前4种思路分别从不同的角度得出结论,各有优势,相比之下,第5种思路较为复杂.这道题的解答过程并不是“唯做题而做题”,而是深挖题目的价值,引导学生主动思考,善于观察分析.在学生思维碰撞的过程中沟通了知识之间的内在联系,提高了学生的解题水平,优化了思维品质,培养了学习信心.
有些老师认为:重视过程的教学需要耗费大量的课堂时间,会造成后面的教学任务无法完成,有些结论不需要引导学生证明,只要学生记住定理,会做题就行了.而笔者认为,长此以往,学生可能学会了高效获取知识,却不会思考,更谈不上创造,因为“直奔结果”的学习方式使得知识的获取过程缺乏思想方法的领悟和活动经验的积累.学生接受新知是一个循序渐进的过程,我们不能带着一份“功利求快”的心理对待课堂.在教学过程中,有些教学内容老师本身觉得很简单,上课是一带而过或者直接告诉结果,掩盖了学生的疑问和想法,其实教师的体验和理解永远代替不了学生的体验和理解.在教学中,我们把握好教学的方向,当好教学的组织者,大胆地把学生推到前面,舍得放手让学生自己体验,有了“过程”的厚重,必然会有“结果”的丰满.

